Индуктивность, емкость и сопротивление в цепи переменного тока.

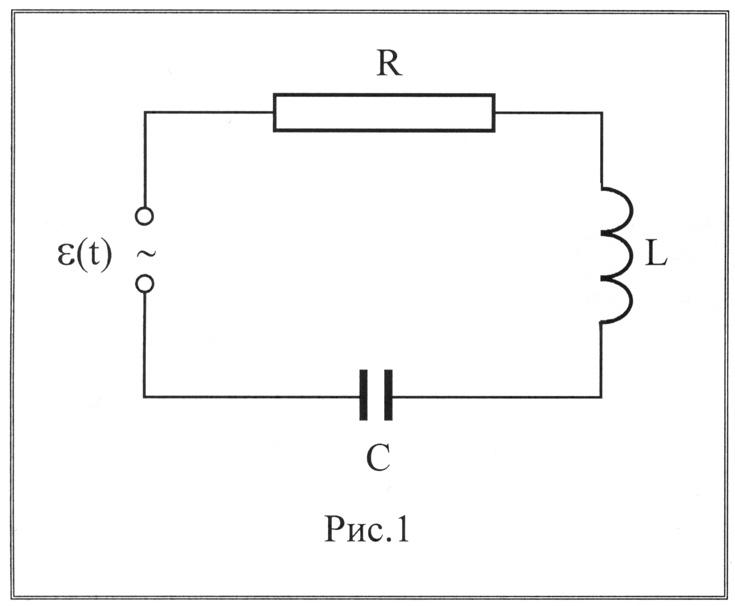
Рассмотрим электрическую цепь, состоящую из сопротивления R, катушки индуктивностиL, и конденсатора емкостьюC, к которым приложена внешняя ЭДС, изменяющаяся со временемε(t). Согласно закону Ома для данной цепи можно записать:

(8)

где I– сила тока,

R– сопротивление, ,(_o– максимальное значение внешней ЭДС,ω– частота колебаний),Учитывая, что и, выражение (8) можно записать в виде:

. (9)

Это дифференциальное уравнение второго порядка описывает вынужденные колебания с учетом сопротивления. Решая это уравнение, получаем выражение для амплитудного значения силы тока:

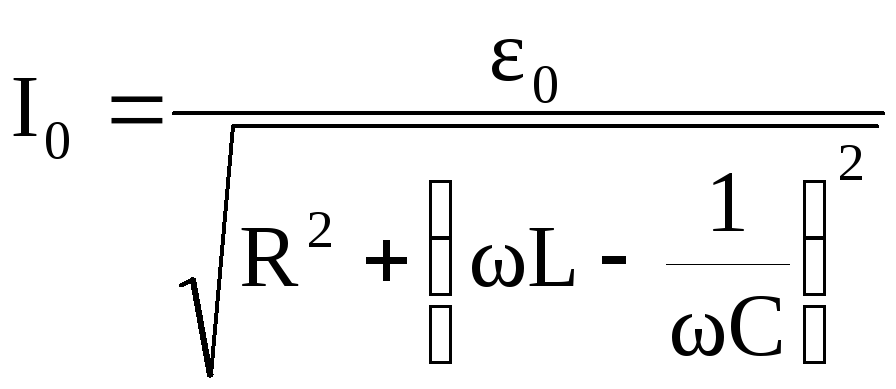(10)

Выражение (10) можно рассматривать как закон Ома для переменного тока.

В этом случае

– полное сопротивление цепи переменного тока,R– омическое сопротивление,ωL– индуктивное

4

сопротивление, – емкостное сопротивление, величину– часто называют реактивным сопротивлением. В случае если в цепи переменного тока отсутствует либо катушка индуктивности, либо конденсатор, выражение (10) упрощается, т.к. в этом случае либоR_L =ωL, либо равны нулю.

Схема установки

Рассмотрим электрическую цепь, собранную согласно рис.2, где P

п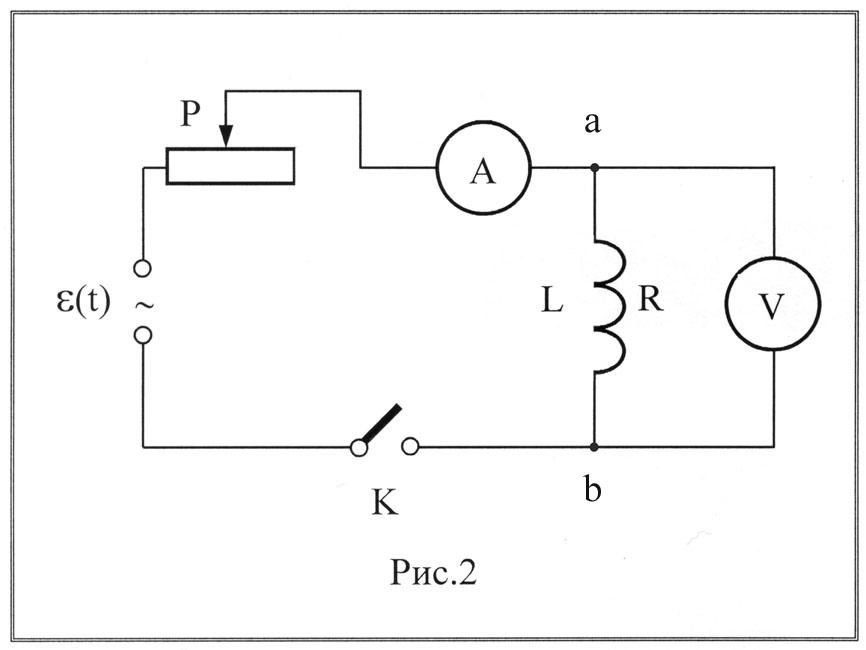олзунковый реостат;

L– соленоид с омическим

cопротивлением R;

А – амперметр,

V– вольтметр, К – ключ.

Для нахождения неизвестного значения индуктивности Lможно использовать закон Ома для участка цепиab: , (11)

где I₀ и U₀ – амплитудные значения силы тока и напряжения на участкеab,R– омическое сопротивление соленоида,R_L=ωLиндуктивное сопротивление соленоида. Приборы переменного тока измеряют эффективные значения силы тока и напряжения, которые связаны с амплитудными значениями следующим образом:

и

(под эффективным значением, например, силы переменного тока, понимают такую величину постоянного тока, который в омическом сопротивлении выделяет ту же мощность, что и переменный ток). Учитывая вышесказанное, формулу (11) можно записать в следующем виде:

(12)

Найдя с помощью приборов I_эф. иU_эф. Можно определить полное сопротивление участка цепиab:

(13)

5

Так как , то зная омическое сопротивлениеR, можно найти индуктивность соленоидаL:

(14)

Здесь = 6,2850 Гц = 314 Гц.

Порядок выполнения работы

1. Собрать цепь по схеме рис.2.

2. Определить цену деления амперметра и вольтметра.

3. Вынув сердечник из катушки, включить ключ «К».

4. Изменяя ползунковым реостатом ток в цепи, измерить I_эф. иU_эф. Измерения выполнить для пяти значений токов и напряжений. Результаты измерений занести в таблицу 1.

Примечание.Амперметр и вольтметр регистрируют эффективные значения тока и напряжения  I_эф.и U_эф..

Таблица 1.

№	Iэф А	Uэф В	Z Ом	L Гн	Lср. Гн	ΔL Гн	ΔLср. Гн
1.
2.
3.
4.
5.
Омическое сопротивлениеR=					 =

5. Занести в таблицу 1 и таблицу 2 значение сопротивления соленоида R.

6. Вставить ферромагнитный сердечник в катушку. Измерить U_эфпри заданном преподавателем значенииI_эф.

7. Выдвигая сердечник из катушки каждый раз на 2 см и поддерживая ползунковым реостатом заданное значение I_эф, найти соответствующие значенияU_эффдо полного удаления сердечника из катушки. Результаты измерений занести в таблицу 2.

6

Таблица 2.

№	Iэф. А	l см	Uэф. В	Z Ом	L Гн
1.		16
2.		14
3.		12
4.		10
5.		8
6.		6
7.		4
8.		2
9.		0
Омическое сопротивлениеR=			 =

Примечание:l(см) – часть сердечника, находящаяся в катушке.

Обработка результатов измерений

1. Пользуясь формулой (13), рассчитать полное сопротивление для каждого измерения и данные занести в таблицу 1.

2. Рассчитать значения индуктивности соленоида по формуле (14) для каждого измерения и данные занести в таблицу 1.

3. Рассчитать среднее значение индуктивности соленоида 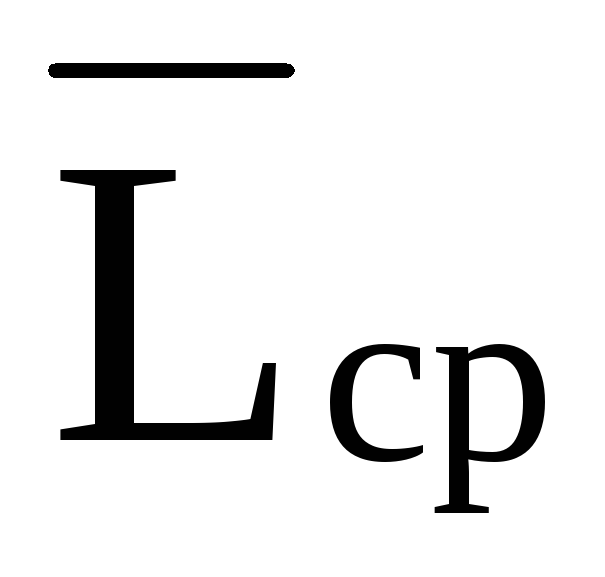, абсолютные погрешности измерения , среднюю абсолютную погрешность , и относительную погрешность . Все рассчитанные величины записать в таблицу 1.

4. Повторить расчеты, указанные в п. 1 и 2, используя данные таблицы 2.

5. Построить график зависимости индуктивности соленоида Lот глубины погруженияlсердечника в катушку.

7