Энтропия и информация. Критерии оптимальности

4.7. Количество информации как критерий степени организованности системы. Вместо термина «неопределенность» можно использовать понятие неупорядоченность, разнообразие, хаос (см.п.4.4.). Тогда вместо определения «устраненная неопределенность» можно употребить термин «блокированное разнообразие».

В кибернетике биологом и кибернетиком Эшби [26] был сформулирован закон «необходимого разнообразия»:

«каждая система, блокирующая разнообразие, должна иметь собственное разнообразие, не менее блокированного.»

Или короче – «только разнообразие может уничтожить другое разнообразие».

Эта почти философская трактовка проводит очень простой принцип. Процесс с возрастанием энтропии происходит самопроизвольно. Например, для того чтобы на базе составов выходных потоков ректификационной колонны получить состав входного потока достаточно смешать продуктовые потоки и диффузионный процесс смешения пойдет «сам собой».

Другое дело обратный процесс – процесс разделения. Он происходит с понижением энтропии и для его осуществления требуется некоторая организация процесса, например, наличие специальных установок – ректификационных колонн определенной сложности. Степень организованности такой системы и предлагается оценивать на основе устраненной системой неупорядоченности или количеством блокированного разнообразия.

Критерий оценки степени организованности системы в общем виде записывается как отношение

,

где , – энтропия, оценивающая неупорядоченность потоков на входе и выходе любой системы.

В термодинамической интерпретации для разделительной системы этот критерий есть отношение термодинамически минимальной работы разделения исходной смеси на заданные продукты к аналогичной работе разделения на абсолютно чистые продукты.

Поскольку разность в числителе есть количество информации, то этот критерий можно рассматривать также как информационный

.

Для ректификации согласно (4.12)

,

и

,

тогда

. (4.24)

С помощью этого критерия удобно оценивать разделительную способность (разделительную мощность) колонны, – чем больше разность , т.е. количество информации, тем выше разделительная способность колонны и тем выше качество разделения.

Критерий (4.24) нормирован на единицу. Максимально возможная разделительная способность соответствует и . Тогда и . Это отвечает гипотетическому случаю, когда колонна делит бинарную смесь на чистые продукты или многокомпонентную смесь на две чистые фракции. Практически такой режим недостижим, так как требуется колонна с неограниченным числом ступеней разделения. Наоборот, когда процесс сводится к простому делению смеси на два потока исходного состава, то и .

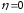Выражение (4.24) применяется как критерий оптимальности в задачах оптимизации процессов разделения (см. п.5.4). При этом критерий (4.24) используется как относительная оценка качества разделения.

В общем случае число выходных потоков из системы может быть любым. Естественно добиваться максимального значения критерия для действующей колонны. Если величина при этом фиксирована (состав питания задан), то максимизация сводится к минимизации энтропии выходных потоков. Таким образом, в задачах оптимизации с фиксированной энтропией входных потоков реализуется принцип м и н и м а л ь н о й энтропии.

Следует обратить внимание на разнообразие функций, выполняемых энтропией. Так, в предыдущем разделе, где речь шла о моделировании процессов, использовался прямо противоположный принцип – м а к с и м а л ь н о й энтропии.

При моделировании процессов (см. в п.3.7) о познавательных моделях) мы пытаемся как бы «подстроиться» под природу, которая при прочих равных условиях предпочитает состояния с максимальной энтропией. Но максимум энтропии это и максимум беспорядка, поэтому при проектировании систем мы стараемся там, где это возможно, уменьшить максимум. В этом смысле энтропия в инженерных задачах носит как бы м и н и м а к с н ы й характер.

5. КРИТЕРИАЛЬНЫЙ ВЫБОР

АЛЬТЕРНАТИВНЫХ РЕШЕНИЙ

5.1. Постановка задачи оптимизации. Одной из особенностей инженерных задач является многовариантность инженерных решений. Поясним это на примере проектного расчета кожухотрубного теплообменника. Пусть на основе соответствующего математического описания рассчитана требуемая поверхность теплообмена – F. В ходе расчета поверхности теплообмена был выбран также диаметр трубок – d. Теперь задача заключается в конструктивной реализации поверхности – F, т.е. выборе числа и длины трубок – n и l в соответствии с геометрией F=dln. Поскольку в этом выражении фиксированы только параметры F и d, то один параметр из двух оставшихся (l, n.) оказывается свободным.

Это означает, что требуемая поверхность теплообмена может быть конструктивно реализована различным способом, многими вариантами. Все варианты в одинаковой степени работоспособны и таким образом соответствуют поставленной цели. Воспользуемся теперь системным понятием эффективности системы. Эффективность есть качество достижения цели, т.е. указание на то, с какими затратами достигнута цель (см. п.2.2). Под затратами можно понимать разные оценки. Например, качество достижения цели можно измерять в данном примере металлоемкостью конструкции. В этом случае принято говорить, что металлоемкость выступает в качестве критерия оптимальности (Р) для выбора лучшего, или оптимального варианта. На рис.5.1 представлен характер зависимости критерия оптимальности от числа трубок в теплообменнике. Оптимальное число трубок n = n_opt соответствует минимальному значению критерия Р.

Критерий оптимальности часто называют также целевой функцией или функцией выгоды.

В данном примере участвует один независимый свободный, или варьируемый параметр (n или l.). Число варьируемых параметров определяет порядок, или размерность задачи оптимизации.

Таким образом, оптимальным значением параметра называем такое его значение, при котором некоторая функция, играющая роль критерия оптимальности, достигает экстремального значения (максимума или минимума).

Различие между строго научным (системным) пониманием оптимальности и «общежитейским» толкованием заключается в том, что в строгой системной постановке термин «оптимальный» предполагает наличие критерия оптимальности.

Задачи оптимизации отличаются по постановке от обычных задач только наличием блока критерия оптимальности. Выбор критериев диктуется особенностью задачи. Далее рассматриваются основные типы критериев оптимальности.

5.2. Экономические критерии оптимальности. На примере ректификационной установки рассмотрим, как появляется необходимость в специальном критерии оптимальности экономического характера. Пусть требуется разделить исходную смесь на два продукта (дистиллят и кубовый остаток). Свойство ректификационной системы таково, что одну и ту же степень разделения можно достичь различными способами. В частности, возможен вариант с достаточно большим числом массообменных ступеней разделения (массообменных тарелок – N), но с малой подачей пара в куб колонны – Q (рис.5.2, вар.1). Возможны и другие варианты: с малым числом тарелок, но значительными затратами пара (рис.5.2, вар.2).

Выражаясь языком системного аналитика можно сказать, что цель систем одинакова, а качество достижения цели, т.е. их эффективность различна. Каким образом оценить эффективность этих вариантов? Для этого необходимо иметь в виду, что число массообменных ступеней разделения связано с разовыми, капитальными затратами (руб.), а расход пара – с постоянными эксплуатационными затратами (руб./ед. времени).

При общей оценке необходимо сложить эти два типа затрат, приведя их к одной размерности. Эту функцию выполняет экономический критерий приведенных затрат (Р)

Р = С + ЕК/В,

где С – себестоимость, руб./ед. прод.

К – капитальные затраты, руб.

В – производительность, ед. прод./год.

Е – нормативный коэффициент эффективности капитальных вложений, Е = 0.15 1/год. Обратная величина этого коэффициента соответствует нормативному сроку окупаемости капитальных вложений.

Экономический критерий приведенных затрат достаточно часто используется в практике проектирования, разрешая компромисс между капитальными и эксплуатационными затратами (см. рис.5.2).

В задачах оптимального управления, в которых капитальные затраты фиксированы, в качестве критерия оптимальности может использоваться прибыль.

Пр = В(Ц – С),

где Ц – цена продукции, руб./ед. прод.

Экономические критерии являются наиболее общими: они учитывают как капитальные, так и эксплуатационные затраты. Их недостаток – требование большого количества надежной информации о текущем состоянии рынка.

5.3. Термодинамические критерии оптимальности. Термодинамические критерии в отличие от экономических оценивают энергетическое совершенство систем. При этом такая оценка производится на фундаментальной термодинамической основе. Чаще всего для этой цели применяется термодинамический КПД системы, как отношение двух работ

 = А_о/А, (5.1)

где А_о – термодинамически минимальная работа для осуществления заданного процесса; А – фактически затрачиваемая работа.

Например, для только что рассмотренного процесса разделения.

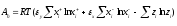
Cледует обратить внимание, что в термодинамическом критерии (5.1) используется отношение работ, а не энергий вообще. Но в реальных системах происходят процессы с затратой как работы, так и тепла. Для термодинамически корректного перехода от тепловой энергии к механической в современной инженерной практике используется понятие эксергии (Е). Эксергия теплоты – работоспособная энергия, максимальное количество механической энергии, которое можно получить из тепловой энергии Q c температурой Т при стандартной температуре окружающей среды Т_о=298 К

Е = Q(1- (T_о/T), где Т  Т₀

Нетрудно заметить, что в скобках стоит КПД цикла Карно.

Выражение для минимальной работы разделения относится к любому процессу разделения, а не только к ректификации. Например, сравнительно низкое значение термодинамического КПД для ректификации, несколько процентов, указывает на несовершенство этого способа разделения в принципе. Не случайно природные системы, которые не могут обходиться без разделительных процессов, тем не менее, не используют принципы ректификации, а «изобрели» процесс разделения с помощью мембран. Для мембранного разделения термодинамический КПД на порядок выше. Широкомасштабному внедрению мембранной техники в промышленную практику препятствуют пока высокие капитальные затраты.

Термодинамический КПД, как было указано, оценивает энергетическое совершенство системы и не учитывает капитальных затрат. Предпринимались попытки ввести термоэкономические критерии, но они не получили достаточного распространения.

5.4. Информационный критерий оптимальности. В качестве информационного критерия оптимальности может быть использован рассмотренный ранее критерий оценки степени организованности системы (см.п 4.7). Особенность использования этого критерия вновь продемонстрируем на типовой системе химической техники – ректификации.

Критерий оценки степени организованности системы (4.24), который для процессов разделения имеет смысл показателя, оценивающего качество разделения, позволяет сгруппировать основные режимные и конструктивные параметры процесса ректификации в две группы. Для уяснения сущности такого деления рассмотрим характер зависимости критерия (4.24) от основных режимных и конструктивных параметров, характеризующих процесс ректификации: N – число теоретических тарелок; R – флегмовое число; – относительный отбор верхнего (нижнего) продукта; – параметр, характеризующий место ввода питания в колонну. Здесь – число теоретических тарелок в верхней секции колонны. Таким образом. рассматривается зависимость

при варьировании одного из параметров и фиксированных значениях остальных. На рис.5.4 представлен характер этих зависимостей.

Из рис.5.4 а, б следует, что с повышением числа ступеней разделения и флегмового числа степень организованности системы (мощность разделения) возрастает. Это достаточно тривиальный результат, поскольку он констатирует, что мощность разделения можно увеличить, если прибегнуть к дополнительным капитальным затратам (увеличить число массообменных тарелок) или к дополнительным эксплуатационным затратам (увеличить флегмовое число за счет подачи тепла в кипятильник ректификационной колонны). Такой путь повышения степени организованности системы называется экстенсивным, т.е. затратным.

Совсем другой характер имеет зависимость критерия оценки степени организованности системы от параметров и (рис.5.4 в). Эти зависимости носят экстремальный характер. Они получены при фиксированных значениях «затратных» параметров N и R. Таким образом, существует такое место ввода питания в колонну (), а также такое значение отбора продукта (, либо ) при мощности

а)

б)

в)



Рис.5.4. Влияние режимных и конструктивных параметров процесса ректификации на информационный критерий степени организованности системы

разделения. Такой путь повышения степени организованности системы можно назвать интенсивным.

С физической точки зрения дополнительная мощность разделения достигается за счет «внутренней экономии процесса», например, за счет лучшего распределения движущих сил по высоте колонны.

Итак, основные режимные и конструктивные параметры процесса ректификации можно разделить на две группы:

• интенсивные параметры, варьирование которыми приводит к повышению организованности системы при неизменных затратах;

• экстенсивные параметры, варьирование которыми также приводит к повышению организованности системы, но за счёт дополнительных капитальных или эксплуатационных затрат.

Прибегая к популярной форме изложения особенностей информации, этот результат возможно истолковать иначе, можно сказать, что если вы обмениваетесь с коллегой каким-либо предметом, то в результате обмена у каждого останется по одному предмету, Если же в таком обмене участвует не предмет, а некоторая идея (информация), то в результате обмена у каждого становится по две идеи. Если вещество и энергию можно израсходовать, то информацию можно передавать без опасения, что её у вас станет меньше. Можно считать, что положительный эффект в случае в (рис. 5. 4 ) достигнут за счет информации, т.е. знания того, где находится самое лучшее (оптимальное) место ввода питания или каково оптимальное значение отбора продукта.

Одним словом, одну и ту же цель, например, повышение качества разделения, можно достигнуть разными го достигать цели за счет информации, т.е. подбором соответствующих значений интенсивных параметров.

Этот вывод носит самый общий характер. Так сегодня говорят о единстве вещества, энергии и информации, но более целесообразно достигать нужной цели в производстве не за счет вовлечения всё большего количества сырья и энергии, а продвигаться к ней за счёт освоения новых технологий, т.е. за счет информации.

5.5. Системность критериев оптимальности. Иногда приходится иметь дело с несколькими критериями оптимальности, принимая для каждого иерархического уровня свой критерий. В этом случае может возникнуть проблема системности критериев, т.е. согласованности их между собой.

Рассмотрим типичный случай из области химической техники. При разработке новых массообменных элементов (тарелок) для разделительных систем возникает необходимость ввести оценку их эффективности. Руководствуясь здравым смыслом можно считать массообменный элемент тем эффективнее, чем выше его интенсивность и ниже гидравлическое сопротивление элемента (Р). Интенсивность процесса массообмена обычно измеряют « КПД массообменной тарелки» (), как отношение числа теоретических тарелок к реальным = n_о/n.Тогда можно ввести составной критерий, оценивающий эффективность массообменного элемента в виде следующего отношения:

 = /Р

Рассмотрим, каким образом можно проверить системность (согласованность) этого критерия с критерием экономического характера и при этом одновременно уяснить само понятие системности. Поступим следующим образом. Сравним две ректификационные колонны с эквивалентными целями – равными разделительными способностями, т.е. равным числом теоретических тарелок. Пусть колонны оборудованы разными массообменными элементами, но с одинаковыми значениями критерия , т.е. ₁ =₂,

где ₁ = ₁/Р₁; ₂ = ₂/Р₂ при ₂=2₁, Р₂ = 2Р₁

Если сравниваемые колонны с одинаковыми локальными критериями  будут равны и по затратам, то критерий назовем системным, т.е. согласованным с критерием более высокого иерархического уровня.

Проделанные несложные оценки параметров двух ректификационных колонн приведены в табл.5.1. Разделительная способность колонн оценивалась фиксированным числом теоретических ступеней разделения (теоретических тарелок). Из приведенных оценок можно сделать следующий вывод. Ректификационная колонна, оборудованная тарелками второго типа, требует их в два раза меньше при одинаковом общем гидравлическом сопротивлении сравниваемых колонн. Это означает, что колонна второго типа имеет существенно меньшую металлоемкость (меньшие капитальные затраты) при практически одинаковых энергетических затратах. Следовательно, критерий  не системен с экономическим критерием, поскольку первоначально на основе критерия  ошибочно предсказывалась эквивалентность сравниваемых конструкций колонн.

Составной критерий типа  иногда используется для сравнения эффективности массообменных устройств. Он вводится на основе здравого смысла, который, как видим, иногда может подводить.

Как указывалось, системы обладают только им присущими, интегративными свойствами. Это затрудняет получение строго системных локальных критериев. Тем не менее существуют специальные методы редуцирования локальных критериев на основе критерия приведенных затрат [27].

Следует обратить внимание, что введенный в п.4.7 информационный критерий для оценки степени организованности системы является примером строгого системного локального критерия оптимальности. Свойство локальности здесь проявляется в подчиненности критерию при оптимизации только интенсивных свободных переменных.

Таблица 5.1.

К проверке системности критериев

Характеристики колонны	Первый вариант	Второй вариант
Число реальных тарелок	n1=N/1	n2=N/2= N/21=n1/2
Общее гидравлическое сопротивление	P1=n1Р1	P2=n2Р2=(n1/2)2= =Р1= P1

5.6. О методах оптимизации. Наиболее простой способ поиска оптимального решения – обычный перебор с выбором наилучшего варианта. На первый взгляд кажется, что возможности современных компьютеров вполне позволяют это сделать. Произведем предварительную оценку такой возможности. На рис.5.5 представлена схема из четырех последовательно соединенных реакторов с рециклами.

T₁

T₂

T₃

T₄

r₁

r₂

r₃

r₄

Рис.5.5. Система из четырех последовательно соединенных реакторов с рециклами

Требуется найти простым перебором оптимальные значения четырех относительных рециклов r и четырех температур Т. Таким образом, в такой задаче восемь свободных переменных. Упростим задачу и будем считать, что область оптимальных температур для каждого реактора известна с точностью до 10 ^ градусов требуется лишь уточнить ее до одного градуса. Таким образом, требуется перебрать 10 значений температур для каждого реактора. 10 различных значений примем также для относительных рециклов. Тогда общее число вариантов расчета составит 10 ⁸.

Примем, что один вариант расчета системы реакторов с определением значения целевой функции составляет 0,1с. Тогда время расчета всех вариантов составит 0,110⁸с. В году примерно 310⁷с и, следовательно, расчет займет около трети года – четыре месяца (!)

Неслучайно среди специалистов, занятых оптимизацией, существует даже специфическое ругательство - «проклятье размерностью». Действительно, даже невысокая размерность (в примере – восемь) при столь грубом решении (проверялось всего 10 вариантов по каждому из 8 параметров) дает столь неприемлемый вариант для продолжительности расчета! Вот почему вместе с развитием вычислительной техники происходил прогресс в совершенствовании математических методов поиска оптимальных решений.

Математические методы оптимизации относятся к классу условных экстремальных задач. Внешне эти методы отличаются от постановки обычных школьных задач поиска экстремума функции лишь тем, что здесь экстремум отыскивается при некоторых ограничениях, условиях. Такими ограничениями в этих задачах служат уравнения математической модели системы. Примеры таких ограничений уже фигурировали ранее, см. выражения (4.21) - (4.23).

Все методы оптимизации можно разделить на две группы: аналитические и численные.

Для относительно небольшой части инженерных задач, к которым применимы аналитические решения, наиболее часто для оптимизации применяется метод неопределенных множителей Лагранжа (см.п.4.6). Сущность метода уже рассматривалась и заключается в использовании функции Лагранжа, которая позволяет перевести задачу из класса условных экстремальных задач в класс обычных безусловных, метод решения которых хорошо известен.

Большинство задач оптимизации сводится к численным методам. Различают задачи линейного и нелинейного программирования.

К линейному программированию относятся задачи оптимизации, в которых как независимые уравнения математической модели объекта, так и выражение для критерия оптимальности являются линейными функциями.

Пусть математическая модель содержит n независимых линейных уравнений, которые включают в себя m режимных и конструктивных параметров: x₁, x₂, …x_m. В задачах оптимизации mn, а разность k =m – n определяет число свободных, варьируемых параметров. Если из числа m зафиксировать любые k параметров, принятых в качестве свободных, то систему уравнений можно разрешить однозначно. Решения, в которых свободные переменные приравниваются нулю, а другие переменные из m параметров принимают неотрицательные значения называются базисными решениями. Исходная система уравнений имеет ограниченное множество базисных решений. Например, при m=4, k=2 существуют следующие шесть базисных решений: х₁=0, х₂=0; х₁=0, х₃=0; х₁=0, х₄=0; х₂=0, х₃=0; х₂=0, х₄=0 и х₃=0, х₄=0.

Доказано, что оптимальное решение в задачах линейного программирования надо искать среди базисных решений. Поиск происходит путем перебора всех базисных решений и выбора из них одного с экстремальным значением критерия оптимальности.

К задачам линейного программирования сводятся многие задачи оптимизации в экономике.

Методы поиска оптимальных решений в общем случае (нелинейное программирование) подробно рассматриваются в курсе прикладной математики. Напомним, что сюда относятся метод Гаусса – Зейделя и множество вариантов градиентных методов.

Некоторую специфику составляет метод динамического программирования (метод Беллмана [28]), разработанный специально для оптимизации последовательно соединенных объектов, (см. рис.5.5). Метод основан на оптимальной стратегии, которая достаточно очевидна: «каково бы не было начальное решение, последующее должно быть оптимальным относительно состояния, возникшего в результате первого решения .