Сбалансированные и идеально сбалансированные деревья. Деревья поиска
Дерево идеально сбалансировано, если для каждого его узла количество узлов в левом и правом поддереве различается не более чем на 1.
Дерево сбалансировано, если для каждого его узла высота двух соответствующих поддеревьев различается не более чем на 1.
Дерево поиска- дерево, в котором для каждой вершины
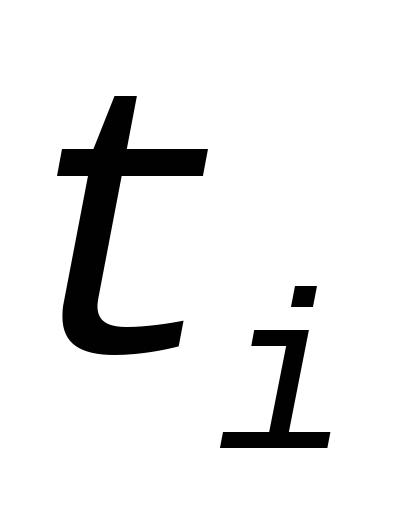справедливо утверждение, что все ключи
ее левого поддерева меньше ключа
,
а правого - больше ключа
.
Поиск в таком дереве может проходить
только по единственному пути.AVL-дерево(Адельсон-Вельский, Ландис) – сбалансированное дерево поиска.
Рис. 6. Примеры двоичных деревьев.
а), b) - сбалансированные деревья; b) - идеально сбалансированное дерево, дерево поиска, AVL-дерево
СОЗДАНИЕ ИДЕАЛЬНО СБАЛАНСИРОВАННОГО ДЕРЕВА
Последовательность шагов при создании идеально сбалансированного дерева для заранее известного числа вершин (n):
Создается корневая вершина;
Тем же способом строится левое поддерево, содержащее nl=n div 2 вершин;
Тем же способом строится правое поддерево, содержащее nr=n-nl-1 вершин;
Рекурсия завершается, если поддерево не содержит ни одной вершины (n=0).
ПРИМЕР 3.ПРОЦЕДУРА СОЗДАНИЯ ИДЕАЛЬНО СБАЛАНСИРОВАННОГО ДЕРЕВА
Type
Tree=^Node;
Node=Record
Key:Char;
Left,Right:tree;
end;
Var
n:Integer;
Root:Tree;
{Процедура распечатки дерева, повернутого на 900 против часовой стрелки (см. также пример 1), обход ПКЛ}
procedure PrintTree(t:tree;n:integer);
begin
if t<>nil then
with t^ do
begin
PrintTree(Right,n+1);
Write('':4*n);
Writeln(key);
PrintTree(left,n+1);
End;
end;
{Cоздание сбалансированного дерева с N узлами}
Function CreateTree(n:Integer):tree;
var
newnode:tree;
nl,nr:integer;
x:char;
begin
if n=0 then Createtree:=nil
else
begin
nl:=n div 2; nr:=n-nl-1;
Write('Введите значение:');
Readln(x);
new(newnode);
with newnode^ do
begin
key:=x;
left:=Createtree(nl);
right:= Createtree(nr);
end;
Createtree:=newnode;
end;
end;
{ Тело программы }
Begin
Write('Введите число узлов:');
Readln(n);
root:=CreateTree(n);
Writeln ('Создано дерево:');
PrintTree(Root,0);
End.
ПРИМЕР 4. Нарисовать диаграмму идеально сбалансированного бинарного дерева, при КЛП-обходе которого будет получена последовательность ключей, составляющих слово ЭНЕРГИЯ. Вывести результат для ЛПК и ЛКП обходов. Указать высоту и длину пути дерева.
…
ДОБАВЛЕНИЕ УЗЛА В ДЕРЕВО ПОИСКА (поиск с включением)
АЛГОРИТМ ПОСТРОЕНИЯ ДЕРЕВА ПОИСКА
В дереве поискаищется узел с заданным значением (x). Если узел найден, то выводится сообщение, в противном случае в соответствующую позицию добавляется новый узел.
ПРИМЕР 5. НАРИСОВАТЬ ДИАГРАММУДЕРЕВА ПОИСКАДЛЯ ПОСЛЕДОВАТЕЛЬНОСТИ КЛЮЧЕЙ, СОСТАВЛЯЮЩИХ СЛОВОАПРЕЛЬ. ВЫВЕСТИ РЕЗУЛЬТАТЫ ТРЕХ ОБХОДОВ ПОЛУЧЕННОГО ДЕРЕВА. УКАЗАТЬ ВЫСОТУ И ДЛИНУ ПУТИ ДЕРЕВА.
РЕШЕНИЕ:
Рис. 8. Иллюстрация к примеру 5
ОБХОДЫ:
Корень-Левое-Правое (КЛП): АПЕЛРЬ
Левое-Корень-Правое (ЛКП): АЕЛПРЬ
Левое-Правое-Корень (ЛПК): ЛЕЬРПА
Высота (корень на уровне 0): 3
Длина пути: 11 =0+1+2*2+3*2
Программную реализацию построения дерева с такими свойствами см. в примерах 7-8
ПРИМЕР 6. ПОИСК ЗАДАННОГО ЗНАЧЕНИЯ В ДЕРЕВЕ ПОИСКА
Function Locate (x:Integer; t:Tree):Tree;
Begin
While (t<>nil)and(t^.key<>x) do
if t^.key<x then t:=t^.right
else t:= t^.left
Locate:=t
End;
Если возвращается Nil, то узел не найден.
Вариант использования барьера при поиске в дереве поиска см. на стр. 247
См. также 681.3 В52 Вирт Н. Алгоритмы и структуры данных. - СПб.: Невский диалект, 2001,стр.246-247 (в т.ч. вариант использованиябарьерапри поиске).
ПРИМЕР 7.ПРОЦЕДУРА ПОИСКА С ВКЛЮЧЕНИЕМ (рекурсивный вариант)
procedure Search(x:char; var p:tree);
begin
if p=Nil then
begin
new(p);
with p^ do
begin
Key:=x;
Left:=nil;
Right:=nil;
end
end
else
if (x<p^.Key) then Search(x,p^.Left) else
if (x>p^.Key) then Search(x,p^.Right)
else Writeln('Узел существует')
end;
Для рекурсивной процедуры поиска значения в дереве достаточно заменить блок включения нового узла на вывод сообщения (или возврат значения nil), а вывод сообщения 'Узел существует' можно оставить (или заменить ссылкой на найденный узел).
Использование деревьев поиска для сортировки данных - строим дерево поиска, после чего обходим его по правилу ЛКП (по возрастанию) или ПКЛ (по убыванию)
ПРИМЕР 8.ПРОЦЕДУРА ПОИСКА С ВКЛЮЧЕНИЕМ (без рекурсии)…
ЗАДАНИЕ 2. Нарисуйте деревья, которые будут созданы функцией CreateTree (пример 3) и процедурой Search (пример 7) для вводимой последовательности символов "ИНФОРМАТИКА".
ПРИМЕЧАНИЕ. См. также программы: TreeSearch.exe (каталог \Программы\02_ДеревоПоиска) - создание дерева поиска и его обход; Demt.exe (каталог \Программы\03_ДеревоПоиска) - создание дерева поиска и его балансировка.
УДАЛЕНИЕ УЗЛА ИЗ ДЕРЕВА ПОИСКА
ПРИМЕР 10. ПРОЦЕДУРА УДАЛЕНИЯ УЗЛА ИЗ ДЕРЕВА ПОИСКА
Замечание:При удалении элемента с двумя потомками происходит его замещение на самый правый элемент левого поддерева (см. процедуруdel)
Более подробно см.681.3 В52 Вирт Н. Алгоритмы и структуры данных, 2001, стр. 255-258.
PROCEDURE DELNODE(x:char; VAR p:tree);
var q:tree;
procedure del(var r:tree);
{Используется только в случае, когда удаляемая вершина имеет двух потомков}
begin
if r^.right<>nil then del(r^.right) else
begin
q^.key:=r^.key;
q:=r;
r:=r^.left;
end;
end;
begin
if p=nil then writeln('Узел отсутствует') {узел не найден}
else
if x<p^.key then DELNODE(x,p^.left) { ищем x в левом поддереве}
else if x>p^.key then DELNODE(x,p^.right) { ищем x в правом поддереве)
else {delete p^}
begin
q:=p; {устанавливаем ссылку q на найденный узел p}
if q^.right=nil then p:=q^.left else
if q^.left=nil then p:=q^.right else del(q^.left);
dispose(q)
end;
end;
КОММЕНТАРИИ
Если хотя бы одно из поддеревьев P пусто, устанавливаем ссылку P с вершины-предка на оставшееся поддерево (VAR в заголовке процедуры Delnode!!!).
Если оба поддерева содержат узлы, то используем процедуру del - отыскиваем наибольшую вершину в левом поддереве (R^), она имеет нулевую правую ссылку, перемещаем ее ключ в вершину Q^, переносим ссылку Q на вершину R^ и после этого удаляем именно крайнюю правую вершину в левом поддереве (а не исходную найденную вершину с двумя ссылками).
ЗАДАНИЕ 4. Проиллюстрируйте на конкретном примере пп.1-2 комментариев.
