2 Классическая вероятность. Вероятности событий в опытах с конечным числом исходов

Любое случайное событие А, которое может произойти в опыте, может рассматриваться как подмножество из элементарных событий некоторого пространства Ω элементарных событий. Само пространство Ω отождествляется с любым событием, которое всегда наступает в опыте и называется достоверным. Пустое подмножество пространства Ω отождествляется с любым событием, которое никогда не наступает в рассматриваемом опыте. Это событие называется невозможным и обозначается символом .

Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта или вероятность случайного события - это численная мера степени объективной возможности наступления этого события.

Существует несколько методов определения вероятностей событий.

Пусть Ω = { ₁; w₂ ; ... w_n } - некоторое пространство элементарных событий соответствующих какому-то эксперименту. Каждому элементу w_i из Ω поставим в соответствие неотрицательное число p_i так, что p₁+p₂+...+p_n=1. Выбор чисел p_i происходит, как правило, исходя из сравнения возможностей различных исходов эксперимента. Число p_i называется вероятностью элементарного события w_i . Вероятностью любого события А называют число Р(А), равное сумме вероятностей элементарных событий, составляющих А. При этом, если событие А не содержит элементов, то вероятность Р( А ) = 0.

Пример 2.1 Из карточек разрезной азбуки составлено слово “математика”. Затем из карточек наугад выбирается одна. Рассмотрим пространство элементарных событий Ω= {а ; м ; т ; е ; к ; и }, где, например, элемент “и” означает, что выбрана карточка с буквой “и”. Обозначим через P() вероятность элементарного события . Тогда целесообразно определить вероятности элементарных событий в этом опыте следующим образом: P(a)=0.3, P(м)=P(т)=0.2, P(е)=P(к)=P(и)=0.1. Действительно, возможность выбрать карточку с буквой “а” в три раза превышает возможность выбрать карточку с буквой “е”. Очевидно, P(а)+P(м)+P(т)+P(е)+P(к)+P(и)=1. Тогда, если событие А - выбрана карточка с гласной буквой, то вероятность Р(А)=P(а)+P(е)+P(и)=0.3+0.1+0.1=0.5.

Предположим, что по условиям опыта все элементарные события равновозможные, то есть каждое элементарное событие не имеет никаких преимуществ в появлении по сравнению с остальными элементарными событиями (то есть при большом количестве опытов все исходы наблюдаются с одинаковой частотой). Тогда имеет смысл считать, что р(w₁)=р(w₂)=...=р(w_n) и, следовательно, р(w_i )=.

Обозначим через - число элементов конечного множестваА. Если событие А содержит k элементарных событий, то

P(А)=.. (2.1)

Исходы, при которых происходит некоторое событие называютсяблагоприятными или благоприятствующими событию

Тогда вероятность события по формуле (2.1) определяется как отношение числа благоприятных исходов к числу всех возможных.

Это определение вероятности события называется классическим.

Пример 2.2. Игральной костью называют выполненный из однородного материала кубик, грани которого помечены номерами 1; 2; 3; 4; 5; 6 так, что сумма чисел на противоположных гранях равна семи.

Игральная кость подбрасывается один раз. Пространство элементарных событий Ω = { 1; 2; 3; 4; 5; 6 } , где, например, элементарное событие 1 означает, что кость упала гранью с номером 1 вверху. Описание опыта позволяет считать все элементарные события в пространстве Ω равновозможными из-за симметричности игральной кости. Поэтому целесообразно полагать равными вероятности всех элементарных событий, то есть P(1)=P(2)=...=P(6)=.

Пусть событие А - на верхней грани игральной кости выпал четный номер. Тогда А={2; 4; 6 } и Р(А)=. Пусть событиеВ - на верхней грани игральной кости выпало простое число. Тогда В={1; 2; 3; 5} и Р(В)= .

Для вычисления вероятности по классическому определению необходимо находить число элементов в пространстве элементарных событий Ω и в различных случайных событиях - подмножествах A . Это часто удается сделать, используя комбинаторные методы. Большинство комбинаторных задач решается с помощью следующих двух основных принципов.

Принцип умножения. Если множество А содержит n элементов, а множество В содержит k элементов, то множество всех различных упорядоченных пар вида (a;b), где содержитnk элементов.

Пример 2.3. Из города К в город L можно попасть через город F и G, не соединенные между собой дорогой. Пусть из города К в город F ведут 4 разные дороги, из города F в город L ведут 2 разные дороги, из города К в город G ведут 2 разные дороги и из города G в город L ведут 3 разные дороги.

Каким числом различных путей можно совершить путешествие из города К в город L через города F и G ?

По принципу умножения число различных путей из города К в город L через город F равно 4^. 2=8, а число различных путей из города К в город L через город G равно 2^. 3=6. Следовательно, число различных путей из города К в город L через города F или G по принципу сложения равно 8+6=14.

Принцип сложения. Если множество С можно разбить на два непересекающихся подмножества А и В, множество А содержит n элементов, множество В содержит k элементов, то множество содержитn+k элементов.

Множество, состоящее из n элементов, будем называть упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число (номер элемента) от 1 до n. Упорядоченные множества считаются различными, если они отличаются друг от друга либо некоторыми элементами, либо их порядком, то есть номерами. При этом элемент с меньшим номером называется предшествующим элементу с большим номером.

Упорядоченные k-элементные подмножества из n элементов называются размещениями из n элементов по k. Число различных размещений из n элементов по k обозначается . Используя принцип умножения легко показать, что

, где n!=1^.2^. ... ^.n, (0!=1).

Пример 2.4. Сколько трехзначных чисел можно составить из цифр 1; 2; 3; 4; 5 так, чтобы ни одна из цифр не повторялась более одного раза?

Каждое трехзначное число указанного вида является размещением трех цифр из пяти данных в вопросе. Поэтому количество таких чисел равно .

Размещения из n элементов по n называется перестановками множества из n элементов. Число всех различных перестановок множества из n элементов обозначается через . Очевидно,.

Пример 2.5. Сколькими способами можно поставить на полке пять томов “Математической энциклопедии” ?

Каждой расстановке пяти книг на полке соответствует перестановка пяти чисел 1, 2, 3, ..., 5, поэтому существует способов расстановки 5 томов “Математической энциклопедии”.

Любое k-элементное подмножество множества из n элементов называется сочетанием из n элементов по k. В отличие от размещений сочетания являются неупорядоченными подмножествами и поэтому различаются только своими элементами. Число всех различных сочетаний из n элементов по k обозначается через или. Любое размещение изn элементов по k можно получить двумя последовательными действиями : а) - выбор сочетания из n элементов по k; в) - расстановка k элементов выбранного сочетания в определенном порядке. Очевидно, число всех различных размещений из n элементов по k равно ,

В частности, если имеется множество из объектов двух видов (элементов первого вида и — второго), из которых требуется выбрать элементов, среди которых должно бытьпредметов первого типа и второго, то число всех различных выборок такого вида равно: .

Пример 2.6 Сколькими способами можно выбрать из 30 учеников класса 6 дежурных?

При выборе группы дежурных играет роль только состав группы и не играет роли порядок выбора, поэтому 6 дежурных можно выбрать способами .
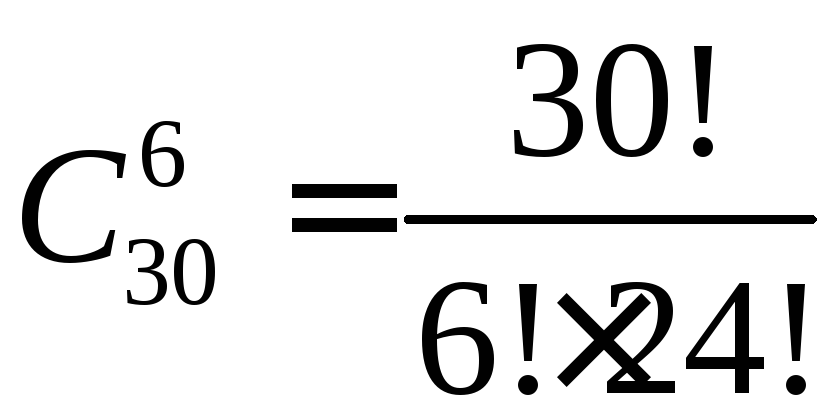