4. Мода и медиана

4.5.1МодараспределенияМо – наиболее часто встречающийся её элемент. В дискретном распределении выборки мода – варианта (варианты), имеющая наибольшую частоту.

Мода распределения может быть единственной и распределение называться унимодальным, либо может быть несколько элементов (вариант) с наибольшими частотами и распределение в этом случаебимодальное(при двух модах) илимногомодальное.

В интервальном унимодальном распределении для нахождения его моды сначала определяется модальный интервал с номером i, имеющий наибольшую частоту . Само значение моды в этом случае находится по формуле :

.

При построенной гистограмме с равными промежутками (плотности распределения) мода может быть найдена графически:

• Правую вершину модального прямоугольника соединяют прямой с правой вершиной предыдущего прямоугольника;

• Левую вершину модального прямоугольника соединяют прямой с левой вершиной следующего прямоугольника;

• Абсцисса точки пересечения построенных прямых является модой.

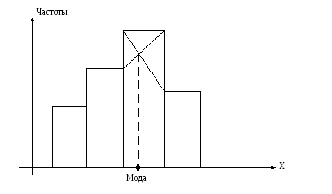
В этом случае может получиться числовое значение, которое в данной выборке не наблюдалось.

4.5.2 Медиана распределенияМе – элемент выборки, сумма частот слева от которой в вариационном ряде равно сумме частот справа.

При дискретном распределении выборки медиана – такая варианта, для которой сумма частот слева и справа не превосходит половины объёма выборки. По накопленным частотам (обычно от наименьшего значения) находят её положение в вариационном ряде, затем указывают значение.

При интервальном распределении выборки медианным является промежуток с номером i, начиная с которого сумма накопленных частот превысит половину объёма выборки (сумма накопленных относительных частот превысит 0,5). Само значение медианы находится по формуле:

.

При известной эмпирической плотности распределения, медиана даёт такое значение у=Ме, при котором соответствующая горизонтальная прямая делитпополамплощадь криволинейной трапеции (ограниченную ось абсцисс и графиком ).

При построенной кумуляте (накопленных частотах или относительных частотах элементов, лежащих левее х ) медиану можно найтиграфически:

• На оси ординат откладывают точку, делящую пополам наибольшую ординату (0,5 или );

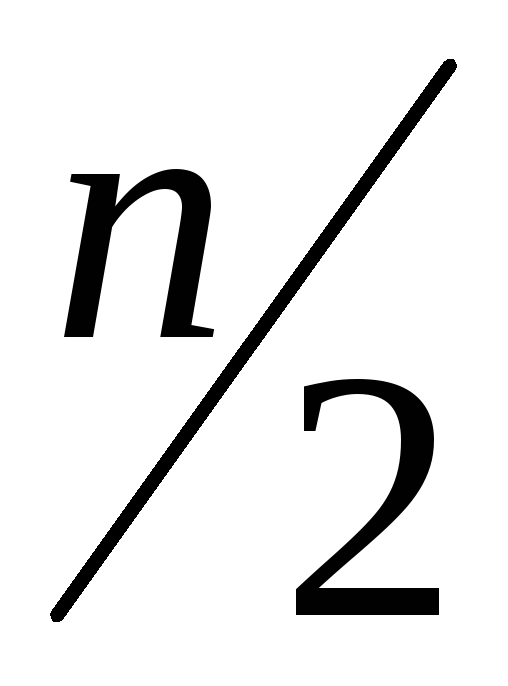• Через отложенную точку проводят прямую, параллельную оси ординат и находят точку её пересечения с кумулятой;

• Абсцисса точки пересечения является медианой.

В этом случае может получиться числовое значение, которое в данной выборке не наблюдалось.

4.2 Виды статистических оценок. Исправление дисперсии

Для различных числовых показателей генеральной совокупности (исследуемой случайной величины Х) по выборке находятся их статистические оценки, которые являются точечными т.к. имеют вид. Важно представлять, можно ли полученной оценкой приближать значение интересуемого числового показателя.

4.2.1Выборочное среднееявляетсяточечной оценкойгенерального среднего(математического ожидания исследуемой случайной величины ).

Такая оценка является

• несмещенной ,т.е. ожидаемое значениене должно

отличаться от искомого значения;

• эффективной, при данном объёме выборкиnдает наименьшую

дисперсию для разных точечных оценок;

• состоятельной, пристремится по вероятности к, т.е.

увеличение объёма выборки даёт всё более точную оценку искомой величины.

Следовательно, математическое ожидание исследуемой случайной величины Х можно приблизить значением выборочного среднего , причем погрешность приближения стремится к нулю при увеличении объёма выборки.

4.2.2Выборочная дисперсия являетсяточечной оценкой генеральной дисперсии(дисперсии исследуемой случайной величины).

Такая оценка является

• эффективной ,

• состоятельной,

• смещенной,, из теории вероятностей получено.

В связи с этим помимо выборочной дисперсии вычисляют также иисправленную дисперсию, обозначаемую. В этом случае исправленное среднее квадратичное является квадратным корнем из исправленной дисперсии,.

Исправление дисперсиипроизводится по правилу.

• Если вычисления выборочной дисперсии производятся по определению, то можно сразу выполнять её исправление: ,

;

• Если вычисление выборочной дисперсии выполняется по свойству, то её исправление выполняется по правилу:

;

• В случае интервального распределения выборки в перечисленные формулы исправления дисперсии и нахождения Sвместоподставляют– середину промежутка (или другой выбранный представитель).

Замечание: При достаточно большом объёме выборки (n50 ) исправление дисперсии можно не производить т.е. взять,.

Пример 5:

Вычислить ,D_в,S, если распределение выборки имеет вид:

x	68	168	268	368
nx	30	20	40	10

.

Решение:

Объем выборки n=30+20+40+10,n=100 .

1 способ:

.

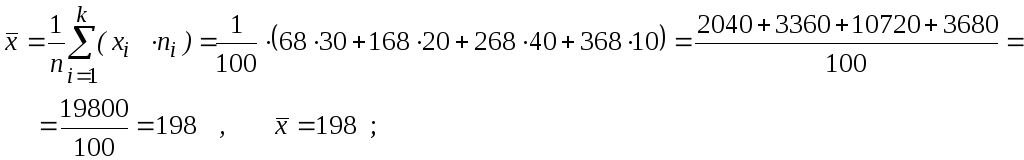
Выборочную дисперсию можно было вычислить, воспользоваться свойством:

=

.

2 способ

Вычисления иD_в можно упростить если заметить, что

т

.е. , ,

где распределение Yимеет вид:

Y	0	1	2	3
ny	30	20	40	10

.

В этом случае (воспользовавшись свойствами),

Исправление дисперсии не производилось, считая n=100 достаточно большим.

Ответ:=198,D_в=10100,S=100,499.