2.3 Эмпирическая плотность распределения

Если при составлении интервального распределения выборки взяты промежутки неравной длины с шагами, то большая высота столбца в гистограмме частот может появиться за счет большей длины данного промежутка и не показывать реальную вероятность нового значения попасть в этот промежуток. Данный недостаток помогает исправить дополнительное построение эмпирической плотности распределения.

Эмпирическая (выборочная) плотность распределения– ступенчатая функцияf^*(x), где высота ступени на промежутке с номеромiберется из условия, что площадь прямоугольника на этом участке равна относительной частотепопадания в такой промежуток. Тем самым и значение эмпирической плотности на данном промежутке вычисляется по правилу, гдеi− номер промежутка.

Добавка «эмпирическая» переводится как «наблюдаемая» и может быть заменена на «выборочная». Значение показывает относительную частоту, приходящуюся на единицу длины промежутка с номеромi. Чем больше высота ступениf^*(x) на промежутке с номеромi, тем больше относительная частота попадания в малый участок этого промежутка.

При сжатии промежутка с сохранением частоты попадания в него, происходит увеличениезначения, при растягивании промежутка значенияуменьшается.

Если выполнено т.е выбран равный шаг разбиения то ступенчатая функцияf^*(x) получается из верхних границ гистограммы частот изменением масштаба по оси ординат делением частотn_i наnh. В этом случае.

Рисунок 3а

…….. ..

Иногда, для удобства изображения вместо ступенчатой функции y=f^*(x) дополнительно строят ломаную, соединяющую соседние точки с координатамии, где— серединаi-го промежутка (или другой его представитель), см. Рис.3б.

Получаем подобие полигона распределения.

4. Эмпирическая функция распределения

и другие кумулятивные кривые

• Из теории вероятностей известно, что функции распределения случайной величины Х имеет вид и она в точкех₀ показывает вероятность для Х принимать значения, меньшие заданногох₀ (вероятность оказаться слева от х₀).

Эмпирическая функция распределения задаётся аналогично функции распределения случайной величины и обозначается. Значение эмпирической функции распределения в точкехравно сумме относительных частотдля всех элементовx_j выборки, меньших взятогох,.

При дискретном распределении выборки функция показывает суммарную относительную частоту элементов выборки, меньших указанного числах. Функцияпринимает значения от 0 (прихменьше минимального элемента выборки), до 1 (прих больше максимального элемента выборки). При дискретном распределении выборки функцияимеет вид:

.

График функции является ступенчатой линией с высотой очередной ступени равной относительной частоте пройденной варианты(слева направо) как на Рисунке 4. Справедливо и обратное: изменение высотыF^*при переходе через точку х(слева направо) равна относительной частоте соответствующей вариантых.

Для интервального распределения выборки изменение высоты F^*при переходе левую границуi-го промежутка равна относительной частотепопаданий в данный промежуток.

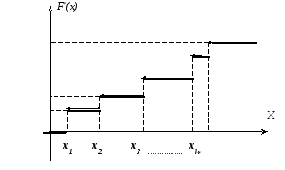
При этом соседние точки ичасто соединяют отрезками прямых, получая ломаную.

• Эмпирическая функция распределения F^* относится к числукумулятивных кривых иликумулят, которые изображают изменение накопленного признака при изменении аргумента. ДляF^*указывается суммарная относительная частота элементов выборки, лежащих левеехпри изменениих. Можно строить также кумулятивные кривыедругих видов:

1. Кривая накопленных частотэлементов выборки, лежащих правеех. Высоты точек при этом будут меняться от 0 в левой части доn справа и полученная функцияF^*(х) является неубывающей;

2. Кривая накопленных частотэлементов выборки, лежащих правеех.Высоты точек при этом будут меняться отn в левой части до 0 справа и полученная функция является невозрастающей;

3. Другие кумулятивные кривые (кумуляты), например огива.

Огивой или эмпирической квантильной кривойявляется кривая, которая указывает изменение значений исследуемого признака Х в зависимости от изменения частоты либо относительной частоты.

Огивы можно получить из соответствующей кумулятивной кривой перестановкой зависимой и независимой переменных. Следовательно, функции, задаваемые парами таких кривых, являются взаимообратными. График огивы по соответствующей кумуляте можно построить, выполняя симметрию исходной кумуляты относительно прямой у=хс учётом масштаба. При небольшом числе искомых точек можно находить зависимость значений для Х по относительной частоте непосредственно по графику эмпирической функции распределения.