3. Теоретическое распределение

8.3.1 По виду распределения выборки предполагается распределение исследуемой случайной величины Х, по выборочным данным находятся точечные оценки параметров распределения;

8.3.2 По предположенному распределению находятся

–значения теоретической функции распределения,

–вероятность значения (или попадания вi-й промежуток)по виду распределения либо,

–значения теоретической плотности распределения Х

на границах и в серединах промежутков (для непрерывной Х),

–выравнивающая частота значения (i-го промежутка);

8.3.3 Проверяется согласованность выборочных и теоретических данных, используя критерий согласия Пирсона (Романовского, Колмогорова и др.).

При предположении нескольких распределений выбирается одно, дающее наилучшее согласование;

8.3.4 Для сравнения выборочных и теоретических данных в одной системе координат строится полигон выборки и полигон теоретического дискретного распределения, гистограмму частот выборки и гистограмму выравнивающих частот, эмпирической и теоретической плотности распределения либо эмпирической и теоретической функций распределения;

8.3.4 При взятом уровне достоверности и уровне значимости получают интервальные оценки параметров распределения;

8.3.5 По виду распределения прогнозируется вероятность получить случайное значение Х=алибо.

9 Пример обработки статистических данных

В результате 30 измерений случайной величины Х при одинаковых условиях получены данные, записанные в таблице

.

По выборочным данным требуется:

1. Разбить элементы выборки на 7 равных промежутков, составить статистический ряд распределения;

2) Построить гистограмму частот, графики выборочной плотности и выборочной функции распределения;

3) Найти выборочное среднее , выборочную дисперсию и выборочное исправленное среднее квадратичное отклонениеS ;

4) Записать теоретическую плотность распределения f(x), предполагая нормальное распределение Х, построить её график вместе с графиком эмпирической плотности распределения .

Оценить согласованность нормального распределения с выборочными данными, используя критерий Пирсона или Романовского.

В случае согласованности выборочных данных с нормальным распределением найти доверительные интервалы для М(Х) и Х

5) Предполагая равномерное распределение Х найти его параметры и записать плотность распределения f(x), оценить его согласованность с выборочными данными;

6) Среди рассмотренных распределений (нормального и равномерного)

выбрать лучшее согласование с выборкой,

с его помощью найти вероятность попадания Хв промежуток (10;20).

Решение:

1) Составим распределение выборки.

В результате ранжирования по возрастанию элементов выборки получается вариационный ряд:

–1; 2; 6; 6; 10; 10; 11; 11; 15; 15; 15; 18; 18; 18; 18;

20; 20; 20; 20; 24; 24; 24; 28; 28; 30; 30; 34; 34; 41; 41. Объем выборки n=30 (количество элементов).

Среди элементов выборки имеются повторяющиеся, составим статистический ряд:

Варианты х	-1	2	6	10	11	15	18	20	24	28	30	34	41
Частоты nх	1	1	2	2	2	3	4	4	3	2	2	2	2

х_min= –1,x _max=41, размах выборки.

Число интервалов k=7 (по условию), найдем шагразбиения.

Распределив 30 элементов выборки на 7 равных промежутков, получим сгруппированный (интервальный) статистический ряд:

Номер i	1	2	3	4	5	6	7
Границы промежутка	(-1; 5)	(5;11)	(11;17)	(17;23)	(23;29)	(29;35)	(35;41)
Середина xio	2	8	14	20	26	32	38
Частота ni	2	5	4	8	5	4	2

Варианта х=11 попала на границу второго и третьего промежутков, её частота (2) распределилась поровну между этими промежутками, хотя можно было учитывать её частоту только в левом (втором) промежутке.

Можно получить другой статистический ряд, если крайние значения принять за середины крайних промежутков, при этом шаг разбиения , размах выборки увеличится, статистический ряд примет вид:

Номер i	1	2	3	4	5	6	7
Границы промежутка	–4,5 2,5	2,5 9,5	9,5 16,5	16,5 23,5	23,5 30,5	30,5 37,5	37,5 44,5
Середина xio	-1	6	13	20	27	34	41
Частота ni	2	2	7	8	7	2	2

Система MathCAD2001 при составлении статистического ряда с семью равными промежутками к максимальному значениюх=41 прибавила 1 и нашла шаг разбиения. В результате получилось распределение

Номер i	1	2	3	4	5	6	7
Границы промежутка	-1 5,14	5.14 11.28	11.28 17.42	17.42 23.57	23.57 29.71	29.71 35.85	35.85 42
Середина xio	2,071	8,214	14,357	20,5	26,643	32,786	38,929
Частота ni	2	6	3	8	5	4	2

Как видно из этих трёх статистических рядов, важно договориться о способе разбиения данных и составления интервального ряда.

Дальнейшие преобразования будем выполнять с первым из полученных статистических рядов ().

Все результаты будем записывать в сводные таблицы 4 и 5.

2. Гистограмма частот и график

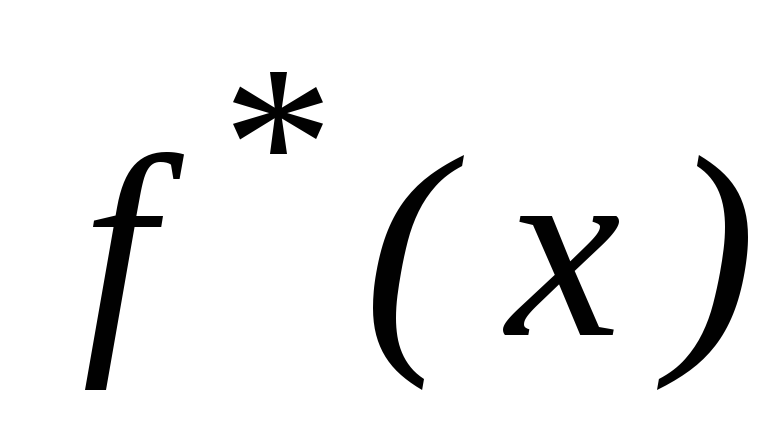
Гистограмма частот

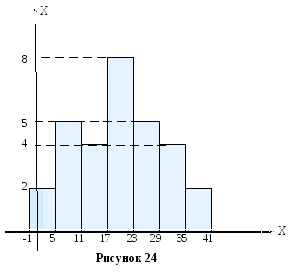
Вычислим значения эмпирической плотностина каждом промежутке, т.к. шаг равный:

Эмпирическая плотность распределения

3) Числовые характеристики выборки ( ,D_в, S ):

1 способ:

Исправленная дисперсия (т.к n<50);

Исправленное среднее квадратичное отклонение .

2 способ:

При вычислении можно было воспользоваться тем, чтогде статистическое распределениеYимеет вид

Y	0	1	2	3	4	5	6
ny	2	5	4	8	5	4	2

тогда

исправленная дисперсия ;

3 способ:

Можно ввести «ложный ноль», например с=20 и вспомогательную

величину Х–с, имеющую распределение

x-c	-18	-12	-6	0	6	12	18
ni	2	5	4	8	5	4	2

,

тогда

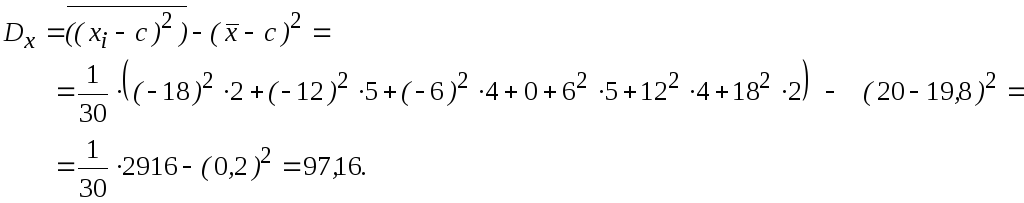Исправленная дисперсия ,

В результате получили ;

4 Предположим нормальное распределение для Х.

В общем случае плотность нормального распределения .

Параметры нормального распределения аинайдём из точечных оценок:, тогда

.

Для каждого промежутка с номером i( 1i7) (см. сводную таблицу 4)

–нормированная нормальная случайная величина;

–функция распределения на границах, значения Ф(х)

находятся по таблице (приложение 2).

Например при ,

при и т.д.;

–вероятность попадания в промежуток (двумя способами

и ), на крайних промежуткахP₁+P₂и

P₆+P₇ (уменьшив число промежутков);

–выравнивающие частоты ( округляя), их сумма должна быть равна

исходному объёму выборки (оказалась меньше из-за округления);

–выборочное значение Хи-квадрат (сумма по

последней строке), число промежутков k=7–2 уменьшено из-за

объединения крайних промежутков (т.к. частоты n₁=2,n₇=2 малы).

При гипотезе о нормальном распределении получили .

По таблице (приложение 5) при числе степеней свободыr= 5–3=2 и уровне значимости=0,05 найдемПолучили, гипотеза о нормальном распределениине отвергается.

Сводная таблица 4

№	i	1	2	3	4	5	6	7
1	(xi; xi+1)	-1–5	5–11	11–17	17–23	23–29	29–35	35-41	–
2	xi0	2	8	14	20	26	32	38	–
3	ni	2	5	4	8	5	4	2	30
4		0,0667	0,1667	0,1333	0,2667	0,1667	0,1333	0,0667	1,000
5		0,0111	0,0278	0,0222	0,0444	0,0278	0,0222	0,0111	–
6		0,0667	0,2333	0,3667	0,6333	0,8000	0,9333	1,0000	–
7		-1,776	-1,177	-0,579	0,02	0,618	1,217	1,815	–
8		0,0825	0,2000	0,3380	0,3989	0,3300	0,1900	0,0770	–
9		0,0082	0,0200	0,0337	0,0398	0,0329	0,0190	0,0077	–
10		0,019 0,070	0,070 0,190	0,190 0,390	0,390 0,625	0,625 0,820	0,820 0,935	0,935 0,983	–
11		0,051	0,120	0,200	0,235	0,195	0,115	0,048	0,964
12		0,049	0,120	0,202	0,239	0,1974	0,1140	0,0462	0,964
13		1,53	3,60	6,00	7,06	5,86	3,44	1,43	29
		5,13					4,87
14		–1,87		-2,00	0,94	–0,86	1,13		–
15		3.947		4,0000	0,8836	0,7396	1,2769		–
16		0,682		0,667	0,125	0,126	0,262		1,862

Доверительные интервалыпараметров нормального распределения при уровне достоверности=95%:

а) Доверительный интервал для математического ожиданиянайдём по правилу, т.к. объём выборкиn=30 можно считать малым (n<50). Значениенайдём из таблицы (приложение 3) приn=30 и, получим.

Подставив n=30,S=10,025 ,=19,8 получим радиус интервала,.

С вероятность не менее =95%;

б)Доверительный интервал для среднего квадратичного отклонения

найдём по правилу

Значение найдём по таблице (приложение 4) приn=30 и, получив.

В таком случае ,.

С вероятность не менее =95%.

Числовые характеристики иSдля репрезентативных выборок (достаточно большого объёма), элементы которых – значения той же случайной величиныХ, будут принимать случайные и каждый раз различные значения.

Найденные доверительные интервалы говорят о том, что с вероятностью 95% (допуская в среднем 5 ошибок из ста случаев) можно предполагать:

• выборочное среднее примет значение от 16 до 23,5;

• исправленное выборочное среднее квадратичное отклонение Sпримет значение от 7,2 до 12,8 .

Обработка данных, полученных при других способах составления статистического ряда в п.1, дает иные значения выборочного среднего и среднего квадратичного. Каждый из результатов незначительно отличается от найденного данным способом и принадлежит доверительному интервалу.

5 Предположим равномерное распределение.

Плотность равномерного распределения .

Параметры аиbнайдутся из условия,S=10,025 ,=19,8.

В результате вычислений получим а=2,436,b=37,163.

На отрезке [a;b] плотность равномерного распределенияи за пределами отрезка [a;b] равна нулю.

Согласованность выборочных данных с равномерным распределением проверим с помощью критерия Пирсона (Хи-квадрат). Все вычисления указаны в сводной таблице 5.

Сводная таблица 5

№	i	1		2	3	4	5	6	7
1	ni	2		5	4	8	5	4	2		30
2	(xi; xi+1)	-1– a	a– 5	5–11	11–17	17–23	23–29	29–35	35 – b	b– 41	–
3		0	0,074	0,173	0,173	0,173	0,173	0,173	0,062	0	1
		0,247						0,235
4		7,41			5,19	5,19	5,19	7,05
5		–0,41			–1,19	2,81	–0,19	–1,05			–
6		0,168			1,416	7,896	0,036	1,103			–
7		0,023			0,273	1,521	0,007	0,156			1,980

–вероятность попадания в каждый промежуток

Если бы исследуемая случайная величина Химела равномерное распределение, то её значения лежали бы в отрезке, вероятности попадания в отрезки [-1;a] и [b; 41] были бы равны нулю. Поэтому первый и последний промежутки разбиты в сводной таблице 5 на две части.

В случае, когда хотя бы одна из границ отрезка [a;b] выходят за внешние границы (aменьшеилиbбольше), то рассматривается дополнительный промежуток с нулевой частотой и ненулевой выравнивающей частотой;

–выравнивающая частота каждого промежутка.

В результате вычислений .

По таблице ,т.е. гипотеза о равномерном распределениине отвергается.

6 Прогнозирование

Среди рассмотренных распределений лучшее согласование с выборочными данными дает нормальное распределение, т.к. при сравнении выборочных значений Хи–квадрат 1,862 < 1,980. Для данного статистического распределения выборки различие найденныхдля разного вида распределений достаточно мало, что говорит о почти равной возможности как нормального, так и равномерного распределения исследуемого признака Х.

Построим в одной системе координат гистограмму эмпирических частот, выравнивающих частот по нормальному распределению и выравнивающих частот по равномерному распределению (Рис. 26). Одновременно изобразим нормальную кривую, взяв в каждой её точке высоту у= .

Вероятность попадания Х в промежуток (10;20) :

а) При нормальном распределении

б) При равномерном распределении