5.2 Непрерывные случайные величины

Непрерывная случайная величина Х описываетсяс помощью

1. Плотности распределения f(x).

Для f(x)выполнено:

• График у= f(x)лежит выше оси абсцисс, f(x);

• Если , то при;

• Площадь, ограниченная графиком у= f(x)и осью Ох, равна 1;

2. Функции распределения F(x).

Для F(x) выполнено:

• ;

• ;

• ;

3. Числовых характеристик

• , ;

• , ;

• .

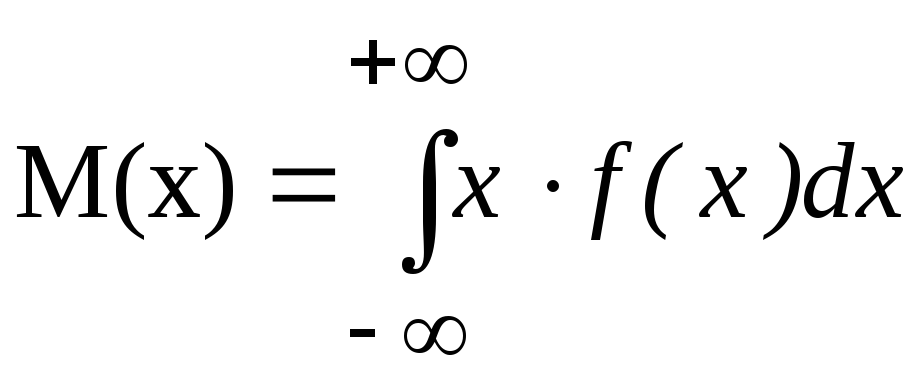Перечислим основные виды распределенийнепрерывных случайных величин и укажем правила нахождения их параметров по статистическим данным.

1. Равномерноераспределение

Пусть случайная величина Х принимает значения из отрезка [a;b], вероятность попадания в малый участок этого отрезка не зависит от его положения в отрезке [a;b] и зависит только соотношения длин этих отрезков.

Вэтом случае Х имеетравномерное распределение,

плотность равномерного распределения .

Чем больше длина отрезка [a;b] (разница междуa и b ), тем меньше значение функцииf(x)=на этом отрезке (см. Рис.17). .

График плотности равномерного распределения имеет следующий вид :

В случае равномерного распределения

• Функция распределения

• Вероятность попадания значений случайной величины Х в отрезок [x₁;x₂] длиныL(полностью лежащий в отрезке [a;b] )находится как отношение его длины к длине отрезка [a;b];

• Математическое ожидание (середина отрезка);

• Дисперсия ;

• .

Замечание: Равномерное распределение предполагается при малом отличии полигона или графикаотрезка от горизонтальной прямой, за пределами которого нулевые значения.

Параметры a и bравномерного распределения по статистическим данным находятся из оценок:

, , т.е. . ;

2. Показательное распределение

Случайная величина Х имеет показательное распределение, если

плотность её распределения имеет вид .

.

График плотности показательного распределения

Функция распределения для показательного распределения называется функцией надёжности.

Вероятность попадания в промежуток .

Для показательного распределения .

Замечание: Показательное распределение предполагают, когда гистограмма или график эмпирической плотности до нулевого значения практически нулевые и значенияиS мало отличаются.

Для случайной величины Х, имеющей показательное распределение, параметром служит , её значение по выборочным данным может быть найдено следующим образом:

1) Для выборки х₁,х₂, …..,х_nнаходим.

Если иS существенно отличаются, то показательное распределение вряд ли имеет место;

2) Из оценки и условия, получаем ;

В общем случае показательное распределение может иметь два параметра, плотность распределения при этом 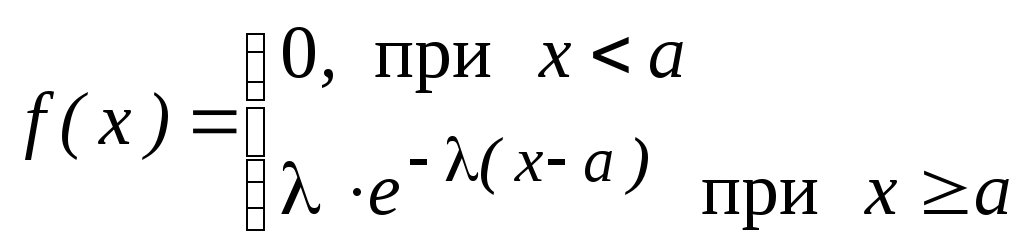(см. Рис.18.б).

Число показывает пологость кривой и наибольшую высоту, числоа показывает сдвиг относительно осиОу.

В этом случае числовые характеристики .

Замечание: Такое распределение предполагается, когда гистограмма или графикдо значениях = амало отличаются от нуля, а послех = аявляется убывающей и стремящейся к нулю. Значения–аидолжны мало отличаться.

В этом случае (при известном числе а) параметрнаходится из оценкит.е., ;

3. Нормальноераспределение

Нормальное распределениеимеет плотность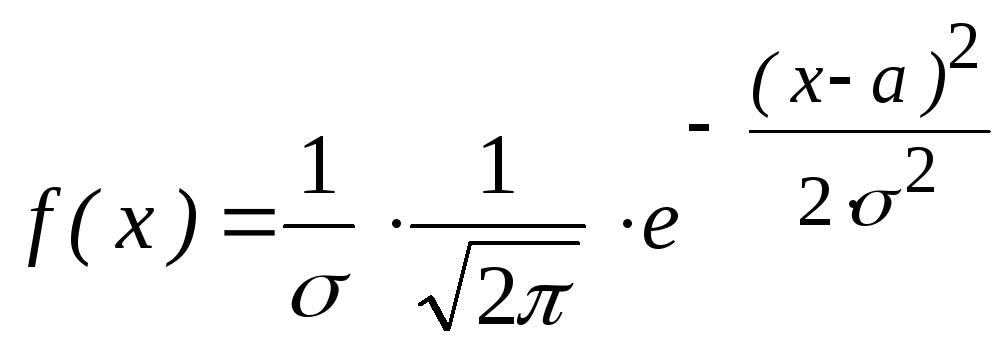, график которой является колоколообразным (с одной точкой максимума).

На Рис.19 показаны графики плотностей нормального распределения с параметрами а₁=20 и₁=15 ,а ₂=20 и₂=8,а₃=35 и₃=5.

Для нормального распределения параметр а показывает абсциссу точки максимума, параметрпоказывает отклонение отх=а(влево и вправо) абсцисс точек перегиба. Чем меньше значение, тем плотность распределения имеет более крутой график с большим значением функции в точке максимума.

Для нормальной случайной величины Х, имеющей параметры а =0 и =1 (нормированной) плотность распределения обычно обозначается ,. Графиксимметричен относительнох=0 (осиОу) и точки её перегиба при.Функцияявляетсячётной ,.

Значения призаданы в таблице (приложение 1),

при считаем=0.

Функция распределения F(x) приа=0 и=1 имеет видF(x)=0,5 + Ф(х), где–нечётнаяфункция т.е. Ф(-х)= –Ф(х).

Значения Ф(х) заданы в таблице (приложение 2),при х>5 считаемФ(х)=0,5.

Значения плотности произвольного нормального распределения можно найти, используянормированнуюслучайную величину, тогда. Графикf(x) получается из графикасжатием враз вдоль осиОх(растяжением враз вдоль осиОхпри<1) и переносом наaвправо (приа<0 сдвиг влево).

Д

F(x)=0,5 +Ф

ля произвольной нормально распределённой случайной величины Х функция распределения,

используя функцию Ф(х) получим соотношение .

Вероятность нормальной величиной принимать значения от х₁дох₂находится по правилу.

Из этого

а)—вероятность

значений нормальной случайной величины, не превосходящих х=х_{0 ;}

б)—вероятность

значений нормальной случайной величины, превосходящих х=х_{0 .}

Вероятность отклонения нормальной величины от своего математического ожидания на величину, не превышающую , находится по правилу. Если взять, то,, (Ф(3)=0,49865 из таблицы).

«Правило трёх сигма»:

«вероятность отклонения нормальной случайной величины от своего математического ожидания на величину, большую трёх среднеквадратичных отклонений, составляет не более 0,3% ».

Следует обратить внимание, что нормальное распределение аппроксимирует (приближает) как биномиальное распределение, так и распределение Пуассона при увеличении числа испытанийm. При этом получим параметры нормального распределенияпри биномиальном распределении,для распределения Пуассона.

Если Х₁, Х₂, … , Х_n— нормальные случайные величины с известными математическими ожиданиямии среднеквадратичными отклонениями, то их взвешенная суммаявляется такженормальной величинойс параметрамии.

Центральная предельная теорема:

ЕслиХ₁, Х₂, …. , Хn– независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием М(X) и дисперсиейD(X),тозакон распределения их суммыпри неограниченном увеличении числа слагаемыхnприближается к нормальному распределению с математическим ожиданиеми дисперсией.

Замечание: Обычно распределение суммы независимых случайных величин считают нормальным приn>8. Такая сумма может считаться случайной величиной со свойстваминормальнойслучайной величины.

Посчитаем элементы выборки х₁,х₂, …..,х_nзначениями случайных величинс одинаковым распределением (с одинаковыми математическими ожиданиямиМ(Х) и дисперсиямиD(X)при репрезентативности выборки).

В этом случае их сумма (при объёме выборки n>8) распределена нормально, как и случайная величина. Её математическое ожидание является суммой математических ожиданийи её дисперсия находится по правилу,.

Учитывая, что , получим:

1) (несмещённость оценкиМ(Х) с помощью);

2) т.е. выборочное среднее — случайная величина ,

разброс значений для которой убывает и стремится к нулю при увеличении

объёма выборки.

Замечание :Нормальное распределение предполагают, когда гистограмма или графикимеют близкую к колоколообразной форму.

Для случайной величины Х, имеющей нормальное распределение, параметрами служат аи, их значения по выборочным данным могут быть найдены следующим образом:

1. По выборочным данным находятся ;

2. П

   

   араметрынаходятся из оценок,

т.е. ;