Лекции по ТПР / Функциии полезности

ФУНКЦИИ ПОЛЕЗНОСТИ

В данном разделе рассмотрены три функции полезности, основанные на понятиях независимости по предпочтению и независимости по полезности критериев. Прежде чем переходить к рассмотрению конкретных функций, введём некоторые обозначения.

Для каждого критерия kj (j=1,…,т) определим области определения: k – наименее j

ние. В зависимости от содержания критерия в качестве k j может быть минимально

допустимое значение (примером такого критерия является тактовая частота процессора ПЭВМ) или максимальное из допустимых (стоимость ПЭВМ). Также и k j может

чений следующие записи функции полезности идентичны:

В последующих пунктах данного раздела будут рассмотрены полилинейная, мультипликативная и аддитивная функции полезности. Для каждой функции будут сформулированы условия её существования, т.е. условия, когда она может обоснованно использоваться, а также изложены вопросы определения её параметров.

ПОЛИЛИНЕЙНАЯ ФУНКЦИЯ ПОЛЕЗНОСТИ

Прежде чем переходить к рассмотрению условий существования полилинейной функции, введём определение независимости критерия от своего дополнения.

Определение 3.1. Критерий kj независим по полезности от своего дополнения k j , если функция полезности представляется в виде

Поясним содержательный смысл (3.1). Для этого построим функцию полезности в зависимости от одного критерия kj (рис.3.1). Это не что иное, как условная функция

Перейдём к другой условной функции полезности, поменяв значения критериев,

Условие (3.1) означает, что две любые условные функции полезности связаны между собой положительным линейным преобразованием. Действительно,

Поменяв значения критериев, входящих в дополнение на k 2j , вновь построим нормированную условную функцию. Если эта функция не изменяется при изменении до-

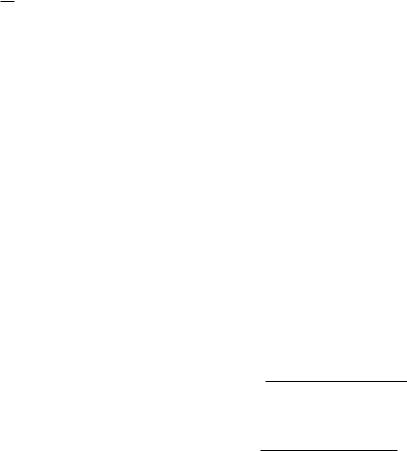
полнения, то, значит, выполняется условие независимости по полезности критерия от своего дополнения. Тогда нормированная условная функция полезности не зависит

Рассмотрим сначала полилинейную функцию полезности для случая двух критериев k1 и k2.

Теорема 3.1. Если k1 независим по полезности от k2, а k2 – от k1, то функция полезности имеет вид

U( k1,k2 ) = W1U1( k1 ) + W2U2( k2 ) + (1 - W1 - W2 )U1( k1 )U2( k2 ),

(3.2)

где U1(k1), U2(k2) – нормированные условные функции полезности; W1, W2 – шкалирующие коэффициенты.

Доказательство. Из условия независимости по полезности k1 от k2 следует:

Введём в рассмотрение шкалирующие коэффициенты:

Подставляя последнее выражение в (3.8), после упрощения получим искомое (3.2).

Параметры полилинейной функции полезности. Чтобы использовать функцию (3.2)

на практике, необходимо:

а) построить нормированные условные функции полезности U1(k1), U2(k2) и убедиться, что они независимы;

б) задать шкалирующие коэффициенты W1 и W2, для этого ЛПР необходимо оценить «псевдообъекты», представленные в табл.3.1.

Лицо, принимающее решение, сравнивая с объектами В+ и В-, имеющими соответственно оценки 1.0 и 0.0, должно дать оценки псевдообъектов, которые и являются коэффициентами W1, W2.

Таблица 3.1

Определение шкалирующих коэффициентов

Сформулируем теорему о существовании полилинейной функции полезности для трёх критериев: k1, k2 и k3.

Теорема 3.2. Пусть каждый из трёх критериев независим по полезности от своего дополнения, тогда функция полезности имеет вид

Доказательство данной теоремы приведено в соответствующей литературе. Отметим, что для определения всех коэффициентов Wj для случая трёх критериев ЛПР должно давать оценку уже шести псевдообъектов.

Теорему 3.2 можно обобщить на случай т>3 критериев.

Теорема 3.3. Пусть каждый из критериев kj (j=1,…, т) независим по полезности от своего дополнения, тогда функция полезности имеет вид

где Uj(kj) – нормированные условные функции полезности,

Из вида полилинейной функции следует, что при большом числе критериев она имеет значительное количество коэффициентов, для определения которых требуется от ЛПР много оценок псевдообъектов. Поэтому при т>4 ее использование затруднительно.

МУЛЬТИПЛИКАТИВНАЯ ФУНКЦИЯ ПОЛЕЗНОСТИ

Для формулирования условий существования мультипликативной функции потре-

если порядок многокритериальных объектов в последовательности, образованной из-

дящих в дополнение.

Сравнивая понятие независимости по полезности и по предпочтению, можно сделать вывод, что из независимости по полезности следует независимость по предпочтению.

Определение 3.3. Пара критериев kj и ki независима по предпочтению от своего до-

Для проверки независимости по предпочтению kj и ki от k j ,i необходимо сформиро-

вать множество эффективных объектов (оптимальных по Парето) путём изменения только kj и ki, как показано в табл. 3.2.

Таблица 3.2.

Проверка независимости по предпочтению пары критериев от своего дополнения

Лицо, принимающее решение, должно упорядочить данное множество объектов по предпочтению, например, B6 B7 B5 B8 … B0 Bn.

Далее следует у всех объектов изменить дополнение на k 2j ,i , оставив неизменными

kj и ki, и вновь предложить ЛПР упорядочить объекты. Если порядок объектов остался прежним, то это говорит о том, что есть основание считать, что пара критериев не зависит по предпочтению от своего дополнения. Для большей достоверности следует еще несколько раз изменить дополнение, каждый раз проверяя неизменность порядка

по полезности от своего дополнения, т.е. функцию полезности можно представить в виде

Доказательство данной теоремы приведено в соответствующей литературе. Теорема 3.4 связывает свойства независимости критериев по полезности и по пред-

почтению, что весьма важно, так как проверка независимости по предпочтению пары критериев существенно проще, чем проверка независимости по полезности.

Практическая проверка на независимость по полезности целой группы критериев от дополнения представляет большие трудности. Однако эту задачу можно разбить на

ряд более простых: проверку независимости только отдельных пар критериев. Для этого необходимо воспользоваться следующей теоремой.

Доказательство этой теоремы приведено в соответствующей литературе. Утверждение теоремы 3.5 можно распространить па случай четырёх, пяти и более

критериев. Из неё же следует, что если есть несколько пересекающихся групп критериев, каждая из которых независима по полезности от своего дополнения, то объединение этих групп тоже будет независимо по полезности от своего дополнения. Например, если группы критериев k1, k2, k3 и k1, k6, k8 независимы от своего дополнения, то объединение этих групп (k1, k2, k3, k6, k8) тоже будет независимо от своего дополнения, так как в обеих группах имеется один общий критерий k1.

Определение 3.4. Критерии kj (j=1,…,m) взаимонезависимы по полезности, если любое подмножество критериев независимо по полезности от своего дополнения.

На основе теорем 3.4, 3.5 можно сформулировать следующую теорему.

Теорема 3.6. Если существует один критерий kj, независимый по полезности от своего дополнения, и все пары критериев kj и ki (i=1,…,m; i≠j) независимы по предпочтению от k j ,i , то критерии kj (j=1,…,m) взаимонезависимы по полезности.

Доказательство теоремы следует из предыдущих теорем. Теперь можно перейти к формулированию теоремы о существовании мультипликативной функции.

Теорема 3.7. Если критерии kj (j=1,…,m) взаимонезависимы по полезности, то функция полезности имеет вид

где Uj(kj) – нормированные условные функции полезности; Wj – шкалирующие коэффициенты; С – масштабный коэффициент.

Доказательство. Так как критерии взаимонезависимы по полезности, то подмножество ki также независимо по полезности от ki, т.е.

Тождества типа (3.14) могут быть составлены для любого i=2,…,m. Из них получим

условная функция полезности, а выражение (3.15) принимает вид

Домножив обе части на C и прибавив к ним по единице, а также учитывая (3.16), получим утверждение теоремы (3.11). Так как проверять условия взаимонезависимости критериев по полезности теоремы (3.7) сложно, то условия существования мультипликативной функции можно сформулировать, основываясь на теореме (3.6) в виде следующего утверждения: если существует критерий kj, независимый по полезности от своего дополнения, и все пары критериев kj, ki (i=1,…,m; m≥3; i≠j) независимы по предпочтению, то имеет место мультипликативная функция полезности.

Параметры мультипликативной функции полезности:

Данное уравнение m-й степени имеет корень C=0 и ещё m-1 корней. В функции (3.11) может быть использован масштабный коэффициент, больший минус единицы. Покажем это. Используя (3.12), вычислим значение функции полезности при

k k ( j 1, ,m) : j j

так как Wi≤1, a U (ki , ki ) 0, то из (3.18) следует 1+CWi>0. Подставляя последнее в

(3.17), получим C>-1.

Покажем, что уравнение (3.17) при C>-1 имеет единственное решение, кроме C=0. Уравнение (3.17) идентично следующему равенству:

Функция F(C) имеет первую производную

j 1

Рис.3.3. Функция для определения коэффициента C

следний случай особый, он будет рассмотрен позднее.

Рассмотрим частные случаи мультипликативной функции. Для случая двух критериев функция (3.11) принимает вид

1 + CU(k1,k2) = ( 1 + CW1U1(k1) )( 1 + CW2U2(k2) ). (3.19)

Масштабный коэффициент C определяется из уравнения

1 + C = ( l + CW1 )( l + CW2 ).

Откуда получаем C = ( l - W1 - W2 ) / ( W1W2 ).

Подставляя выражение для C в (3.19), после упрощения получим

U(k1,k2) = W1U1(k1) + W2U2(k2) + ( 1 – W1 - W2 )U1(k1)U2(k2).

Данная функция совпадает с полилинейной функцией (3.2). Этого следовало ожидать, так как условия теоремы 3.1 совпадают с условиями теоремы 3.7 для случая двух критериев.

Случай трех критериев. Мультипликативная функция имеет вид

Масштабный коэффициент определяется из уравнения

1 + C = ( l + CW1 )( l + CW2 )( l + CW3 ).

Раскрыв правую часть и приведя подобные, получим квадратное уравнение

C2W1W2W3 + C( W1W2 + W1W3 + W2W3 ) + W1 + W2 + W3 – 1 = 0.

Один из квадратных корней квадратного уравнения будет больше -1, он является искомым и используется в (3.20).

Следует отметить, что мультипликативная функция является частным случаем полилинейной функции, так как условия теоремы 3.3 выполняются и для мультипликативной функции.

АДДИТИВНАЯ ФУНКЦИЯ ПОЛЕЗНОСТИ

Это наиболее простая и часто употребляемая функция полезности имеет вид

где Uj(kj) – нормированные условные функции полезности; Wj – шкалирующие коэффициенты.

Чтобы аддитивная функция изменялась в интервале [0;1], на Wj накладывается ограничение.

Рассмотрим условия её существования в развитии мультипликативной функции полезности. Дело в том, что аддитивная функция является частным случаем мультипликативной функции.

Теорема 3.8. Пусть выполняются условия существования мультипликативной функции полезности и сумма шкалирующих коэффициентов равна единице, тогда имеет место аддитивная функция полезности.

Доказательство. По условию теоремы

m

W j 1,

j 1

тогда масштабный коэффициент C мультипликативной функции равен пулю. Проана-

лизируем, к какому виду преобразуется мультипликативная функция при стремлении C к нулю. С целью более простого доказательства рассмотрим случай трех критериев, при этом общность (число критериев произвольное) не теряется. Перепишем мультипликативную функцию для трех критериев:

1 + CU(k1,k2,k3) = ( 1 + CW1U1(k1) )( 1 + CW2U2(k2) )( 1 + CW3U3(k3) ).

Упростив данное выражение, получим