
Лекции по ТПР / Многокритериальные задачи
.pdfОглавление |
|
МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ .......................................................... |
2 |
Классификация многокритериальных задач ............................................... |
4 |
Проблемы решения МКЗ ............................................................................... |
6 |
Классификация методов решения МКЗ ....................................................... |
8 |
МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Прежде чем переходить к рассмотрению многокритериальных задач, остановимся на предпосылках их постановки, т.е. укажем причины, порождающие проблему многокритериальности. Для этого обратимся к блок-схеме, приведенной на рис.1.1. Данная схема отражает рациональную логическую последовательность этапов при подготовке и принятии решений.
С проблемой многокритериальности лицо, принимающее решение (ЛПР), сталкивается на этапе 7. Вместе с тем, ЛПР на более ранних этапах (2 и 3) сам предопределяет постановку многокритериальной задачи. Следовательно, предпосылкой постановки многокритериальной задачи является необходимость проведения этапа 3 (формирования системы критериев). Этот этап может и отсутствовать, если цель принятия решения четко определяется одним критерием.
В практических задачах цель – весьма сложное понятие, которое даже содержательно не всегда удастся четко определить, тем более, количественно измерить степень ее достижения. Поэтому осуществляется декомпозиция сложного понятия "цель принятия решения" на более простые единичные критерии, каждый из которых может быть количественно измерен. В большинстве случаев в качестве единичных критериев используются общепринятые характеристики исследуемого объекта, измеряемые по шкалам интервалов или отношений.
Полное и четкое описание цели множеством критериев является основой успешного решения поставленной задачи принятия решений.
Таким образом, причинами проведения этапа 3 и, соответственно, предпосылками постановки многокритериальных задач являются сложность цели принятия решений и трудность измерения степени достижения цели различными вариантами решения задачи.
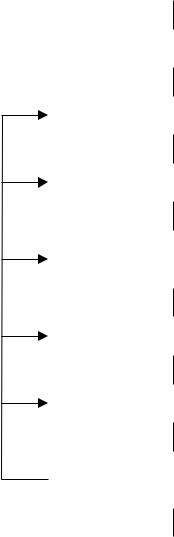
1.Постановка и анализ задачи (проблемной ситуации)
2.Формулирование цели принятия
решения
3. Формирование системы критериев оценки вариантов решения задачи
4. Генерирование вариантов решения задачи
5. Разработка или выбор методов и моделей оценки вариантов решения задачи по отдельным критериям
6. Оценка вариантов по отдельным критериям
7. Выбор наиболее предпочтительного варианта решения
8. Анализ выбранного варианта решения лицом, принимающим решение
9. Реализация выбранного решения
Рис.1.1. Этапы подготовки и принятия решений
Следовательно, постановку многокритериальной задачи предопределяет сам исследователь (ЛПР) из-за того, что не смог сформировать в математическом виде целевую функцию, а на этапе 7 он сталкивается с необходимостью решения многокритериальной задачи.
Следует отметить, что поскольку описание цели системой критериев является неформальной процедурой, то и последующее агрегирование критериев на этапе 7 также не является формальной процедурой. Поэтому решение многокритериальной задачи не является строгой математической задачей, а представляет собой набор процедур, помогающих ЛПР разобраться и уточнить цель принятия решений, устранить ошибки в своих оценках, сделать свое поведение в процессе выбора рациональным.
Примеры постановок многокритериальных задач из разных областей деятельности:
Выбор площадок для строительства промышленных объектов. В данной задаче необходимо учитывать группы критериев: экономические, экологические, социальные, критерии безопасности и т.д.
Оценка качества продукции (технического уровня разработок) по множеству потребительских свойств. Следствием данной задачи является определение

цены на продукцию на основе потребительских свойств.
Проектирование на основе принципа многовариантности. Каждый из вариантов в абсолютном большинстве оценивается множеством критериев. В этой связи следует подчеркнуть, что системы автоматизированного проектирова-
ния должны включать подсистему выбора и оценки решений по многим критериям.
КЛАССИФИКАЦИЯ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ
Первым признаком, по которому проведем классификацию многокритериальных задач, является характер решаемой МКЗ.
Будем называть дискретными многокритериальными задачами (ДМКЗ) задачи, в которых множество объектов конечно. В задачах этого класса множество многокритериальных объектов в пространстве критериев K1 K2 ... Km представляет собой множество дискретных точек. Дискретные МКЗ чаще всего ставятся в экономике и квалиметрии.
Исходными данными для дискретных МКЗ является матрица значений единичных
критериев |
k j |
, размерности n m, строками которой являются объекты (варианты) |
B |
|
i |
|
i |
|
|
|
(i=l,...,n), а столбцами – критерии kj (j=l,...,m).
Второй класс образует непрерывные многокритериальные задачи (НМКЗ), которые формулируются следующим образом:
Имеется объект исследования, характеризующийся параметрами x1,...,xn. Требуется определить оптимальные в некотором смысле значения этих параметров с учетом нескольких критериев (целевых функций) k1,...,km. При этом задана область определения параметров x1,...,xn и целевые функции k1=f1(x1,...,xn);...; km=fm(x1,...,xn).
Область определения параметров (переменных) A задается обычно в виде системы ограничений, например, в многокритериальных задачах линейного программирования
– система линейных неравенств.
Таким образом, каждый элемент области А характеризуется вектором X {x1 ,..., xn }. Учитывая, что заданы целевые функции, от пространства параметров X1 X 2 ... X n ,
можно перейти к пространству критериев K1 K2 ... Km, и тогда каждый элемент области А будет определяться вектором критериев. Поэтому непрерывную многокритериальную задачу можно рассматривать как задачу, в которой бесконечное множество объектов. Это множество задано в виде области определения в пространстве критери-
ев А(k1,…,km).
Так как непрерывные МКЗ, как правило, возникают при оптимизации параметров сложных объектов, то в литературе их еще называют задачами векторной оптимизации. Одной из задач векторной оптимизации является многокритериальная задача линейного программирования.
Вторым признаком классификации многокритериальных задач является вид требуемого результата решения задачи. По этому признаку выделим следующие классы многокритериальных задач:
a) задачи, в которых необходимо выделить из множества объектов один наиболее предпочтительный объект (получить одно наиболее предпочтительное решение). В некоторых случаях может быть выделено не одно, а подмножество эквивалентных и наиболее предпочтительных объектов. Постановка задачи выделения наиболее предпочтительного объекта может быть как для дискретных, так и для непрерывных мно-
гокритериальных задач;
b)задачи, в которых необходимо упорядочить многокритериальные объекты. Постановка многокритериальной задачи в таком виде чаще всего имеет место для дискретных МКЗ, например, упорядочить по предпочтению варианты технических систем, по качеству — образцы продукции;
c)задачи, в которых требуется дать оценку полезности (качества) объектов по шкале интервалов. Другими словами, необходимо построить функцию полезности U(k1,...,km). Очевидно, что такая постановка задачи может быть как для дискретных, так и для непрерывных МКЗ;
d)задачи, в которых требуется выделить подмножество эффективных (конкурирующих) объектов. Такие подмножества называют оптимальными по Парето.
Чтобы говорить об эффективных объектах, надо ввести понятие доминируемого объекта.
Определение 1.1. Объект Вi доминирует объект Вl, если по всем критериям Вi предпочтительнее или эквивалентен Вl, и хотя бы по одному критерию строго предпо-
чтительнее. Объект Вi называют доминирующим, а Вl – доминируемым.
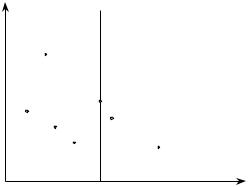
Если исключить из исходного множества доминируемые объекты, то останутся конкурирующие (эффективные). На рис.1.2, на примере двух критериев дискретной МКЗ, выделено подмножество эффективных объектов. В примере принято, что при увеличении k1 и k2 возрастает предпочтение объектов, В1, В3, В4 – доминируемые объекты.
Следует подчеркнуть, что прежде чем решать |
k2 |
|
|
|
|
дискретную задачу выделения наиболее предпочти- |
|
|
|
||
|
|
В2 |
Доминирующие |
|
|
тельного объекта, необходимо сначала выделить |
|
|
|
|
|
|
|
|
объекты |
|
|
|
|
|
|
|
|
подмножество эффективных объектов, так как иско- |
|
|
|
В5 |
|
мый объект может находиться только в этом под- |
|
|
|
|
|
|
|
|
|
|
|
|
|
В1 |
В6 |
|
|
множестве. |
|
|
В3 |
|
|
Для дискретных МКЗ выделение подмножества |
|
|
В4 |
В7 |
|
|
|
Доминируемые |
|
||
эффективных объектов тривиально, так как доста- |
|
|
|
|
|
|
|
объекты |
|
|
|
точно исключить из исходного множества домини- 0 0 |
Рис.1.2. Выделение эффективных |
k1 |
|||
руемые объекты. |
|
|
|
||
|
|
объектов |
|
|
|
Для непрерывных многокритериальных задач выделение подмножества эффективных объектов является самостоятельной и, следует
подчеркнуть, строго математической задачей. Причем, если область определения параметров x1,...,xn выпукла и целевые функции fj(x1,...,xn) (j=l, 2,...,m) монотонны по всем переменным, решение задачи определения наиболее предпочтительного объекта будет принадлежать подмножеству эффективных объектов. В настоящем пособии задача выделения эффективных объектов для непрерывных МКЗ не рассматривается.
Остановимся на характеристиках сложности многокритериальных задач. Среди них следует указать:
a)размерности задачи, т.е. число единичных критериев kj (j=l,...,m), а также количество объектов Bi (i=l,...,n) для дискретных МКЗ. Чем больше т и п, тем сложнее задача;
b)вид требуемого решения. По этому параметру задачи ранжируются по сложности следующим образом:
оценка объектов (самая сложная задача); упорядочение объектов по предпочтению;
выделение наиболее предпочтительного объекта;
c) уровень статистической взаимосвязи критериев, определяемый коэффициентом множественной корреляции критериев. В качестве такого коэффициента используем коэффициент согласия, применяемый в экспертных методах.
Пусть для дискретной МКЗ задана матрица значений критериев |
k j |
. На основе зна- |
|
i |
|
чений каждого критерия проранжируем объекты (варианты), тем самым перейдем от
матрицы |
k j |
к матрице рангов |
R j |
размерности n m, каждый столбец которой будет |
|
i |
|
i |
|
содержать ранги объектов по критерию kj.
Для расчета коэффициента согласия вычислим сначала:
m |
|
|
n |
|
Ri Rij |
, (i |
1, n |
) и S [Ri R]2 |
, где R m (n 1) / |
j 1 |
|
|
i 1 |
|
Коэффициент согласия определяется по формуле:
E |
|
|
12 S |
, |
|
|
m |
||
|
|
|
|
|
2 |
(n |
3 |
n) m Tj |
|
m |
|
|
||
|
|
|
j 1 |
|
2
.
где Tj, – поправки на связанные ранги, которые могут появиться в случае равенства значений критерия kj для нескольких объектов.
Данные поправки рассчитываются по формуле:
где
t |
i |
|
j |
||
|
|
n |
|
|
|
|
|
j |
|
|
|
|
T j |
i |
) |
3 |
i |
] |
[(t j |
|
t j |
i1
–число повторений ранга i, т.е. число объектов, у которых одинаковое значение
критерия kj.
Коэффициент согласия изменяется в интервале [0;1]. Коэффициент Е равен единице, если по всем критериям объекты одинаково упорядочены. Это соответствует случаю, когда один из объектов (имеющий первый ранг по всем критериям) доминирует все остальные, объект с рангом 2 доминирует все последующие и т.д. В этом тривиальном случае автоматически выделяется наиболее предпочтительный объект, кроме того, все объекты упорядочиваются по предпочтению. Конечно, задачи, для которых коэффициент согласия близок к единице, являются простыми в решении и, напротив, задачи, для которых Е мало, более сложны.
Перечисленные характеристики объективно отражают сложность задач. Вместе с тем, сложность задачи зависит от субъективных факторов: насколько она правильно и точно понимается ЛПР, т.е. насколько оно подготовлено к ее решению. Успешно решать задачу может лишь ЛПР, хорошо знающее объект исследования, понимающее цель задачи (цель принятия решения), в противном случае не будет получено удовлетворительного результата.
ПРОБЛЕМЫ РЕШЕНИЯ МКЗ
Основная проблема в решении МКЗ заключается в неоднородности пространства критериев, так как единичные критерии измеряются в различных единицах измерения. Поэтому в большинстве методов осуществляется переход от физических единиц к
относительным единицам измерения (uij ) , например, с использованием функций пере-
вода. Процедуры перехода к относительным единицам отличаются в разных методах, поэтому они будут описаны при изложении методов.

Следует подчеркнуть, что проблема однородности пространства критериев не решается полностью только переходом к относительным единицам, так как сравнить два объекта в пространстве критериев не представляется возможным. Поэтому необходимо также определить важность критериев (коэффициенты относительной важности)
W j , ( j 1, m) .
Коэффициенты Wj задаются ЛПР (или экспертами) и отражают его структуру предпочтений. В некоторых случаях при определении Wj используется информационный подход, суть которого в том, что более информативному критерию придается большее значение Wj.
Например, если некоторый критерий принимает одно и то же значение для всех рассматриваемых объектов (вариантов решений), то естественно считать, что данный критерий не информативен с точки зрения выбора решения, значит, важность такого критерия можно считать малой. В качестве меры информативности критерия рекомен-
дуется использовать: |
|
|
|
|
|
а) |
V j S j |
/ M (k j |
) |
, |
(1.1) |
где Sj — среднеквадратическое отклонение значений критерия, M(kj) — среднее значение критерия. Чем больше Vj, тем более информативен критерий;
б)
|
n |
n |
|
n |
|
hj |
i |
i |
i |
i |
) |
(u j |
/ u j |
) ln( u j |
/ u j |
||
|
i 1 |
i 1 |
|
i 1 |
|
(1.2)
где uij - значения критерия объекта i в относительных единицах. Выражение (1.2) сов-
падает с формулой для энтропии, а интерпретация hj следующая: чем меньше значение hj , тем больше разброс критерия, и, значит, он более информативен.
Далее надо отметить проблему агрегирования множества критериев в скаляр. В большинстве методов эта проблема решается тем или иным способом, но в некоторых методах она снимается путем введения определенного принципа выбора наиболее предпочтительного объекта (решения).
В отдельных методах проблемы неоднородности пространства критериев и агрегирования решаются путем сведения единиц измерения всех критериев к одной. Часто в экономических задачах такой единицей служит денежная единица (рубль). Тем самым стараются свести векторную многокритериальную задачу к скалярной (см. метод уступок).
Другой важной проблемой решения МКЗ является оценка доверия к получаемому решению. Дело в том, что при решении задач используется субъективная информация, поэтому у ЛПР возникает недоверие к результату.
Степень доверия к результату может быть оценена через его устойчивость по отношению к субъективным данным, используемым в методах (коэффициенты Wj, процедуры перехода к относительным единицам и т.д.). Если, например, при изменении Wj в качестве наиболее предпочтительного выделяется один и тот же объект, т.е. результат устойчив по отношению к Wj, то доверие к выделенному объекту выше.
Следует особо сказать об исследовании устойчивости результата по отношению к используемым методам решения МКЗ. Так как в каждом из методов используются различные идеи (подходы), то и результаты решения одной и той же задачи разными методами могут отличаться. Если же при использовании нескольких методов выделяется один и тот же наиболее предпочтительный объект, т.е. результат устойчив по отношению к методам, то доверие к полученному решению, конечно, высокое.
Говоря об устойчивости решения МКЗ, необходимо сказать о взаимозависимости
устойчивости и взаимосвязи исходных данных для дискретных МКЗ (матрица значений единичных критериев по всем объектам). Если критерии статистически взаимосвязаны между собой (коэффициент множественной корреляции принимает большое значение), то, как указывалось ранее, задача будет простой, и, значит, результат будет более устойчив как по отношению к субъективным данным, так и по отношению к методам решения.
КЛАССИФИКАЦИЯ МЕТОДОВ РЕШЕНИЯ МКЗ
Прежде чем переходить к методам, рассмотрим сначала подходы к решению МКЗ, каждый из которых характеризует класс методов.
Использование max-min-принципа выбора наиболее предпочтительного объекта. В
этих методах принципы выбора применяются к критериям в относительных единицах. Рассмотрим использование данного принципа для решения дискретных и непрерывных задач.
Пусть поставлена дискретная МКЗ, т.е. задана матрица относительных значений
критериев |
u j |
(i 1,..., n; j 1,..., m) |
(табл.1.1.). |
|
|
|
|
|
|||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
|
|
|
Относительные значения критериев |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариан- |
|
k1 |
|
k2 |
k3 |
k4 |
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ты |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
0.35 |
|
0.60 |
0.80 |
0.25 |
|
0.25 |
|
|
|
В2 |
|
0.20 |
|
0.80 |
0.50 |
0.70 |
|
0.20 |
|
|
|
В3 |
|
0.40 |
|
0.50 |
0.40 |
0.20 |
|
0.20 |
|
|
|
В4 |
|
0.30 |
|
0.70 |
0.60 |
0.40 |
|
0.30 |
|
|
|
В5 |
|
0.70 |
|
0.25 |
0.50 |
0.80 |
|
0.25 |
|
Оценка каждого объекта (варианта) производится по минимальному значению из
всех критериев u |
i |
min u j |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
j |
max u |
|
max min u j |
. В |
|
Наиболее предпочтительный объект выбирается из принципа |
|
||||||
|
|
|
|
i |
|
i |
|
|
|
|
i |
|
i |
j |
|
рассматриваемом примере это объект № 4.
Использование данного принципа для задач векторной оптимизации также рассмотрим на примере. Пусть имеется управляемый параметр x, область изменения которого [0;10]. Выбор значения x осуществляется с учетом трех критериев:
k1 |
3x 10; k2 4 x 2 ; k3 |
e 0.2 x . |
|
|
|
Для перехода к относительным единицам определим области их возможных значе- |
|||
ний: |
|
|
|
|
|
|
min k1 =10; min k2 =0; min k3 = e-2 |
; |
|
|
|
max k1 =40; max k2 =400; |
max k3 =1. |
|
|
В примере для перехода к относительным единицам используем линейные функ- |
|||
ции. Определим |
для каждого критерия |
области |
допустимых значений: |
|
k1 |
16, k1 40, k2 0, k2 400, k3 0, k3 1. |
|
|
|
Переход к относительным единицам будет осуществляться в соответствии с выра-
жением
u |
|
(k |
|
k |
|
) /(k |
|
k |
|
), |
k |
|
[k |
|
, k |
|
]. |
|
j |
j |
j |
j |
j |
j |
j |
j |
|||||||||||
|
|
|
|
|
|
|
|
|
|
Единичные критерии в относительных единицах будут определяться в соответствии с выражениями:
u |
|
0 |
при x 2, |
u |
0.125( x 2) |
при 2 x 10; |
|||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
u |
|
0.01x |
2 |
, 0 |
x |
10; |
u |
|
e |
0.2 x |
, 0 |
x 10. |
|
2 |
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
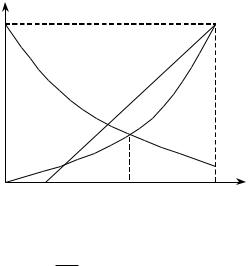
На рис.1.3 |
приведены зависимости критерия от |
||
параметра x. |
Принципу |
max min uj (x) соответствует |
|
|
|
x |
j |
значение х*, получаемое из уравнения u3 = u2; e-0.2x =
0.01x2.
uj(x) 1.0
u (x) |
u (x) |
3 |
1 |
При использовании описанного принципа ЛПР |
|
|
|
требуется задать лишь функции перевода критериев |
|
|
|
в относительные единицы, а проблемы определения |
|
|
|
коэффициентов важности критериев и агрегирова- |
0 |
|
|
ния критериев не возникают. |
0 |
||
|
|||
|
|
Как указывалось ранее, переход к относительным единицам не решает полностью проблему однородности пространства критериев, в котором следовало бы бора. Поэтому целесообразно задать коэффициенты W
предпочтительного объекта осуществлять по принципу
j
u2(x)
2 |
x* |
10 |
x |
Рис.1.3. Зависимость критериев от |
|
|
|
параметра x |
|
|
|
использовать принципы вы- , ( j 1, m) , а выбор наиболее
max min (W j uij ).
i j
Принцип max-min отражает осторожный подход (без риска) к выбору объекта по многим критериям. Наряду с этим принципом можно применять и другие, подобные тем, что используются в условиях неопределенности и риска, рассмотренные подробно в п.5.
Лексикографические методы основаны на понятии лексикографического порядка
(<L) векторов. Остановимся на нем подробнее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пусть заданы два вектора X {x1 ,..., xm } |
и |
Y {y1 |
,..., |
ym } |
. Между векторами устанав- |
||||||||||||||||
ливается бинарное отношение лексикографического порядка X<LY, если |
|||||||||||||||||||||
( x y ) (( x y |
) ( x |
2 |
y |
2 |
)) |
|
|
|
|
||||||||||||
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(( x |
y |
) ( x |
2 |
y |
2 |
) ( x |
3 |
y |
)) |
|
|
|
|||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
(( x |
y |
) ( x |
m 1 |
y |
m 1 |
) ( x |
m |
y |
m |
)). |
|||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отношение <L транзитивно, асимметрично, антирефлексивно.
Применительно к многокритериальным задачам для объектов i и l устанавливается отношение лексикографического порядка
Bl |
L |
Bi , если k l |
k i |
или (k l k i |
) (k l |
k i |
) или |
|||
|
1 |
|
1 |
|
1 |
1 |
2 |
2 |
|
|
(k l |
k i ) |
(k l |
|
k i |
) |
(k l |
k i ) |
|
|
|
1 |
1 |
m 1 |
m 1 |
|
m |
m |
|
|
||
(символ “ ” отражает предпочтение значения критерия). Другими словами, между объектами устанавливается отношение предпочтения, если выполняется отношение лексикографического порядка.
Очевидно, что критерии, при установлении лексикографического порядка должны быть упорядочены по важности, т.е. k1 – самый важный (значимый) критерий, k2 – следующий по важности, a km – наименее важный. После упорядочения по важности критериев, установление лексикографического порядка производится по следующей

процедуре:
a)устанавливается отношение предпочтения между объектами на основе значений первого (самого важного) критерия;
b)если значения первого критерия для нескольких объектов одинаково, то их упорядочивают между собой на основе значений второго по важности критерия. Если же найдутся одинаковые объекты по двум критериям, то они упорядочиваются на основе
значений k3 и т.д.
Чтобы обоснованно можно было использовать вышеописанную процедуру упорядочения объектов, необходимо, чтобы каждый критерий доминировал все последующие.
Условие доминирования k1 всех последующих означает, что порядок предпочтения объектов устанавливается только на основе k1 и не зависит от значений k2,…,km . Аналогично, k2 доминирует k3,...,km, если при равенстве значений k1, предпочтение объектов зависит только от k2 и не зависит от k3,...,km.
На первый взгляд, условие доминирования критериев является очень жестким и может выполняться в редких случаях. Однако, надо иметь в виду, что, сократив исходное множество объектов путем установления на критерии k j k ij k j , j 2, ,m та-
ких ограничений, чтобы
k |
|
k |
|
|
j |
j |
|||
|
|
были относительно небольшие значения, можно до-
биться того, что всё множество объектов мало будет отличаться друг от друга по критериям k2,…,km. Тем самым, предпочтение объектов будет определяться только критерием k1, т.е. он будет доминировать все последующие критерии.
Для непрерывных МКЗ выполнение условия доминирования критериев означает правомерность использования нижеописываемой процедуры решения задачи.
Пусть требуется определить параметры технической системы (x1,…,xn) с учетом критериев k1,…,km . Заданы целевые функции по каждому критерию fj(x1,…,xn), j = 1, 2,...,m, и определена область изменения параметров A(x1,…,xn).
Сначала упорядочиваются по важности единичные критерии, затем накладываются ограничения на значения критериев в виде
a |
j |
|
f |
j |
( x |
, , x |
n |
) b |
j |
|
|
|
1 |
|
|
или
f |
j |
( x |
, , x |
n |
) a |
j |
|
1 |
|
|
(1.3)
Неравенства, указывающие на допустимые значения k2,…,km , вводятся в систему ограничений A(x1,…,xn).
После чего в области A1(x1,…,xn) остаются только допустимые с точки зрения k2,…,km многокритериальные объекты, т.е. будет иметь место доминирование первым критерием остальных. Затем находятся параметры x1* , , xn* , оптимальные по k1.
Если же, решая оптимизационную задачу по k1, получили не одно, а множество (область) A2(x1,…,xn) параметров, для которых f1(x1,…,xn) равны, то необходимо решать оптимизационную задачу по критерию k2 на множестве A2(x1,…,xn) и т.д., пока не получим единственное решение.
Следует отметить, что, изменяя ограничения (1.3), можно сузить область изменения A до одного элемента, который и будет единственным допустимым и, в то же время, наиболее предпочтительным решением.
Для решения многокритериальных задач, в которых большое число неравнозначных единичных критериев, лексикографические методы используются для сокращения количества критериев. Для этого разбивают всё множество критериев на две группы: 1) k1,…,ks – критерии, по которым необходимо осуществлять выбор объектов; 2) ks+1,…,km – критерии, на значение которых можно только наложить ограничения. С
