
Лекции по ТПР / Метод PROMETHEE (5 объектов)
.pdf
Интерактивный метод PROMETHEE решения МКЗ
Метод получил свое название из аббревиатуры полного названия: Preference Ranking Organisation METHod for Enrichment Evaluations. В данном методе устанавливается отношение предпочтения между вариантами.
Метод рассмотрим на том же примере, что и метод смещенного идеала. Исходное множество вариантов:
Названи
еЗар. Удаленно Перспект
объекта |
Плата |
сть |
ивы |
Вариант 3 |
75 |
60 |
5 |
Вариант 4 |
60 |
50 |
9 |
Вариант 5 |
80 |
80 |
7 |
Вариант 7 |
80 |
70 |
4 |
Вариант 8 |
65 |
60 |
8 |
Вариант 6 исключен, т.к. он был доминируемым. Этап 1. Задание функций предпочтения.
Сравнение пар объектов i и l по каждому критерию осуществляется с использованием функций предпочтения H j (d ) , где d – разность значений критериев
двух объектов.
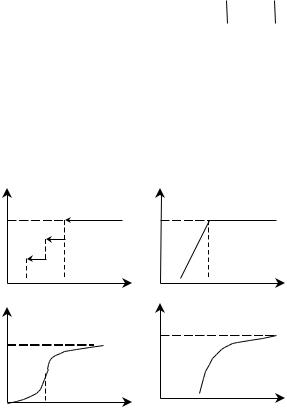
На рис.2.6 приведены несколько видов функций предпочтения. Как правило они имеют два параметра: р – порог безразличия, он отражает тот факт, что если разность  k ij k lj
k ij k lj  p j несущественна, то объекты по
p j несущественна, то объекты по
1
критерию j эквивалентны. При превышении разности
порогового |
значения |
p j |
между |
объектами |
устанавливается отношение предпочтения.
При превышении разности |
di,l |
k j |
|
|
j |
i |
|
k |
l |
|
j |
||
|
порога q
функция
предпочтения
H |
(d |
j |
) |
|
i,l |
||||
j |
|
|
1
,
что соответствует
«сильному предпочтению» варианта i по отношению к l варианту по j критерию.
При разности |
di,l |
в интервале от р до q функция |
|
j |
|
предпочтения меньше 1, что соответствует «Слабому предпочтению».
H(d) |
H(d) |
1,0 |
|
|
1,0 |
0,0 |
p |
d |
0,0 |
|
|
||
|
H(d) |
|
|
p |
q |
d |
H(d)
1,0 |
|
1,0 |
|
|
|
|
|
|
|
0,0 |
|
0,0 |
p |
d |
d |
|
|||
p |
|
|||
|
|
|
||
Рис.2.6. Типовые функции предпочтения |
|
|||
.
Таким образом, ЛПР должен задать для каждого критерия функцию предпочтения H j (d ) . Для
рассматриваемого примера в качестве функций
2

предпочтения используем линейные функции с участком безразличия.
Hj(d)
1 |
|
|
|
|
|
|
Сильное |
||
|
|
|
||
Область |
Слабое |
|
предпочтение |
|
безразличия |
|
|
|
|
предпочтение |
|
|
|
|
|
|
|
|
|
р |
|
q |
|
dj |
|
|
|
|
|
Линейная функция с участком безразличия
Значения пороговых параметров для критериев приведены ниже:
Критерий |
р |
q |
Зар. плата |
5 |
10 |
Удаленность |
10 |
20 |
Перспективы |
0 |
1 |
Этап |
2. Задание весов критериев. Возьмем в качестве |
||
весов те же, что в методе смещенного идеала: W1 = 0.4; |
|||
W2 = 0.3; W3 = 0.3. |
|
|
|
Этап |
3. Расчет индексов предпочтения |
|
i ,l , которые |
|
|||
|
m |
вычисляются по формуле: i,l Wj H j (di,jl ) , где W j |
|
|
j 1 |
m |
|
|
|
критериев W j |
1 . |
j 1 |
|
Результаты расчетов приведены ниже в таблице.
– веса
3
|
В3 |
В4 |
В5 |
В7 |
В8 |
Ф+ |
В3 |
0.0 |
0.4 |
0.3 |
0.3 |
0.4 |
1,4 |
В4 |
0.3 |
0.0 |
0.6 |
0.6 |
0.3 |
1,8 |
В5 |
0.3 |
0.4 |
0.0 |
0.3 |
0.4 |
1,4 |
В7 |
0.0 |
0.4 |
0.0 |
0.0 |
0.4 |
0,8 |
В8 |
0.3 |
0.0 |
0.6 |
0.3 |
0.0 |
1,2 |
Ф- |
0,9 |
1,2 |
1,5 |
1,5 |
1,5 |
|
Матрицу индексов предпочтения
|
i,l |
|
можно
представить в виде ориентированного графа предложений со взвешенными дугами, причем между каждой парой вершин устанавливаются две дуги с весами
i,l |
и l ,i . |
|
|
|
Этап 4. Определение коэффициентов предпочтени: |
||||
а) |
коэффициент предпочтения |
|
) |
рассчитывается |
(i |
||||
суммированием индексов предпочтения по строкам матрицы индексов предпочтения (всем выходящим дугам):
|
n |
|
i,l ; |
i |
|
|
l 1,l i |
б) коэффициент обратного предпочтения
суммирования по столбцам матрицы предпочтения (по всем входящим дугам):
|
n |
|
l ,i . |
i |
|
|
l 1,l i |
|
) |
путем |
(i |
индексов
|
|
|
|
|
|
(i 1, n) |
|||||
Вычисляемые коэффициенты i |
и i |
||||
являются информационной базой для упорпядочивания
4

вариантов и используются по-разному в модификациях метода.
Этап 5. Модификация 1 PROMETHEE
В этой модификации определяютяс бинарные отношения между каждой парой объектов:
|
|
|
i |
|
B |
l |
, если ( |
|
|
|
|
и |
|
|
|
|
) или ( |
|
|
и |
|||||
|
|
B |
|
|
i |
l |
|
i |
l |
i |
l |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
); |
|
|
|
|
|
|
|
|
i |
l ), или ( |
i l |
и i l |
|
|
||||||||||||||
|
|
B |
i |
~ B |
l |
(безразличны), если |
|
|
|
|
|
|
; |
||||||||||||
B |
|
|
|
i |
l |
и i |
l |
||||||||||||||||||
i |
не сравним с B |
l |
во всех других случаях. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Множество |
|
установленных |
бинарных |
отношений |
|||||||||||||||||||||
предпочтений отражает частичный порядок объектов. |
|||||||||||||||||||||||||
|
|
|
|
|
В3 |
|
|
|
В4 |
|
В5 |
|
|
В7 |
|
|
В8 |
|
|
|
|
|
|
||
В3 |
|
|
* |
|
|
|
N |
|
> |
|
|
> |
|
|
> |
|
|
|
|
|
|
|
|||
В4 |
|
|
N |
|
|
|
* |
|
> |
|
|
> |
|
|
> |
|
|
|
|
|
|
|
|||
В5 |
|
|
< |
|
|
|
< |
|
* |
|
|
> |
|
|
N |
|
|
|
|
|
|
|
|||
В7 |
|
|
< |
|
|
|
< |
|
< |
|
|
* |
|
|
< |
|
|
|
|
|
|
|
|||
В8 |
|
|
< |
|
|
|
< |
|
N |
|
|
> |
|
|
* |
|
|
|
|
|
|
|
|||
Из матрицы отношений можно видеть, что наиболее предпочтительным вариантом является вариант 5, т.к. он предпочтительней всех остальных.
Этап 6. Модификация 2 PROMETHEE
Данная модификация позволяет упорядочить объекты.
|
|
|
|
|||
Для этого вычисляется один коэффициент |
i (i 1,n) , |
|||||
характеризующий предпочтение |
B |
i |
по |
следующей |
||
|
|
|
|
|
|
|
формуле: i
Вариант
3
ii
Фi
0,5
.
5

Вариант
40,6
Вариант
5-0,1
Вариант
7-0,7
Вариант
8 -0,3
По значениям
|
i |
|
объекты упорядочиваются.
В4 > В3 >В5 >В7 > В8
Следует отметить, что не всегда предпочтительнее является модификация 2, так как больше информации о предпочтении объектов получает ЛПР, анализируя попарные отношения предпочтения. Так как этот метод является эвристическим, то получаемые результаты являются дополнительной информацией для ЛПР, и ему лучше иметь исходную информацию в виде множества бинарных отношений, чем агрегированную в модификации 2.
6
