2.2. Уравнение Лапласа в шаре

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SpecFunc.pdf

Скачиваний:

123

Добавлен:

05.06.2015

Размер:

2.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Задачи на уравнение Лапласа в шаре

(r2X0(r))0

sin θ sin θY0

Рассмотрим в сферических координатах

x = r sin θ cos ϕ,

y = r sin θ sin ϕ,

(2.2.1)

z = r cos θ.

уравнение Лапласа u = 0. Поскольку в

сферических координатах

u =

r2ur r+

(sin θuθ)θ+

uϕϕ,

r2 sin θ

r2 sin2 θ

то уравнение Лапласа принимает вид:

r2ur r

(2.2.2)

u ≡

(sin θuθ)θ

uϕϕ = 0.

r2 sin θ

r2 sin2 θ

Будем искать решение (2.2.2) методом разделения переменных.

Шаг 1. Поиск сферических гармоник

Пусть функция

U(r, θ, ϕ) = X(r)Y(θ, ϕ)

есть решение уравнения (2.2.2). Тогда

r2X0(r) 0 Y(θ, ϕ) + r2 sin θ

sin θYθ(θ, ϕ) θ X(r) + r2 sin2 θ Yϕϕ(θ, ϕ)X(r) = 0.

Поделим это равенство на X(r)Y(θ, ϕ) и умножим на r2:

(r2X0(r))0	1		sin θYθ(θ, ϕ) +	1	Yϕϕ(θ, ϕ)
(r2X0(r))0		sin θ	sin θYθ(θ, ϕ) +	sin2 θ	Yϕϕ(θ, ϕ)
	= −		θ
X(r)	= −		Y(θ, ϕ)

Так как слева стоит функция, зависящая только от r, а справа – функция, зависящая только от θ и ϕ, то равны они друг другу могут быть только в случае, когда они – константы. Точнее,

λ R :

(r2X0(r))0

sin θYθ(θ, ϕ) +

Yϕϕ(θ, ϕ)

sin θ

sin2 θ

= −

= λ.

X(r)

Y(θ, ϕ)

Отсюда для X(r) получаем уравнение

r2X00(r) + 2rX0(r) − λX(r) = 0,

(2.2.3)

а для функций Y – уравнение

sin θYθ(θ, ϕ) θ +

Yϕϕ(θ, ϕ) + λY(θ, ϕ) = 0.

(2.2.4)

sin θ

sin2 θ

Если решение уравнения (2.2.4) искать в виде

Y(θ, ϕ) = Θ(θ)Φ(ϕ),

(2.2.5)

то получим

Φ(ϕ) + sin2 θ Θ(θ)Φ00(ϕ) + λΘ(θ)Φ(ϕ) = 0.

sin θ sin θΘ0(θ) 0

-186-

2.2. УРАВНЕНИЕ ЛАПЛАСА В ШАРЕ

Поделим это равенство на	Θ(θ)Φ(ϕ)	.
	sin2 θ

	sin θ sin θΘ0(θ)		+ λ sin2 θ =	Φ00(ϕ)
				−		.
	Θ(θ)				Φ(ϕ)
Слева стоит функция, зависящая только от θ, а справа – только от ϕ, поэтому µ R :
sin θ sin θΘ0(θ) 0		+	λ sin2 θ − µ	Θ(θ) = 0,			(2.2.6)
	Φ00(ϕ) + µΦ(ϕ) = 0						(2.2.7)

Уравнение (2.2.7) необходимо дополнить условием периодичности, поскольку функция U(r, θ, ϕ), а следовательно и функция Φ должна быть непрерывной. Тогда для Φ(ϕ) получаем задачу:

	Φ00(ϕ) + µΦ(ϕ) = 0,
	Φ(ϕ + 2π) = Φ(ϕ).			(2.2.8)
Решим эту задачу. Общим решением уравнения Φ00(ϕ) + µΦ(ϕ) = 0 является функция
Φ(ϕ) = c1 + c2ϕ		при	µ = 0;
	Φ(ϕ) = c1 sh (βϕ) + c2 ch (βϕ)	при	µ = −β2 < 0;
	Φ(ϕ) = c1 sin (βϕ) + c2 cos (βϕ)	при	µ = β2	> 0.
Легко видеть, что	функции c1 sh (βϕ) + c2 ch (βϕ) ни при каких c1, 2			(кроме c1 = c2 = 0) не

удовлетворяют условию периодичности Φ(ϕ + 2π) = Φ(ϕ).

Всвою очередь, функции c1 + c2ϕ удовлетворяют условию периодичности только при c2 = 0.

Вто же время функция c1 sin (βϕ) + c2 cos (βϕ) удовлетворяет этому условию тогда и только

тогда, когда

µ = β2 = m2, m Z.

Мы будем рассматривать только m > 0, так как отрицательные значения m не дают новых µ или Φ(ϕ). А разрешая числу m принимать значение m = 0, мы включаем функцию Φ(ϕ) = const (являющуюся нетривиальным решением при λ = 0) в общую формулу нетривиальных решений (2.2.9).

Итак, функция (2.2.5) есть решение (2.2.4), то есть является сферической функцией тогда и только тогда, когда

Φ(ϕ) = c1 sin (mϕ) + c2 cos (mϕ) , m = 0, 1, 2, . . . ,		(2.2.9)
а функция Θ(θ) есть решение уравнения	+ λ sin2 θ − m2 Θ(θ) = 0.
sin θ sin θΘ0(θ) 0	+ λ sin2 θ − m2 Θ(θ) = 0.	(2.2.10)

В уравнении (2.2.10) сделаем замену переменой x = cos θ. Тогда для функции

P (x) = P (cos θ) ≡ Θ(θ)

получаем

Θ0(θ) = − sin θP 0(cos θ), Θ00(θ) = sin2 θP 00(cos θ) − cos θP 0(cos θ),

и уравнение (2.2.10) примет вид:

sin4 θP 00(x) − sin2 θ cos θP 0(x) − sin2 θ cos θP 0(x) + λ sin2 θ − m2 P (x) = 0.

c Д.С. Ткаченко

-187-

Задачи на уравнение Лапласа в шаре

Перепишем его, поделив сначала на sin2 θ, и учтём, что

cos θ = x, sin2 θ = 1 − x2 :

(1 − x2)P 00(x) − 2xP 0(x) + λ − 1 − x2 P (x) = 0.

Полученное уравнение совпадает с (2.1.15), стр. 184. Поэтому по теореме 2.1.5, стр. 185, все

ограниченные решения этой задачи описываются формулами

λ = n(n + 1),

n = 0, 1, 2, . . . ;

(2.2.11)

P (x) = Pnm(x) = 1 − x2

dmPn(x)

(2.2.12)

m = 0, n.

dxm

Поэтому все нетривиальные решения уравнения (2.2.10) имеют вид

Θmn(θ) = Pnm(cos θ),

(2.2.13)

n =

0, ∞

m = 0, n.

Наконец, с учётом (2.2.9), получаем, что

функция

U(r, θ, ϕ) = X(r)Y(θ, ϕ)

есть решение уравнения Лапласа тогда и только тогда, когда функция X(r) есть решение

уравнения

(2.2.3)

r2X00(r) + 2rX0(r) − λX(r) = 0,

при λ = n(n + 1), n =

0, ∞

, а функция Y(θ, ϕ) имеет вид

Y(θ, ϕ) = Ymn(θ, ϕ) = Pnm(cos θ) (c1 sin (mϕ) + c2 cos (mϕ)) ,

n =

0, ∞

m = 0, n.

(2.2.14)

Шаг 2. Решение уравнения (2.2.3)

Данное уравнение есть уравнение Эйлера, поскольку степень множителей r при всех производных функции X(r) равна порядку этих производных. Эти уравнения решаются при помощи замены

r = et, X(r) = X et

= y(t),

rX0(r) = y0(t), r2X00(r) = y00(t) − y0(t).

r =

−

et < 0

, поскольку в нашей задаче

(0, R)

. Для

Нам не надо рассматривать случай

новой функции y(t) при λ = n(n + 1), n =

получаем уравнение

0, ∞

y00(t) + y0(t) − n(n + 1)y(t) = 0, n =

0, ∞

Характеристическое уравнение для него имеет вид

Его корни:

κ2 + κ − n(n + 1) = 0.

−1 + √

κ1

1 + 4n2 + 4n

−1 + (2n + 1)

= n,

−1 − √

κ2

1 + 4n2 + 4n

−1 − (2n + 1)

−

и общее решение

y(t) = Aent + Be−(n+1)t.

Отсюда, так как et = r, общее решение уравнения (2.2.3) имеет вид

X(r) = Arn + Br−(n+1).

Ну а поскольку нас интересуют только ограниченные решения, то когда уравнение решается

-188-

2.2.УРАВНЕНИЕ ЛАПЛАСА В ШАРЕ

•в шаре, содержащем начало координат, B = 0 и


Xn(r) = rn,			n =	0, ∞		,				(2.2.15)
• во внешности шара, содержащего начало координат, A = 0 и
	1									(2.2.16)
Xn(r) =		,	n =		0, ∞		,
	rn+1
• в шаровом слое с центром в начале координат, A, B 6= 0 и
Xn(r) = Arn + Br−(n+1),										(2.2.17)
					n =			0, ∞	.

Шаг 3. Общее решение уравнения Лапласа в шаре

Нам осталось составить из полученных функций Xn (из равенства (2.2.15)), а также Ymn(θ, ϕ),

n = 0, ∞, m = 0, n ряд. Поскольку m меняется в пределах от 0 до n при каждом n, и только n меняется от 0 до ∞, то ряд можно составить только по n. Зато внутри ряда по n придётся ставить конечную сумму по m, формируя линейную комбинацию всех сферических гармоник степени n:

Ответ:

∞n

u(r, θ, ϕ) = Xn(r) Ymn(θ, ϕ) =

n=0 m=0

∞n

= rn	Pnm(cos θ) Amn cos (mϕ) + Bmn sin (mϕ) . (2.2.18)
n=0	m=0

Шаг 4. Общее решение уравнения Лапласа вне шара

Составим из полученных функций Xn (из равенства (2.2.17)), а также Ymn(θ, ϕ), n = 0, ∞, m = 0, n ряд. Здесь вся разница от задачи внутри шара состоит в том, что функции Xn(r) имеют вид (2.2.17), а не (2.2.15):

Ответ:

∞n

u(r, θ, ϕ) = Xn(r) Ymn(θ, ϕ) =

n=0 m=0

∞	1	n	Amn cos (mϕ) + Bmn sin (mϕ) . (2.2.19)
X		X
= n=0	rn+1	m=0 Pnm(cos θ)

Шаг 5. Общее решение уравнения Лапласа в шаровом слое

Поскольку в шаровом слое R1 < r < R2 ограниченными являются как функции (2.2.17), так и функции (2.2.15), ряд надо составлять из тех и других:

Ответ:

∞n

X X
u(r, θ, ϕ) =	rn Pnm(cos θ)	Amn cos (mϕ) + Bmn sin (mϕ) +
n=0	m=0
	∞	1	n	Cmn cos (mϕ) + Dmn sin (mϕ) . (2.2.20)
	X		X
	+ n=0	rn+1	m=0 Pnm(cos θ)

c Д.С. Ткаченко

-189-

Задачи на уравнение Лапласа в шаре

2.3. № 788 а)

Определить стационарное распределение температуры u(r, θ) в однородном шаре радиуса R для случая, когда поверхность шара имеет температуру:

u(R, θ) = f(θ) =	T2	,
	T1	,

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

(r2ur)r +

u ≡

sin θuθ θ

uϕϕ

= 0,

r2 sin θ

r2 sin2 θ

u(0, θ)

< ,

z}|{

∞

θ < α;

u(R, θ) = f(θ) =

T2,

α < θ 6 π.

0 6 θ < α; α < θ 6 π.

0 6 r < R, 0 < θ < π;

(2.3.1)

Повторим с необходимыми упрощениями, вызванными тем, что в нашем случае искомое решение не зависит от ϕ, шаги 1 – 3 раздела 2.2.

Шаг 1. Поиск сферических гармоник, не зависящих от ϕ

Пусть функция

U(r, θ) = X(r)Y(θ)

есть решение уравнения

sin θuθ

u ≡

r2ur r +

= 0.

(2.3.2)

r2 sin θ

Тогда

r2X0(r) 0 Y(θ) + r2 sin θ sin θY0

(θ) 0

X(r) = 0.

r12

Поделим это равенство на X(r)Y(θ) и умножим на r2:

Так как слева стоит функция, зависящая только от r, а справа – функция, зависящая только от θ, то равны они друг другу могут быть только в случае, когда они – константы. Точнее,

λ R :

sin θY0(θ)

(r2X0(r))0

sin θ

= λ.

X(r)

−

Y(θ)

Отсюда для X(r) получаем уравнение

r2X00(r) + 2rX0(r) − λX(r) = 0,

(2.3.3)

а для функций Y – уравнение

(θ) 0

sin θ sin θY0

+ λY(θ) = 0.

Домножим на sin2 θ:

sin2 θY00(θ) + sin θ cos θY0(θ) + λ sin2 θY(θ) = 0.

(2.3.4)

-190-

№788 а)

Вуравнении (2.3.4) сделаем замену переменой x = cos θ. Тогда для функции

P (x) = P (cos θ) ≡ Y(θ)

получаем

Y0(θ) = − sin θP 0(cos θ), Y00(θ) = sin2 θP 00(cos θ) − cos θP 0(cos θ),

и уравнение (2.3.4) примет вид:

sin4 θP 00(x) − sin2 θ cos θP 0(x) − sin2 θ cos θP 0(x) + λ sin2 θP (x) = 0.

Перепишем его, поделив сначала на sin2 θ, и учтём, что

cos θ = x, sin2 θ = 1 − x2 :

(1 − x2)P 00(x) − 2xP 0(x) + λP (x) = 0.

Полученное уравнение совпадает с (2.1.1), стр. 183. Поэтому по теореме 2.1.1, стр. 183, все

ограниченные решения этой задачи описываются формулами
		λ = n(n + 1),	n = 0, 1, 2, . . . ;						(2.3.5)
	P (x) = Pn(x) − полиномы Лежандра.								(2.3.6)
Поэтому все нетривиальные ограниченные решения уравнения (2.3.4) имеют вид
									(2.3.7)
		Yn(θ) = Pn(cos θ),		n =	0, ∞		.		(2.3.7)
Итак, с учётом (2.3.3), получаем, что
функция
		U(r, θ) = X(r)Y(θ)
есть независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.3.2) тогда
и только тогда, когда функция X(r) есть решение уравнения
		r2X00(r) + 2rX0(r) − λX(r) = 0,							(2.3.3)
при λ = n(n + 1), n =		, а функция Y(θ) имеет вид
при λ = n(n + 1), n =	0, ∞	, а функция Y(θ) имеет вид
									(2.3.8)
	Y(θ) = Yn(θ) = Pn(cos θ),				n =	0, ∞		.	(2.3.8)

Шаг 2. Решение уравнения (2.3.3)

r = et, X(r) = X et = y(t),	rtX0(r) = y0(t), r2X00(r) = y00(t) − y0(t).
Нам не надо рассматривать случай r = −e < 0, поскольку в нашей задаче r (0, R). Для
новой функции y(t) при λ = n(n + 1),	n =	0, ∞	получаем уравнение

y00(t) + y0(t) − n(n + 1)y(t) = 0, n = 0, ∞.

Характеристическое уравнение для него имеет вид

κ2 + κ − n(n + 1) = 0.

c Д.С. Ткаченко

-191-

Задачи на уравнение Лапласа в шаре

Его корни:

−1 + √

κ1

1 + 4n2 + 4n

−1 + (2n + 1)

= n,

−1 − √

κ2

1 + 4n2 + 4n

−1 − (2n + 1)

−

и общее решение

y(t) = Aent + Be−(n+1)t.

Отсюда, так как et = r, общее решение уравнения (2.3.3) имеет вид

X(r) = Arn + Br−(n+1).

Ну а поскольку нас интересуют только ограниченные решения, то B = 0 и

Xn(r) = rn, n =

0, ∞

(2.3.9)

Составив из полученных функций ряд, получим что независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.3.2) имеет вид:

∞	∞
X	X	(2.3.10)
u(r, θ) = AnXn(r)Yn(θ) =	AnrnPn(cos θ), An R.	(2.3.10)
n=0	n=0

Шаг 3. Использование краевого условия

Для нахождения коэффициентов An используем краевое условие

u(R, θ) = f(θ).

По теореме 2.1.7, стр. 185,

f(θ, ϕ) разлагается в следующий ряд Фурье

f(θ, ϕ) =

∞

Pk(cos θ) +

Pkm(cos θ) (αkm cos(mϕ) + βkm sin(mϕ))# ,

αk0

k=0

m=1

2π

(k + m)!

2π

α =

2k + 1

(k − m)!

dϕ cos(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

2π

(k + m)!

2π

2k + 1

(k − m)!

dϕ sin(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

(2.3.11)

(2.3.12)

(2.3.13)

При этом

ряд

(2.6.16)

сходится

к f(θ, ϕ)

абсолютно и

равномерно на

θ [0, π], ϕ [0, 2π].

Поскольку в нашем случае функция f(θ) не зависит от ϕ, то

km =

−

( )

(cos

) sin

{

= 0

2π

(k + m)! Z0

2k + 1

m)!

f θ P m

θdθ

cos(mϕ)dϕ = 0,

m ,

2π

· (k + m)! Z0

2k + 1

− m)!

f(θ) P m (cos θ) sin θdθ

sin(mϕ)dϕ = 0.

}

-192-

№ 788 а)

Найдём αk0:

=2π

αk0 =

f(θ) Pk (cos θ) sin θdθ

{

= (2 + 1) f(θ) Pk (cos θ) sin θdθ.

2π

k! Z0

2k + 1

dϕ

Приравнивая ряды

∞

αk0

u(R, θ) =

AnRnPn(cos θ) =

Pk(cos θ) = f(θ),

n=0

k=0

видим, что они равны, если

An = 2Rn

= 2Rn

f(θ) Pn (cos θ) sin θdθ.

αn0

2n + 1

Ответ в общем виде:

∞

(2.3.14)

u(r, θ) =

AnXn(r)Yn(θ) =

AnrnPn(cos θ),

n=0

An = 22Rn

f(θ) Pn (cos θ) sin θdθ.

(2.3.15)

n + 1

Нам осталось вычислить An в данном конкретном случае, когда

f(θ) = T2

α < θ 6 π.

0 6 θ < α;

Поскольку

cos α

T1Pn (cos θ) sin θdθ = x = cos θ

= −T1

Pn (x) dx =

n > 1i =

= hпо рекуррентной формуле (2.1.6)

(2n + 1)Pn(x) = Pn0

+1(x) − Pn0

−1(x)

x=1

= 2n + 1

Pn0

+1(x) − Pn0

−1(x)

dx = 2n + 1 (Pn+1(x) − Pn−1(x)) x=cos α =

cos α

= hпо формуле (2.1.8)

Pn(1) = 1i =

(Pn−1(cos α) − Pn+1(cos α)) ,

2n + 1

x=cos α

T2Pn (cos θ) sin θdθ = аналогично = 2n + 1 (Pn+1(x) − Pn−1(x)) x= 1

−

= hпо формуле (2.1.8)

n >

1i =

Pn(−1) = (−1) ,

(Pn+1(cos α) − Pn−1(cos α)) ,

2n + 1

n > 1;

α						α	θ=α
Z						Z	θ=α
Z	T1P0	(cos θ) sin θdθ =	P0	(x) ≡ 1	= T1	Z	sin θdθ = −T1 cos θ θ=0	= T1 (1 − cos α) , n = 0;
0		h		i		0

c Д.С. Ткаченко

-193-

Задачи на уравнение Лапласа в шаре

θ=π

T2P0 (cos θ) sin θdθ =

P0(x) ≡ 1

= T2

sin θdθ = −T2 cos θ θ=α = T2 (1 + cos α) ,

n = 0,

получаем

An = 22Rn

f(θ) Pn (cos θ) sin θdθ =

n + 1

2n+1

(Pn+1(cos α) − Pn−1(cos α)) ,

при

n > 1;

2Rn ·

22n−+11

(T1

+ T2

+ (T2

T1) cos(α)) ,

при

n = 0.

Ответ:

−

u(r, θ) =

T1 + T2 + (T2

T1) cos(α)

T2 − T1

∞ (P

(cos α)

(cos α))

n P

(cos θ),

−

n=1

n+1

−

n−1

где Pn(x) – полиномы Лежандра (2.1.2).

2.4. № 788 б)

Определить стационарное распределение температуры u(r, θ) в однородном шаре радиуса R для случая, когда шар нагревается плоскопараллельным потоком тепла плотности q, падающим на его поверхность сверху, и отдаёт тепло со всей своей поверхности в окружающую среду в результате конвективного теплообмена. Температура среды равна T .

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

(r2ur)r

0 6 r < R, 0 < θ < π;

u ≡

sin θuθ

uϕϕ

= 0,

r2 sin θ

r2 sin2 θ

u(0, θ)

< ,

z}|{

(2.4.1)

∞

cos θ + hT,

θ <

;

π2

ur(R, θ) + hu(R, θ) = f1(θ) = hT,

< θ 6 π.

Шаг 0. Вид решения и упрощение краевого условия

Легко убрать в краевом условии выражение hT , если искать решение задачи (2.4.1) в виде

u(r, θ) = T + v(r, θ).

(2.4.2)

Тогда v(r, θ) есть, очевидно, решение следующей задачи:

		v	1	(r2vr) +			1	sin θvθ		= 0,
		v	2	(r2vr) +		2	sin θ	sin θvθ		= 0,
			r		r	r	sin θ		θ
	\|		\|	∞					q	cos θ,
									k	cos θ,
									k
vr(R, θ) + hv(R, θ) = f(θ) =									0,

0 6 r < R,

0 < θ < π;

(2.4.3)

0 6 θ < π2 ;

π2 < θ 6 π.

Повторим дословно шаги 1 – 2 номера № 788 а).

Шаг 1. Поиск сферических гармоник, не зависящих от ϕ

Пусть функция

U(r, θ) = X(r)Y(θ)

-194-

№ 788 б)

есть решение уравнения

sin θvθ θ

v ≡

r2vr

r +

= 0.

(2.4.4)

r2 sin θ

Тогда

sin θY0(θ) 0

r2X0(r)

0 Y(θ) +

X(r) = 0.

r2 sin θ

Поделим это равенство на X(r)Y(θ) и умножим на r

(r2X0(r))0

sin θY0(θ) θ

−

sin θ

X(r)

Y(θ)

λ R :				1		sin θY0(θ)		0
	(r2X0(r))0
	(r2X0(r))0	=	−	sin θ					= λ.
		=							= λ.
	X(r)						Y(θ)
Отсюда для X(r) получаем уравнение
	r2X00(r) + 2rX0(r) − λX(r) = 0,									(2.4.5)
а для функций Y – уравнение
	sin θ sin θY0(θ) 0						+ λY(θ) = 0.
1
Домножим на sin2 θ:
sin2 θY00(θ) + sin θ cos θY0(θ) + λ sin2 θY(θ) = 0.										(2.4.6)
В уравнении (2.4.6) сделаем замену переменой x = cos θ. Тогда для функции
	P (x) = P (cos θ) ≡ Y(θ)
получаем
Y0(θ) = − sin θP 0(cos θ),			Y00(θ) = sin2 θP 00(cos θ) − cos θP 0(cos θ),
и уравнение (2.4.6) примет вид:
sin4 θP 00(x) − sin2 θ cos θP 0(x) − sin2 θ cos θP 0(x) + λ sin2 θP (x) = 0.
Перепишем его, поделив сначала на sin2 θ, и учтём, что
	cos θ = x,				sin2 θ = 1 − x2 :

(1 − x2)P 00(x) − 2xP 0(x) + λP (x) = 0.

Полученное уравнение совпадает с (2.1.1), стр. 183. Поэтому по теореме 2.1.1, стр. 183, все

ограниченные решения этой задачи описываются формулами
λ = n(n + 1),	n = 0, 1, 2, . . . ;	(2.4.7)
P (x) = Pn(x) − полиномы Лежандра.		(2.4.8)

c Д.С. Ткаченко

-195-

Задачи на уравнение Лапласа в шаре

Поэтому все нетривиальные ограниченные решения уравнения (2.4.6) имеют вид

							(2.4.9)
		Yn(θ) = Pn(cos θ),	n = 0, ∞.				(2.4.9)
Итак, с учётом (2.4.5), получаем, что
функция
		U(r, θ) = X(r)Y(θ)
есть независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.4.4) тогда
и только тогда, когда функция X(r) есть решение уравнения
		r2X00(r) + 2rX0(r) − λX(r) = 0,					(2.4.5)
при λ = n(n + 1), n =		, а функция Y(θ) имеет вид
при λ = n(n + 1), n =	0, ∞	, а функция Y(θ) имеет вид
							(2.4.10)
	Y(θ) = Yn(θ) = Pn(cos θ),			n =	0, ∞	.	(2.4.10)

Шаг 2. Решение уравнения (2.4.5)

r = et, X(r) = X et = y(t),

rtX0(r) = y0(t), r2X00(r) = y00(t) − y0(t).

Нам не надо рассматривать случай r = −e < 0, поскольку в нашей задаче r (0, R). Для

новой функции y(t) при λ = n(n + 1),

n =

0, ∞

получаем уравнение

y00(t) + y0(t) − n(n + 1)y(t) = 0, n =

0, ∞

Характеристическое уравнение для него имеет вид

κ2 + κ − n(n + 1) = 0.

Его корни:

−1 + √

κ1

1 + 4n2 + 4n

−1 + (2n + 1)

= n,

−1 − √

−1 − (2n + 1)

κ2

1 + 4n2 + 4n

−

и общее решение

y(t) = Aent + Be−(n+1)t.

Отсюда, так как et = r, общее решение уравнения (2.4.5) имеет вид

X(r) = Arn + Br−(n+1).

Ну а поскольку нас интересуют только ограниченные решения, то B = 0 и

Xn(r) = rn, n =

0, ∞

(2.4.11)

Составив из полученных функций ряд, получим что независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.4.4) имеет вид:

∞	∞
X	X	(2.4.12)
v(r, θ) = AnXn(r)Yn(θ) =	AnrnPn(cos θ), An R.	(2.4.12)
n=0	n=0

-196-

№ 788 б)

Шаг 3. Использование краевого условия

Для нахождения коэффициентов An используем краевое условие

vr(R, θ) + hv(R, θ) = f(θ).

По теореме 2.1.7, стр. 185,

f(θ, ϕ) разлагается в следующий ряд Фурье

f(θ, ϕ) =

∞

Pk(cos θ) +

Pkm(cos θ) (αkm cos(mϕ) + βkm sin(mϕ))# ,

αk0

k=0

m=1

2π

(k + m)!

2π

α =

2k + 1

(k − m)!

dϕ cos(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

2π

(k + m)!

2π

2k + 1

(k − m)!

dϕ sin(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

(2.4.13)

(2.4.14)

(2.4.15)

При этом

ряд

(2.6.16)

сходится

f(θ, ϕ)

абсолютно

равномерно на

θ [0, π], ϕ [0, 2π].

Поскольку в нашем случае функция f(θ) не зависит от ϕ, то

km =

−

( )

(cos

) sin

{

= 0

2π

(k + m)! Z0

2k + 1

m)!

f θ P m

θdθ

cos(mϕ)dϕ = 0,

m ,

2π

· (k + m)! Z0

2k + 1

− m)!

f(θ) P m (cos θ) sin θdθ

sin(mϕ)dϕ = 0.

Найдём αk0:

}

=2π

αk0 =

f(θ) Pk (cos θ) sin θdθ

{

= (2 + 1)

f(θ) Pk (cos θ) sin θdθ.

2π

k! Z0

2k + 1

dϕ

Приравнивая ряды

vr(R, θ) + hv(R, θ) = hA0

∞

∞ αk0

Pk(cos θ) = f(θ),

+ n=1 R

+ h AnRnPn(cos θ) = k=0

видим, что они равны, если

An = 2 (n + hR) Rn−1 =

2 (n + hR) Rn−1

f(θ) Pn (cos θ) sin θdθ,

n = 0, ∞.

αn0

2n + 1

Ответ в общем виде:

∞

AnrnPn(cos θ),

(2.4.16)

v(r, θ) =

AnXn(r)Yn(θ) =

n=0

An = 2 (n + hR) Rn−1

f(θ) Pn (cos θ) sin θdθ.

(2.4.17)

2n + 1

c Д.С. Ткаченко

-197-

Задачи на уравнение Лапласа в шаре

Нам осталось вычислить An в данном конкретном случае, когда

	kq cos θ,	0 6 θ < π2 ;
	0,	π2 < θ 6 π.
f(θ) =

Поскольку

Z Z

Pn (cos θ) sin θdθ =

x = cos θ

= −

Pn (x) dx =

n > 1i =

= hпо рекуррентной формуле (2.1.6)

(2n + 1)Pn(x) = Pn0

+1(x) − Pn0

−1(x)

−

Pn+1(x) − Pn−1(x) + c,

(2.4.18)

2n + 1

то при n > 2

cos θPn (cos θ) sin θdθ = x = cos θ = Z

xPn (x) dx =

по частям =

x (Pn+1(x) − Pn−1(x))

x=1

(x)

(x)) dx =

−

x=0

−

2n + 1

2n + 1 Z

n+1

n−1

(1) = 1

(n + 1)

hв силу равенства

и формулы (2.4.18) при

−

x=1

2n + 1

2n + 3

2n 1

x=0

Pn+2(x)

− Pn(x)

Pn(x) − Pn−2(x)

−

получаем при n = 2m + 1, m > 0:

2m+1

4m + 3

4m + 5

−

4m + 1

cos θP

(cos θ) sin θdθ =

P2m+3(x) − P2m+1

(x)

P2m+1(x) − P2m−1

(x)

а при n = 2m, так как

P2m+2(0) = −

(2m + 1)(2m + 2)

· P2m(0) = −

2m +

· P2m(0),

4(m + 1)2

2(m +

P2m−2(0) = −

2m2

· P2m(0) = −

· P2m(0),

m(2m − 1)

2m − 1

x=1

= 0,

x=0

(2.4.19)

(2.4.20)

-198-

№ 788 б)

имеем:

x=1

4m + 1

4m + 3

−

4m 1

x=0

cos θP

(cos θ) sin θdθ =

P2m+2(x) − P2m(x)

P2m(x)

− P2m−2(x)

−

P2m+2(0) − P2m(0)

P2m(0) − P2m−2(0)

−

hв силу (2.4.19) и (2.4.20)i

4m + 1

4m + 3

4m − 1

= − 4m + 1

4m + 3 ·

− 2(m + 1) − 1

− 4m − 1 · 1 + 2m − 1 =

P2m(0)

2m + 1

= 4m + 1 4m + 3 ·

2(m + 1) +

4m 1 · 2m

− 1 =

P2m(0)

4m + 3

= 4m + 1

2(m + 1) +

2m − 1

= 4m + 1

−

· 2(m + 1)(2m − 1) = 2(m + 1)(2m − 1)

P2m(0)

4m + 1

P2m(0)

Таким образом, при n > 2

An = 2 (n + hR) Rn−1

f(θ) Pn

(cos θ) sin θdθ = k ·2 (n + hR) Rn−1

cos(θ) Pn (cos θ) sin θdθ =

2n + 1

( k ·

2(2m+hR)R2m−1 · 2(m+1)(2m−1) ,

n = 2m,

m > 1.

P2m(0)

n = 2m + 1, m

> 1;

4m+1

Найдём теперь A0 и A1.

A0 = 2h

A1 = 2(1 + hR)

cos2 θ

θ= π2

f(θ) P0 (cos θ) sin θdθ =

cos θ sin θdθ = −

θ=0

2hk

4hk

f(θ) P1 (cos θ) sin θdθ = 2(1 + hR)

k cos2

θ sin θdθ =

0	0
= −	3q	·	cos3 θ	θ= π2
= −	2(1 + hR)k	·	3	θ=0

= 2(1 + hR)k .

Итак,

An = 2 (n + hR) Rn−1		π	f(θ) Pn (cos θ) sin θdθ =
An = 2 (n + hR) Rn−1		Z0	f(θ) Pn (cos θ) sin θdθ =
	2n + 1

			q	,
=		4hk		,
=		0,


			q
			2(1+hR)k		,
			q		4m+1	·	P2m(0)	,
	k ·			2(2m+hR)R2m−1		·	2(m+1)(2m−1)	,

Подставляя найденные An в (2.4.16)

∞

n = 0; n = 1;

n = 2m + 1, m > 1; n = 2m, m > 1.

X	X	(2.4.16)
v(r, θ) =	AnXn(r)Yn(θ) = AnrnPn(cos θ),	(2.4.16)
n=0	n=0

c Д.С. Ткаченко

-199-

				Задачи на уравнение Лапласа в шаре
и вспоминая, что u(r, θ) = T + v(r, θ), получаем
Ответ:
u(r, θ) = T +	q	+		q		qR ∞	(4m + 1)P m(0)		r	2m
u(r, θ) = T +	4hk	+	2(1 + hR)k		· r cos θ + 2k m=1 (2m + hR) (2m −2 1)(2m + 2)			R		P2m(cos θ)
						X

где Pn(x) – полиномы Лежандра (2.1.2).

2.5. № 788 в)

u(R, θ) = f(θ) =

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

0 6 θ < π2 ;

π2 < θ 6 π.

u ≡ r2 (r2ur)r + r2 sin θ

sin θuθ

+ r2 sin2 θ uϕϕ = 0,

0 6 r < R, 0 < θ < π;

< ,

z}|{

(2.5.1)

u(0, θ)

∞

θ <

;

π2

u(R, θ) = f(θ) =

Заметим, что эта задача – частный случай уже решённой нами в № 788 а) задачи (2.3.1) при

T1 = T , T2 = 0 и α = π2 . Воспользуемся результатом:

Ответ к № 788 а):

u(r, θ) =

T1 + T2 + (T2

T1) cos(α)

T2 − T1

∞

(cos α)

(cos α))

n P

(cos θ).

−

k=1

n+1

−

n−1

(2.5.2)

Подставив T1 = T , T2 = 0 и α =

π , получим:

∞

(2.5.3)

u(r, θ) = 2 −

k=1 (Pn+1(0) − Pn−1(0)) R

Pn(cos θ).

Далее, в силу (2.1.9),

P2m+1(0) = 0, P2m(0) =

(−1)m(2m)!

m > 0.

(2.1.9)

22m(m!)2

Поэтому, при n = 2m, m > 1

Pn+1(0) − Pn−1(0) = P2m+1(0) − P2m−1(0) = 0,

(2.5.4)

а при n = 2m + 1, m > 0

+ 1 P2m(0) =

Pn+1(0) − Pn−1(0) = P2m+2(0) − P2m(0) = − (2

4(m + 1)2

m + 1)(2m + 2)

	2m + 1			4m + 3
= −		+ 1	P2m(0) = −		P2m(0), (2.5.5)
	2(m + 1)			2(m + 1)

-200-

2.6. № 788 Г)

И, наконец, (2.5.3) переписывается в виде:

Ответ:

	T		T	∞	4m + 3
u(r, θ) =		+		X		P2m(0)
u(r, θ) =	2	+	2	m=0	2(m + 1)	P2m(0)
				m=0

где Pn(x) – полиномы Лежандра (2.1.2).

r 2m+1

P2m+1(cos θ),

2.6. № 788 г)

Определить стационарное распределение температуры u(r, θ) в однородном шаре радиуса R для случая, когда в шаре происходит объёмное тепловыделение с плотностью Q, а отвод тепла совершается через часть поверхности шара (0 6 θ 6 α) нормальным потоком постоянной плотности q, а остальная поверхность теплоизолирована.

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

= 0, 0 6 r < R, 0 < θ < π;

u +

≡

ur)r

sin θuθ

θ +

r2 sin θ

u(0, θ)

∞

(2.6.1)

θ < α;

(θ) =

−

ur(R, θ) = f1

α < θ 6 π.

Шаг 0. Вид решения и избавление от неоднородности в уравнении

Попробуем убрать неоднородность в уравнении, представив решение задачи (2.6.1) в виде

u(r, θ) = w(r) + v(r, θ) = Ar2 + B + v(r, θ),

(2.6.2)

где w(r) = Ar2 + B есть решение уравнения

w +

≡

r2w0 0 +

= 0.

(2.6.3)

Для w(r) = Ar

+ B это уравнение означает:

2A +

· 2Ar =

−

A = −

При этом константа B совершенно произвольна. Тогда

u(r, θ) = −

r2 + B + v(r, θ),

B R,

(2.6.4)

где v(r, θ) есть решение следующей задачи:

v(0≡, θ)

< ,

0 6 r < R, 0 < θ < π;

vr)r

r2 sin θ

sin θvθ

= 0,

∞

(2.6.5)

θ < α;

−Q

vr(R, θ) = f(θ) =

α < θ 6 π.

Прежде чем решать эту задачу, являющуюся аналогом задачи (2.3.1) номера № 788 а), учтём, что в шаре установился стационарный тепловой баланс, то есть что количество тепла, поступающего в шар, равно количеству тепла, выводимого из шара:

2π	π
Z	Z	(2.6.6)
dϕ	f(θ) sin θdθ = 0.	(2.6.6)

c Д.С. Ткаченко

-201-

		Задачи на уравнение Лапласа в шаре
Возьмём интегралы для данной функции f(θ):							Z	sin θdθ =
Z	dϕ Z	f(θ) sin θdθ = 2π − k		Z	sin θdθ + 6k		Z	sin θdθ =
2π	π		q	α		Q	π
0	0			0			0

= 2π − k · (1 − cos α) +

6k · 2

= 0 =

Поэтому

0 6 θ < α;

T1 =

−

1−cos α

f(θ) =

T2 =

α < θ 6 π.

Повторим дословно шаги 1 – 2 решения № 788 а):

Шаг 1. Поиск сферических гармоник, не зависящих от ϕ

Пусть функция

U(r, θ) = X(r)Y(θ)

есть решение уравнения

sin θvθ

v ≡

r2vr r +

= 0.

r2 sin θ

Тогда

r2X0(r) 0 Y(θ) + r2 sin θ sin θY0

(θ) 0

X(r) = 0.

r12

Поделим это равенство на X(r)Y(θ)

и умножим на r

q = 3(1 − cos α).

(2.6.7)

(r2X0(r))0		1	sin θY0(θ)
(r2X0(r))0		sin θ	sin θY0(θ)
	= −		θ
X(r)	= −		Y(θ)

λ R :				1		sin θY0(θ)		0
	(r2X0(r))0
	(r2X0(r))0	=	−		sin θ				= λ.
		=							= λ.
	X(r)						Y(θ)
Отсюда для X(r) получаем уравнение
	r2X00(r) + 2rX0(r) − λX(r) = 0,									(2.6.8)
а для функций Y – уравнение
	sin θ sin θY0(θ) 0						+ λY(θ) = 0.
1
Домножим на sin2 θ:
sin2 θY00(θ) + sin θ cos θY0(θ) + λ sin2 θY(θ) = 0.										(2.6.9)
В уравнении (2.6.9) сделаем замену переменой x = cos θ. Тогда для функции
	P (x) = P (cos θ) ≡ Y(θ)
получаем
Y0(θ) = − sin θP 0(cos θ),			Y00(θ) = sin2 θP 00(cos θ) − cos θP 0(cos θ),
				-202-

№ 788 г)

и уравнение (2.6.9) примет вид:

sin4 θP 00(x) − sin2 θ cos θP 0(x) − sin2 θ cos θP 0(x) + λ sin2 θP (x) = 0.

Перепишем его, поделив сначала на sin2 θ, и учтём, что

cos θ = x, sin2 θ = 1 − x2 :

(1 − x2)P 00(x) − 2xP 0(x) + λP (x) = 0.

Полученное уравнение совпадает с (2.1.1), стр. 183. Поэтому по теореме 2.1.1, стр. 183, все

ограниченные решения этой задачи описываются формулами
		λ = n(n + 1),	n = 0, 1, 2, . . . ;						(2.6.10)
	P (x) = Pn(x) − полиномы Лежандра.								(2.6.11)
Поэтому все нетривиальные ограниченные решения уравнения (2.6.9) имеют вид
									(2.6.12)
		Yn(θ) = Pn(cos θ),		n =	0, ∞		.		(2.6.12)
Итак, с учётом (2.6.8), получаем, что
функция
		U(r, θ) = X(r)Y(θ)
есть независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.6.7) тогда
и только тогда, когда функция X(r) есть решение уравнения
		r2X00(r) + 2rX0(r) − λX(r) = 0,							(2.6.8)
при λ = n(n + 1), n =		, а функция Y(θ) имеет вид
при λ = n(n + 1), n =	0, ∞	, а функция Y(θ) имеет вид
									(2.6.13)
	Y(θ) = Yn(θ) = Pn(cos θ),				n =	0, ∞		.	(2.6.13)

Шаг 2. Решение уравнения (2.6.8)

r = et, X(r) = X et = y(t),

rtX0(r) = y0(t), r2X00(r) = y00(t) − y0(t).

Нам не надо рассматривать случай r = −e < 0, поскольку в нашей задаче r (0, R). Для

новой функции y(t) при λ = n(n + 1),

n =

0, ∞

получаем уравнение

y00(t) + y0(t) − n(n + 1)y(t) = 0, n =

0, ∞

Характеристическое уравнение для него имеет вид

κ2 + κ − n(n + 1) = 0.

Его корни:

−1 + √

κ1

1 + 4n2 + 4n

−1 + (2n + 1)

= n,

−1 − √

−1 − (2n + 1)

κ2

1 + 4n2 + 4n

−

c Д.С. Ткаченко

-203-

Задачи на уравнение Лапласа в шаре

и общее решение

y(t) = Aent + Be−(n+1)t.

Отсюда, так как et = r, общее решение уравнения (2.6.8) имеет вид

X(r) = Arn + Br−(n+1).

Ну а поскольку нас интересуют только ограниченные решения, то B = 0 и

Xn(r) = rn, n =

0, ∞

(2.6.14)

Составив из полученных функций ряд, получим что независящее от ϕ ограниченное нетривиальное решение уравнения Лапласа (2.6.7) имеет вид:

∞	∞
X	X	(2.6.15)
v(r, θ) = AnXn(r)Yn(θ) =	AnrnPn(cos θ), An R.	(2.6.15)
n=0	n=0

Шаг 3. Использование краевого условия

Для нахождения коэффициентов An используем краевое условие

vr(R, θ) = f(θ).

По теореме 2.1.7, стр. 185,

f(θ, ϕ) разлагается в следующий ряд Фурье

f(θ, ϕ) =

∞

αk0

Pkm(cos θ) (αkm cos(mϕ) + βkm sin(mϕ))# ,

Pk(cos θ) +

k=0

m=1

2π

(k + m)!

2π

α =

2k + 1

(k − m)!

dϕ cos(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

2π

(k + m)!

2π

2k + 1

(k − m)!

dϕ sin(mϕ)

f(θ, ϕ) P m (cos θ) sin θdθ,

(2.6.16)

(2.6.17)

(2.6.18)

При этом

ряд

(2.6.16)

сходится

к f(θ, ϕ)

абсолютно и

равномерно на

θ [0, π], ϕ [0, 2π].

Поскольку в нашем случае функция f(θ) не зависит от ϕ, то

km =

−

( )

(cos

) sin

{

= 0

2π

(k + m)! Z0

2k + 1

m)!

f θ P m

θdθ

cos(mϕ)dϕ = 0,

m ,

2π

· (k + m)! Z0

2k + 1

− m)!

f(θ) P m (cos θ) sin θdθ

sin(mϕ)dϕ = 0.

Найдём αk0:

}

=2π

αk0 =			π	f(θ) Pk (cos θ) sin θdθ		z	}\|	{	= (2 + 1)
	2π		π		·	2π
	2π	· k! Z			·	Z
	2k + 1	k!					dϕ		k
							dϕ		k

f(θ) Pk (cos θ) sin θdθ.

-204-

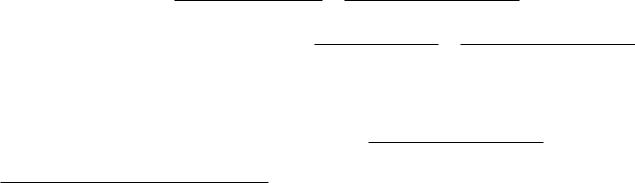
№ 788 г)

Приравнивая ряды


	∞						∞	αn0
	X						X			(2.6.19)
vr(R, θ) = nAnRn−1Pn(cos θ) =									Pn(cos θ) = f(θ),	(2.6.19)
	n=1						n=0	2
	n=1						n=0
видим, что они равны1, если
An = 2nRn−1 =			2nRn−1		π	f(θ) Pn (cos θ) sin θdθ, n N.
An = 2nRn−1 =			2nRn−1		Z0	f(θ) Pn (cos θ) sin θdθ, n N.
	αn0			2n + 1
Ответ в общем виде:
		∞			π		∞
		X			π		X			(2.6.20)
v(r, θ) =				AnXn(r)Yn(θ) =				AnrnPn(cos θ),		(2.6.20)
		n=0					n=0
	An =			2n + 1	Z0	f(θ) Pn	(cos θ) sin θdθ.			(2.6.21)

				2nRn−1

Нам осталось вычислить An в данном конкретном случае, когда

	T1 =	Q	1	−	2	,	0 6 θ < α;
		6k			1−cos α
f(θ) =	T2 =	Q	,				α < θ 6 π.
		6k

Поскольку

Z Z

Pn (cos θ) sin θdθ =

x = cos θ

= −

Pn (x) dx =

−1(x) n > 1i =

= hпо рекуррентной формуле (2.1.6)

(2n + 1)Pn(x) = Pn0

+1(x) − Pn0

−

Pn+1(x) − Pn−1(x) + c,

(2.6.22)

2n + 1

то при n > 1 имеем:

cos α

f(θ)Pn (cos θ) sin θdθ = x = cos θ = T2

Pn (x) dx+T1

Pn (x) dx =

в силу (2.6.22) =

−

−1

cos α

2n + 1

−

2n + 1

−

= T

Pn+1(−1)

− Pn−1(

Pn+1(cos α) − Pn−1(cos α)

−

2n + 1

−

2n + 1

Pn+1(1)

− Pn−1(1)

Pn+1(cos α) − Pn−1(cos α)

В силу равенств Pn(1) = 1 и Pn(−1) = (−1)n получаем

−

2n + 1

f(θ)P

(cos θ) sin θdθ = (T

)

Pn+1(cos α) − Pn−1(cos α)

1В силу (2.6.6), коэффициент α00 = 0. Заметим, что невыполнение условия (2.6.6), означающего равенство поступающего внутрь и выходящего наружу тепла, влечёт невозможность найти решение, ибо при α00 6= 0 равенство (2.6.19) выполнено быть не может.

c Д.С. Ткаченко

-205-

Задачи на уравнение Лапласа в шаре

откуда

2nRn−1

1 −

2nRn−1

(2.6.23)

2n + 1

f(θ) P

(cos θ) sin θdθ = (T

)

Pn+1(cos α) − Pn−1(cos α)

, n

При n = 0 коэффициент A0 может быть любым. Таким образом, для функции

∞

AnrnPn(cos θ)

v(r, θ) =

n=0

имеем:

v(r, θ) = A

(T1

T2) R

∞

Pn+1(cos α) − Pn−1

(cos α)

n P

(cos θ),

−2

n=1

(2.6.20)

и вспоминая, что u(r, θ) = −

+ B + v(r, θ), и что T1 − T2 = −

, получаем

3k(1−cos α)

Ответ:

u(r, θ) =

∞

Pn+1(cos α) − Pn−1(cos α)

n P

(cos θ) + const,

−

3k(1 − cos α) n=1

где Pn(x) – полиномы Лежандра (2.1.2).

2.7. № 788 д)

Определить стационарное распределение температуры u(r, θ) в однородном шаре радиуса R для случая, когда в шаре происходит объёмное тепловыделение с плотностью Q, а на поверхности – конвективный теплообмен по закону

ur(R, θ) + hu(R, θ) = f1(θ) = T + cos θ.

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

= 0, 0 6 r < R, 0 < θ < π;

u +

≡

ur)r

sin θuθ θ +

r2 sin θ

∞

u (R, θ) + hu(R, θ) = f (θ) = T + cos θ.

(2.7.1)

u(0, θ)

Шаг 0. Вид решения и избавление от неоднородности в уравнении

Попробуем убрать неоднородность в уравнении, представив решение задачи (2.7.1) в виде

u(r, θ) = w(r) + v(r, θ) = Ar2 + B + v(r, θ),							(2.7.2)
где w(r) = Ar2 + B есть решение задачи
	Q				Q
w +		≡	1	r2w0 0 +		= 0w0(R) + hw(R) = T.	(2.7.3)
	k		r2		k

Для w(r) = Ar2 + B уравнение (2.7.3) означает:

2		· 2Ar = −	Q	, =	A = −	Q
2A +							.
	r		k			6k
				-206-

c Д.С. Ткаченко

№ 788 д)

Тогда

w(r) = −

r2 + B.

Найдём константу B из краевого условия w0(R) + hw(R) = T :

−

R −

R2 + Bh = T

B =

R2 +

R +

3kh

Таким образом,

w(r) =

R2 − r2 +

R +

откуда

3kh

R2 − r2

u(r, θ) =

R +

+ v(r, θ),

3kh

где v(r, θ) есть решение следующей задачи:

v(0≡, θ) < ,

0 6 r < R,

vr)r +

r2 sin θ

sin θvθ

= 0,

0 < θ < π;

∞

(R, θ) + hv(R, θ) = f(θ) = cos θ.

(2.7.5)

Шаг 1.

Решение задачи

Эту задачу мы уже решили в № 788 б). Воспользуемся результатом:

Ответ в общем виде:

(2.7.4)

(2.7.5)

	∞				∞	(2.7.6)
	v(r, θ) =	AnXn(r)Yn(θ) =			AnrnPn(cos θ),
	n=0				n=0
	X		π		X
	2n + 1		Z0			(2.7.7)
An =				f(θ) Pn (cos θ) sin θdθ, n = 0, ∞.

	2 (n + hR) Rn−1

Нам осталось вычислить An в данном конкретном случае, когда f(θ) = cos θ.

И здесь важно заметить, что функция f(θ) ≡ P1(cos θ), а полиномы Pn(x) друг другу ортогональны (теорема 2.1.3), поэтому

An = 0 n 6= 1.

(2.7.8)

Осталось найти

cos3 θ

θ=π

A1 =

cos2 θ sin θdθ =

· −

θ=0 =

2 (1 + hR)

Таким образом, для v(r, θ) от всего ряда (2.7.6) осталось только одно слагаемое:

v(r, θ) = A1rP1(cos θ) ≡

r cos θ

1 + hR

Вспоминая, что

R2 − r2 +

u(r, θ) =

R +

+ v(r, θ),

получаем

3kh

Ответ:

R2 − r2 +

r cos θ

u(r, θ) =

R +

3kh

1 + hR

-207-

1 + hR.

(2.7.4)

Задачи на уравнение Лапласа в шаре

2.8. № 789

Определить стационарное распределение температуры u(r, θ) в теле, имеющем форму половины шара радиуса R, если сферическая часть его границы имеет температуру T , а плоское сонование – нулевую.

Записав эти условия математически, получим задачу:

Найти ограниченную функцию u(r, θ) из условий

0 6 r < R, 0 < θ <

ur)r

sin θuθ

= 0,

;

r2 sin θ

u(0≡, θ)

∞

(2.8.1)

θ <

;

u(R, θ) = f1(θ) = 0,

θ = π2 .

Шаг 0. Сведение к задаче в шаре

Поскольку существенная для нашего решения теорема 2.1.7, стр. 185, о разложений функций в ряд по сферическим гармоникам работает в шаре, а у нас в данной задаче – полушарие, надо попытаться свести задачу к аналогичной задаче в шаре.

Это несложно сделать, если вспомнить, как в подобной ситуации мы поступали с уравнениями теплопроводности и колебаний на полупрямой, когда методом продолжений доопределяли функции начальных условий на левую полупрямую

–нечётным образом, если краевое условие было I-го рода u(0, t) = 0, и

–чётным образом, если краевое условие было II-го рода ux(0, t) = 0.

Внашей задаче температура основания равна нулю, поэтому, по аналогии с первым случаем из метода продолжений, будем искать функцию u(r, θ) как решение следующей задачи в шаре:2

u(0≡, θ) < ,

0 6 r < R, 0 < θ < π;

ur)r

r2 sin θ

sin θuθ

= 0,

∞

(2.8.2)

θ <

;

u(R, θ) = f(θ) =

−

π2 < θ 6 π.

Шаг 1. Решение задачи (2.8.2)

Эту задачу мы уже решили в № 788 а), см. (2.3.1), стр. 190. Воспользуемся результатом Решением задачи

u(0≡, θ) < ,

0 6 r < R,

ur)r

r2 sin θ

sin θuθ

= 0,

0 < θ < π;

∞

(2.3.1)

θ < α;

u(R, θ) = f(θ) =

T2,

α < θ 6 π

является функция

u(r, θ) =

T1 + T2 + (T2 − T1) cos(α)

+ T2 − T1

∞

P (cos α)) r

n P (cos θ),

(P (cos α)

n+1

− n−1

(2.8.3)

n=1

2Этот подход является весьма естественным и с физической точки зрения: поскольку нас интересует стационарное распределение температуры, то есть состояние, в котором шар окажется, когда все тепловые процессы перестанут менять его температуру, то из соображений симметрии на сечении θ = π2 установится температура, равная среднему значению температур верхней и нижней полусфер.

-208-

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.06.2015895.72 Кб8SKETCH_UserGuide.pdf
#
04.06.2015511.46 Кб43Skhemy_Orlov.нов.doc
#
04.06.2015137.09 Кб59sostoyania_cheloveka_v_protsesse_truda.docx
#
18.11.2019296.96 Кб100SO_UI_U3-4_TestA.doc
#
05.06.2015696.53 Кб29Speak ehglish with us.pdf
#
05.06.20152.13 Mб123SpecFunc.pdf
#
08.01.202087.77 Кб0spetsializatsia_Avtosokhranennyy.docx
#
05.06.2015605.52 Кб36Spisok_opredeleny_k_ekzamenu_2014.pdf
#
04.08.201990.05 Кб6SPORY.docx
#
04.06.20153.1 Mб22Statistics.doc
#
26.09.2019275.46 Кб14STBDiIS шпоры1.doc