Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_DM_Teoria_Grafov_2y_semestr

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Хроматическое число

Дискретная математика: теория графов

Алгоритм приведения графа G к планарному

1)Найти все подграф, гомеоморфные K3,3 и K5 .

2)Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют.

3)Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).

Раскраска графов

Пусть		G V ,U			- некоторый граф и				S V1,V2	,...,Vk	- разбиение V

на k внутренне устойчивых множеств (разбиение означает, что
k
Vi	V			Vi Vj			i j
i 1			и			, если		). В этом случае говорят, что

вершины графа допускают раскраску в k цветов (цвета по
номерам 1,2,..., k ). Хроматическое число h G										- минимальное

значение k , которое допускает раскраску графа.

Хроматическое число пустого графа равно 1. h Kn n.

h K p,q 2.

Алгоритм нахождения раскраски (хроматического числа)

1)Выделить все пустые подграфы графа.

2)Построить таблицу покрытий вершин графа пустыми подграфами.

3)Найти минимальное покрытие вершин графа пустыми

Document from www.cyberfac.ru

- 41 -

Дискретная математика: теория графов

подграфами (мощность минимального покрытия – это h G , а само покрытие определяет раскраску).

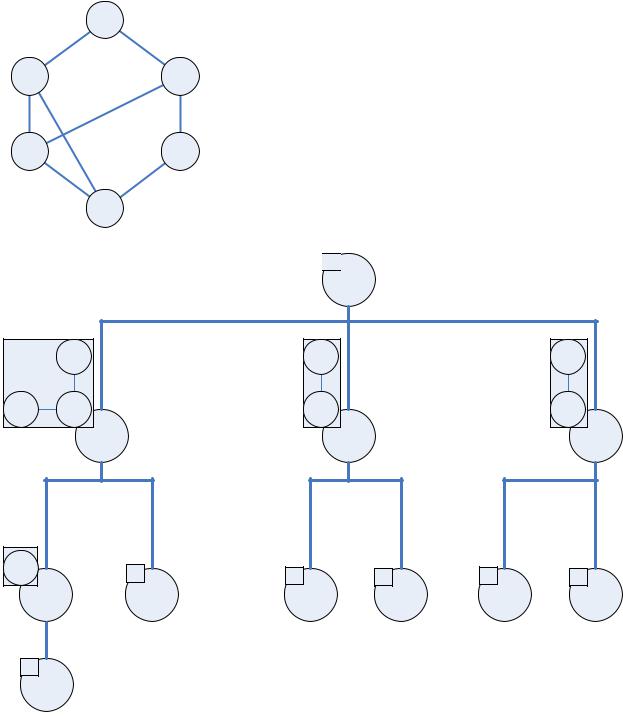
Пример

G1 x2 , x4 , x6 G2 x2 , x5 G3 x1 , x3 G4 x1 , x4 G5 x3 , x5

	x4
x6	x5	x2
		x2

x4		x1
x3	x1	x5	x3
	x1		x3

x6 x	x	x	x	x	x
4	5	3	4	1	5

Document from www.cyberfac.ru

- 42 -

Дискретная математика: теория графов

	G1	G2	G3	G4	G5
x1			1	1
x2	1	1				2
x3			1		1	x1
x4	1			1
x5		1			1	x6
x6	1					x6
x6	1					1
						1

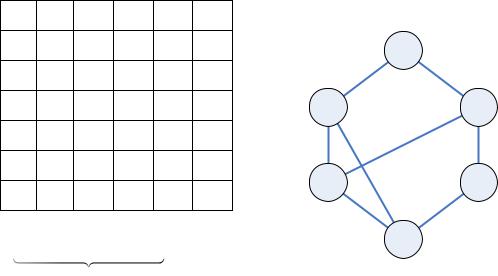
min G1,G3 ,G5	h G 3
одно из минимальных покрытий

Оценки хроматического числа

Теорема Кенига

Граф бихроматичен ( h G 2) тогда и только тогда, когда в G нет циклов нечетной длины.

Теорема

p G h G , где p G - плотность графа G .

3.
Теорема
h G S G 1, где S						G - степень графа G .
4.
Оценка Бержа
	V	h G	V	0	1	, где 0 - число внешней устойчивости графа




	0
	0

G .

Document from www.cyberfac.ru

- 43 -

другие два цвета.

Дискретная математика: теория графов

Теорема
h G h Ga h Gb , где G Ga Gb ,				Va Vb .
h G max h Ga ;h Gb		, где	G G	G	V V	.
		, где	a	b ,	a b	.
h G h Ga h Gb , где G Ga Gb ,				Va Vb .
h G min h Ga ;h Gb	, где		G G G
	, где		a	b .

Примеры

h C175 C174 ?

а) Графы не имеют общих вершин.

По теореме выше h C175 C174 h C175 h C174 3 2 5 . б) Графы имеют по одной общей вершине.

Отметим для нечетного цикла следующую раскраску: одна вершина в 3-й цвет, остальные в 1-й и 2-й цвета поочередно. На нашем графе вначале раскрасим в два цвета четный цикл (вместе с общей вершиной). Теперь рассмотрим нечетный цикл. В нем общая вершина оказалась закрашена каким-то цветом. Считаем этот цвет 3-им и закрашиваем все остальные вершины поочередно в два цвета (отличные от ранее выбранных, так как имеем граф суммы).

Итого использовали четыре цвета. h C175 C174 4.

в) Графы имеют по две общие, не смежные между собой вершины. Так как между двумя смежными вершинами в обоих графах

	174		87

	будет располагаться цепь длиной, по крайней мере, 2
			,

соединенная с аналогичной цепью в другой части графа всеми

возможными связями, то h C175 C174 4 . Для четырех цветов раскраска существует всегда: сначала раскрашиваем четный цикл в два цвета, затем оставшиеся цепи нечетного цикла закрашиваем в

h C175 C174 4 .

Алгоритм приближенной раскраски графа (алгоритм Ершова)

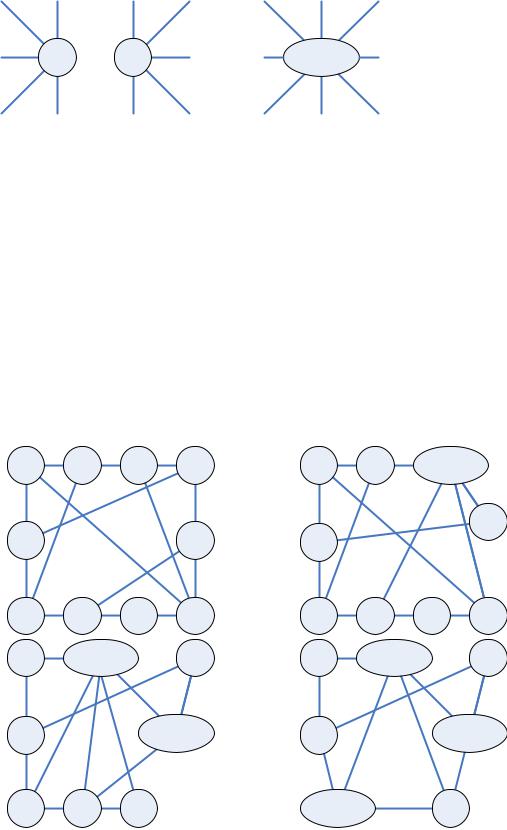
Алгоритм основан на стягивании несмежных вершин:

Document from www.cyberfac.ru

- 44 -

Дискретная математика: теория графов

v j

vivj vi vj

Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.

Замечание В первую очередь желательно стягивать те вершины, расстояние

между которыми четно.

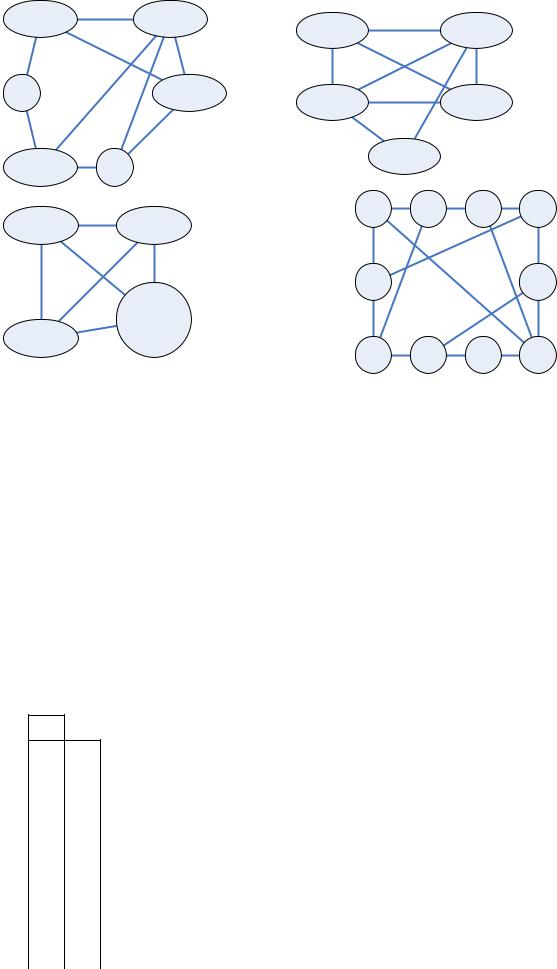
Пример
x9	x10	x1	x2
x8			x3	x1x3
x8			x3

x7	x6	x5	x4
x9	x4	x10	x2
		x1	x3	x5 x7
x8		x1	x3

x7	x6	x5

x9	x10	x1	x3
			x2	x4 x10
x8			x2
x8
x7	x6	x5	x4
x9	x4	x10	x2
		x1	x3	x2 x9
x8		x1	x3

x5	x7	x6

Document from www.cyberfac.ru

- 45 -

			Дискретная математика: теория графов
x2	x9	x4	x10			x2	x9	x4	x10
						x2	x9	x4	x10
										x1x3
					x6 x8					x x
x8			x1	x3	x6 x8					5 7
x8			x1	x3		x6	x8	x1	x3
						x6	x8	x1	x3
x5	x7	x6					x5	x7
x5	x7	x6
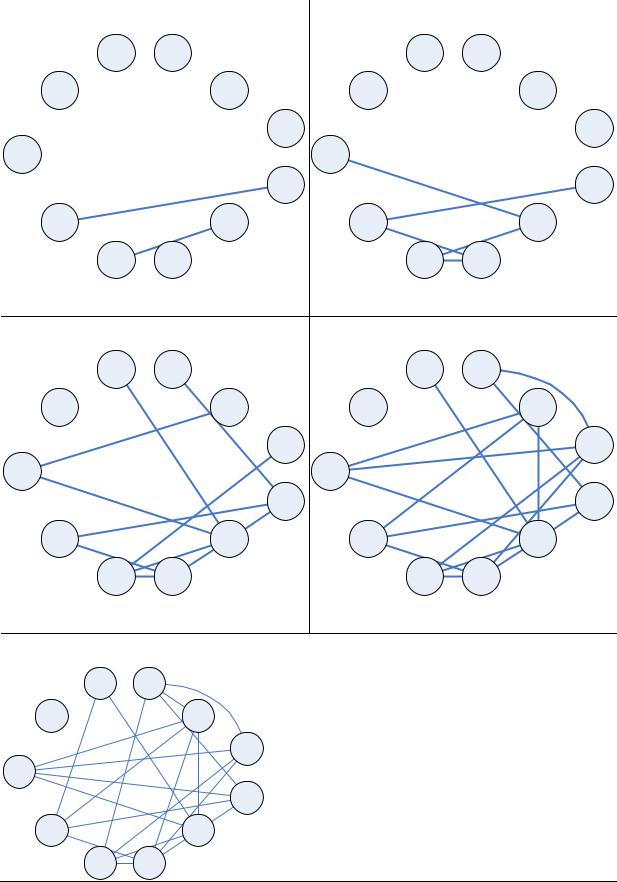
x2	x9	x4	x10				2	3	1	2
x2	x9	x4	x10
					h G 4		4			1
		x1	x3
x6	x8	x5	x7				1	4	1	3
							1	4	1	3

Задача

Есть 3 предприятия, на которых должны выпускаться 11 изделий. Каждый тип изделий должен выпускаться только на одном предприятии. При выпуске изделий разного типа

( a,b,c,d,e, f , g,h,i, j,k ) могут использоваться общие детали и материалы. Для каждой пары изделий указан процент общих деталей и материалов. Необходимо распределить изделия по предприятиям так, чтобы на одном предприятии выпускались детали с наибольшим процентом общих деталей. Критерий: Минимум общих поставок для изделий, выпускаемых на одном предприятии был как можно больше.

b55 b

c60 80 c

d	85	65	40	d
e	45	90	35	80	e
f	80	75	30	90	90	f
g							g
g	50	30	70	35	65	30	g
h	50	60	90	40	35	70	30	h
i	60	45	40	80	30	70	20	25	i
j	45	40	45	35	80	20	90	25	85	j
k	80	70	85	30	35	40	25	75	75	60

Document from www.cyberfac.ru

- 46 -

		Дискретная математика: теория графов
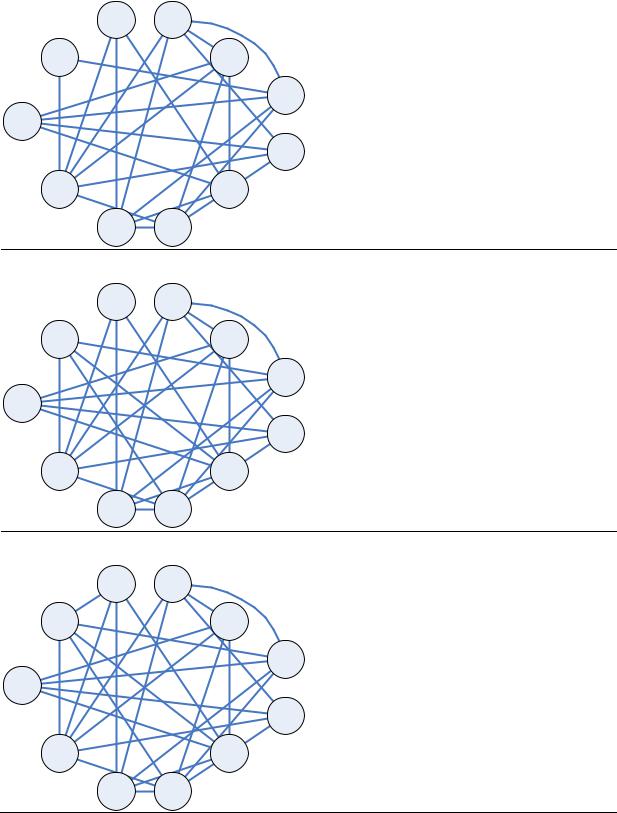
Граф несовместимости изделий G %
G	20%		G	25%
	b	c		b		c
	a	d		a		d
		e				e
k			k
		f				f
	j	g		j		g
	i	h		i		h
h G 20% 2			h G 25% 2
G	30%		G	35%
	b	c		b		c
	a	d		a		d
		e				e
k			k
		f				f
	j	g		j		g
	i	h		i		h
h G 30% 3			h G 35% 3
G	40%		h G 40% 3
	b	c	Раскраска:
	a	d	a	1, 2,3	f	1
			a	1, 2,3

		e	b	1, 2	g	3
			b	1, 2

k			c	2	h	2
		f	d	1	i	1
			d	1
	j	g	e	3	j	3
			e	3
	i	h			k	2

Document from www.cyberfac.ru

- 47 -

	Дискретная математика: теория графов

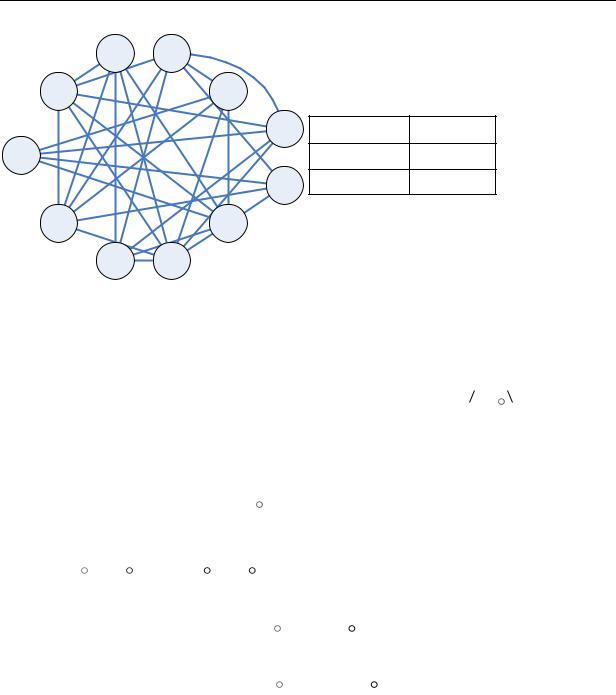
G 45%	h G 45% 3

	b	c	Раскраска:		f	1
	a	d	a	1, 2

			b	2	g	3

		e			h	2
k			c	2

			d	1	i	1
		f

			e	3	j	3

	j	g
					k	2

	i	h
G	50%		h G 50% 3
	b	c	Раскраска:		f	1
	a	d	a	1

			b	2	g	3

		e			h	2
k			c	2

			d	1	i	1
		f

			e	3	j	3

	j	g
					k	2

	i	h
G	55%		h G 55% 3
	b	c	Раскраска:		f	1
	a	d	a	1

			b	2	g	3

		e			h	2
k			c	2

			d	1	i	1
		f

			e	3	j	3

	j	g
					k	2

	i	h

Document from www.cyberfac.ru

- 48 -

Дискретная математика: теория графов

G 60%

	h G 60% 3
	Решение - G 55%
d
e	I предп.	a, d, f ,i
	II предп.	b,c, h, k
f	III предп.	e, g, j
g

Перечисление графов Группа. Группа подстановки

Группа – алгебра с одно бинарной операцией ( 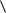A, 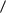), которая обладает следующими свойствами:

1)	замкнутость
	i	A	и	j A i	j A
			и
2)	ассоциативность
	i	j	k i j		k
3)	наличие нейтрального элемента
	0 A i A 0 i i					0 i
4)	существование обратного элемента
	для	A 1 A 1 1					0
	для

Группа подстановки. Пусть X x1, x2 , x3 . Подстановкой назовем

: X X .

Document from www.cyberfac.ru

- 49 -

Дискретная математика: теория графов

0	x	x	x
0	1	2	3
	x1	x2	x3
	x1		x2

		x	x
	0	1	1
0		x2 x2
		x	x
	0	x	x
	0	3	3

		x3
1	x	x
1	1	2
	x2	x1

1 x1x2 x3

2	x	x
2	1	2
	x3	x2

2 x1x3 x2

3	x	x
3	1	2
	x1	x3

2 x1 x2 x3

4	x	x
4	1	2
	x3	x1

4 x1x3 x2

0 x1 x2 x3

x
3	x1	x2
x3	x1	x2
x3
	x3
x
3	x	x
x1	1	2
	1	2
	x3
x
3	x	x
x2	1	2
	1	2
		x3
x	x1	x2
3	x1	x2
x2
	x3

	x	x	x
5	1	2	3	x1	x2
5	1	x3	x1	x1	x2
	x2	x3	x1

5 x1x2 x3	x3
5 x1x2 x3
A 0 , 1, 2 , 3 , 4 , 5
Операция: произведение подстановок		i	j ?
Операция: произведение подстановок

Document from www.cyberfac.ru

- 50 -

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.11.2019687.62 Кб9Lecture_1.doc
#
24.11.20192.22 Mб5Lecture_3.doc
#
01.05.2025499.71 Кб0LEC_FM_6320.doc
#
01.07.2025267.32 Кб0lek7.docx
#
10.07.2019973.01 Кб4Lektsia_4 (1).docx
#
05.06.20151.38 Mб10Lektsii_DM_Teoria_Grafov_2y_semestr.pdf
#
30.07.2019258.07 Кб5Lektsii_po_kulturologii.rtf
#
05.06.20151.32 Mб150lektsii_Telyaka_starshego.pdf
#
01.03.2025281.94 Кб1Lektsii_TP.docx
#
01.05.202541.6 Кб0LE_AU_2.docx
#
01.05.202556.78 Кб0LE_AU_4.docx

d	85	65	40	d
e	45	90	35	80	e
f	80	75	30	90	90	f
g							g
g	50	30	70	35	65	30	g
h	50	60	90	40	35	70	30	h
i	60	45	40	80	30	70	20	25	i
j	45	40	45	35	80	20	90	25	85	j
k	80	70	85	30	35	40	25	75	75	60

d	85	65	40	d
e	45	90	35	80	e
f	80	75	30	90	90	f
g							g
g	50	30	70	35	65	30	g
h	50	60	90	40	35	70	30	h
i	60	45	40	80	30	70	20	25	i
j	45	40	45	35	80	20	90	25	85	j
k	80	70	85	30	35	40	25	75	75	60

d	85	65	40	d
e	45	90	35	80	e
f	80	75	30	90	90	f
g							g
g	50	30	70	35	65	30	g
h	50	60	90	40	35	70	30	h
i	60	45	40	80	30	70	20	25	i
j	45	40	45	35	80	20	90	25	85	j
k	80	70	85	30	35	40	25	75	75	60