Lektsii_DM_Teoria_Grafov_2y_semestr

Дискретная математика: теория графов

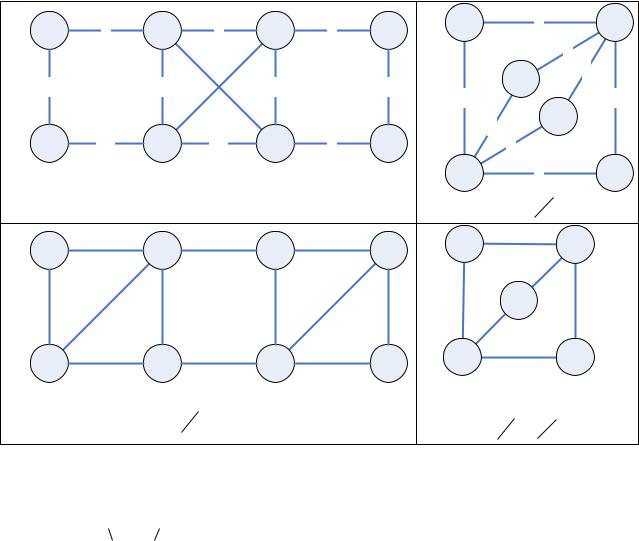
вершина-исток ( v ) вершина-сток ( v )

Каждая вершина в сети является компонентой сильной связности.

получена из орграфа путем сжатия каждой КСС в одну вершину.

Циклы в графе

Эйлеровы и Гамильтоновы циклы

Цикл в графе называется Эйлеровым, если любое ребро графа участвует в его образовании ровно один раз. Граф, содержащий Эйлеров цикл называется Эйлеровым.

Теорема Эйлера Граф является Эйлеровым тогда и только тогда, когда степени всех его вершин четные.

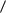Пусть G V ,U 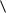- граф. Цикл в графе может быть записан в виде cj c u1 ,c u2 ,...,c uq , где

1, если ребро u участвует в образовании цикла c

c ui i j

0, в противном случае.

Дискретная математика: теория графов

Пример

Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа

G - мощность базисной системы циклов графа G .

G U G V G k G

G 8 6 1 3

Граф, у которого цикломатическое число равно 0, называется

деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.

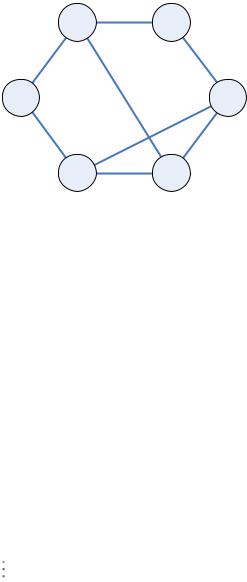
Дискретная математика: теория графов

Алгоритм нахождения базисной системы циклов

1. Получить остов графа (удалить G ребер; удаляемые ребра

называются хордами).

2. Добавляя к остову поочередно по одной хорде получаем базисную систему циклов.

Пример

Множество всех циклов графа: c1 c2

c1 c2 ... c

Число циклов в графе не превосходит 2 G 1.

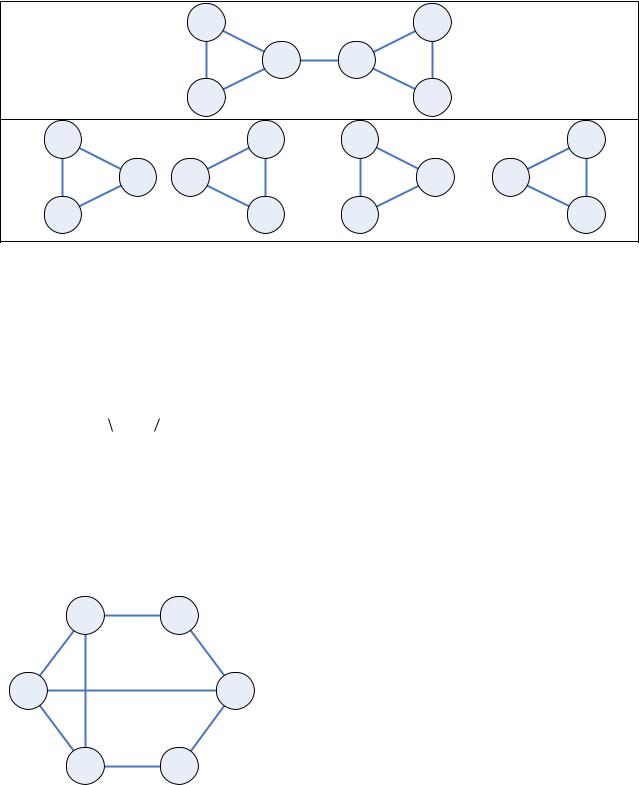
Дискретная математика: теория графов

Пример

Теорема Кенига Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины.

Разделяющие множества. Разрезы

Пусть G V ,U 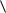- некоторый связный граф. Подмножество ребер

графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.

цикл разрез (коцикл)

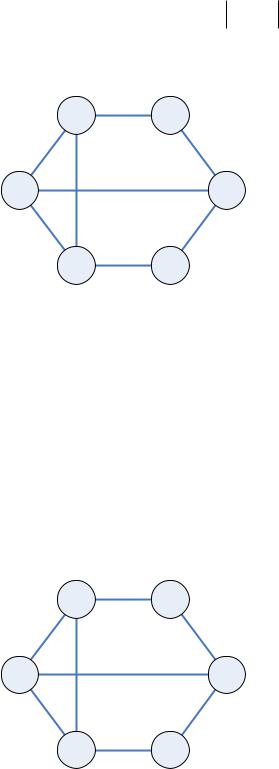
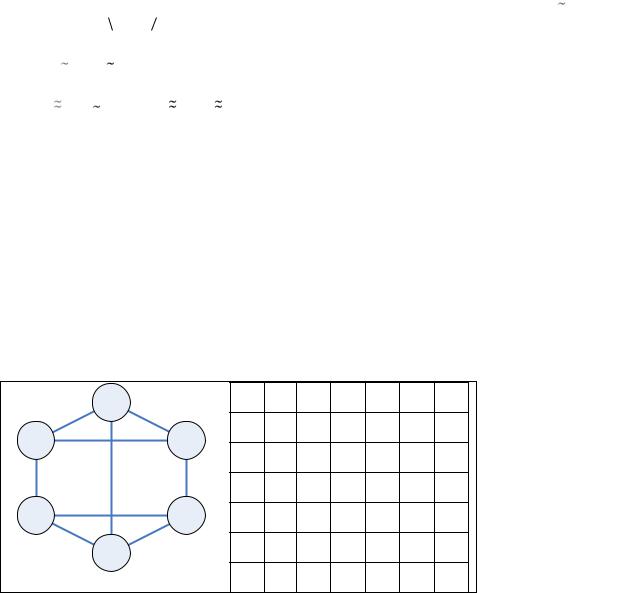
Алгоритм нахождения базисной системы разрезов

1.Построить остов графа G .

2.Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам.

Пример

Дискретная математика: теория графов

Число коциклов в графе равно 2 G 1.

Устойчивость графа

Внешняя устойчивость графа

Пусть G 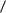V , 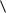- некоторый граф. Подмножество вершин V V

называется множеством внешней устойчивости, если

1) V V V

2) V V V V V

Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа G . Для того,

чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.

Дискретная математика: теория графов

Множества внешней устойчивости:

v1 v2 v3 v6 v1 v2 v3 v5 v1 v2 v3 v4

v3 v4 v5 v6 v2 v4 v5 v6 v1 v4 v5 v6

v1 v2 v3 v4v5v6 v1v2v3 v4 v5 v6

v1v2v3 v4v5v6 v1v4 v1v5 v1v6 v2v4 v2v5 v2v6 v3v4 v3v5 v3v6

v1,v2 ,v3 ; v4 ,v5 ,v6 ; v1,v4 ; v1,v5 ; v1,v6 ; v2 ,v4 ; v2 ,v5 ; v2 ,v6 ;

v3 ,v4 ; v3 ,v5 ; v3 ,v6

G 2

Внешняя устойчивость орграфа

V есть множество положительной внешней устойчивости

орграфа G 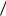V , 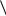, если

1)V V V

2)V V V V V .

Число положительной внешней устойчивости орграфа – мощность минимального множества положительной внешней устойчивости G .

V есть множество отрицательной внешней устойчивости

орграфа G 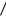V , 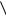, если

1)V V V

2)V V V V V .

Число отрицательной внешней устойчивости орграфа – мощность минимального множества отрицательной внешней устойчивости G .

Поиск множеств положительной (отрицательной) внешней устойчивости орграфа производится по модифицированной матрице смежности (модификация заключается в добавлении единичной главной диагонали) с помощью покрытия. При этом покрытия столбцов строками порождают все множества

Дискретная математика: теория графов

положительной внешней устойчивости, а покрытия всех строк столбцами порождают все множества отрицательной внешней устойчивости.

Пример

Множества отрицательной внешней устойчивости:

x1 x2 x4 x6 x2 x3 x3 x6 x3 x4 x5 x5 x5 x6x1 x2 x4 x6 x3 x2 x6 x5

x1x3 x5 x2 x3 x5 x3 x4 x5 x3 x5 x6 x1x2 x5 x6 x2 x5 x6 x2 x4 x5 x6

G 3

Внутренняя устойчивость графа

Подмножество вершин графа называется внутренне устойчивым, если они попарно несмежны между собой. Внутренне устойчивое множество вершин называется пустым подграфом, если при добавлении хотя бы одной вершины свойство внутренней устойчивости пропадает.

Дискретная математика: теория графов

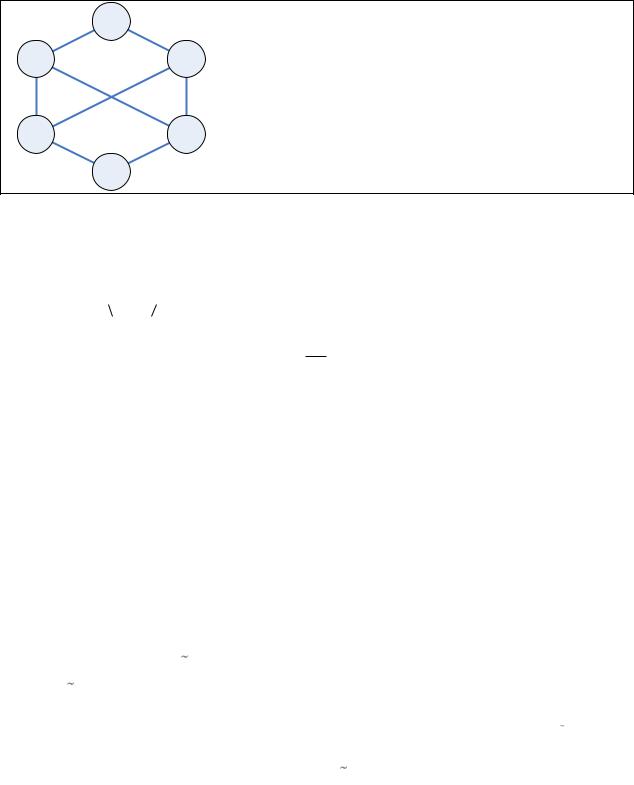
Пример

Мощность максимального пустого подграфа называется числом внутренней устойчивости графа 0 G .

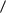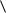Пусть G V , - некоторый граф, v V - некоторая вершина,G v - окрестность вершины v . Неокрестность (коокрестность) вершины v графа G обозначим Gv - подграф графа G , порожденный V v G v .

Теорема

Пустой подграф, содержащий вершину v содержит по крайней мере одну вершину из коокрестности вершины v .

Алгоритм нахождения пустых подграфов

Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф G .

Итерационный шаг: на i -ом ярусе есть вершина, которой сопоставлен граф G .

а) Из G выбирается любая вершина v и выносится на i 1 ярус. б) На i 1 ярус выносятся все вершины, которые входят в G v . в) Каждая из вершин i 1 яруса взвешивается соответствующим графом – коокрестностью от графа G .

Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф.

Замечание В пункте а) желательно выбирать ту вершину, которая имеет

минимальную степень.