Терехин. Учебное пособие

•с изменением направления движения момент сопротивления ме няет знак на противоположный. Это положение находит подтвер

ждение при реверсе (текущее время 3 с и больше). В момент ревер са двигатель развивает момент Те = –34,17 Н.м, частота вращения начинает уменьшаться и момент сопротивления остаётся положи тельным, так как частота вращения положительна. Суммарный

момент на валу двигателя определяется как (–Те – ТL) и имеет мак симальное значение, что определяет значительно бо' льшую интен сивность торможения до нулевой частоты, чем интенсивность пу ска на отрицательную, когда реактивный момент меняет знак, а суммарный момент на валу двигателя составляет меньшее значе ние (–Те + ТL). Данные рассуждения подтверждаются при рассмо трении диаграммы частоты вращения после 3 с.

На рис. 1.30 представлены статические механические характери стики, построенные в процессах пуска и реверса двигателя. Участок 1–2–3 нелинейный, так как меняется ток возбуждения. Максимальное значение момента на этом участке составляет значение 12,29 Н.м. При пуске с установившимся значением тока возбуждения пусковой момент достигает примерно 20 Н.м. Поэтому включать в работу двигатель наи более целесообразно с номинальным током возбуждения для достиже ния высокого быстродействия и снижения потерь при пуске. При до стижении током возбуждения установившегося значения механическая характеристика двигателя принимает классический вид – прямая с на

31

клоном, определяемым полным сопротивлением цепи обмотки якоря (участки 4–5 противоточного торможения и 5–6 двигательного режима «назад»).

Одновременное воздействие реактивного и активного моментов нагрузки TL = 3 Н.м, Ta = 5 Н.м произведём на модели (рис. 1.31), ана логичной ранее использовавшейся. Отличие модели, приведённой в файле Fig 1_31, состоит в изменении порядка представления осцилло грамм на диаграмме: частота вращения, момент двигателя, ток возбуж дения и ток обмотки якоря.

Рис. 1.31. Модель электропривода постоянного тока (Fig 1_31)

Результаты моделирования представлены на рис. 1.32. Так как ак тивный момент больше реактивного, то следует ожидать в начале пуска появление отрицательной частоты вращения (рис. 1.33). Это вызвано нулевым начальным значением момента двигателя. Активный момент нагрузки Ta = 5 Н.м при нулевой частоте вращения двигателя определя ет начало движения «назад». Когда появилась отрицательная частота вращения, появился отрицательный реактивный момент TL = –3 Н.м. При текущем значении момента двигателя в 2 Н.м и более, прекращает ся рост отрицательной частоты вращения и начинается её повышение до нулевого значения. Далее нулевое значение сохраняется до момента времени, когда текущее значение момента двигателя Tе не превысит суммарное значение Tа + TL = 5 + 3 = 8 Н.м (см. рис. 1.32, осциллограм мы 1 и 2).

32

Рис. 1.33. Начальный фрагмент осциллограммы частоты вращения, приведённой на рис. 1.32

Двигатель разгоняется до частоты вращения 139,5 1/с, развивает положительный момент 8,332 Н.м, который, если представить возмож ность пуска более 3 с, достигнет значения 8 Н.м. Двигатель преодолева ет сумму моментов сопротивления Tа + TL= 5 + 3 = 8 Н.м. Уравнение равновесия моментов для установившегося режима имеет вид:

При пуске «вперёд» момент двигателя Tе – положительный, актив ный момент Tа по условию исследуемой задачи – положительный, знак реактивного момента TL (определяется по знаку частоты вращения) – положительный. Из уравнения равновесия (1.9) следует: Tе = Tа + TL. При положительных знаках моментов сопротивления при работе «впе рёд» двигатель должен преодолевать момент сопротивления 8 Н.м. При

33

работе двигателя «назад» знак активного момента не меняется, а реак тивный меняет знак на отрицательный. Из уравнения равновесия сле дует: Tе = Tа + TL = 5 + (–3) = 2 Н.м. По осциллограмме на рис. 1.31 это значение составило +1,722 Н.м, что означает работу двигателя в режи ме генераторного торможения с частотой вращения –258,6 1/с (см. рис. 1.34, т. 6) большей, чем частота вращения идеального холосто го хода –238 1/с (т. 5 на рис. 1.34).

Рис. 1.34. Механические характеристики двигателя

при пуске и реверсе с моментами нагрузки TL = 3 Н.м, Ta = 5 Н.м

Особый интерес представляет случай равенства активного и реак тивного моментов сопротивления (TL = 5 Н.м, Ta = 5 Н.м) с позиции выполнения этого частного режима моделью двигателя постоянного тока. Откроем модель Fig 1_31, занесём выбранные значения моментов сопротивления и выполним моделирование.

Прежде чем приступить к анализу полученных результатов, выска жем ряд соображений. Если предположить, что в начале пуска (ω = 0) и реактивный момент TL = 0, то за счет активного момента Ta, при нулевом значении Tе, суммарный момент на валу двигателя Tе – Ta < 0 и двигатель начинает движение «назад». Однако если бы это произошло, то появил ся бы реактивный момент отрицательного значения TL = –5 Н.м, а сум марный момент на валу двигателя составил бы значение Tе – Tа – TL = = Те – 5 – (–5) = Tе ≥ 0 Н.м. При пуске момент двигателя Tе увеличива

34

ется от нулевого значения. Следует предположить, что двигатель дол жен начать движение «вперёд». В этом случае знак реактивного момен та станет положительным и составит TL = 5 Н.м. Суммарный момент сопротивления Ta + TL = 5 + 5 = 10 Н.м. Это означает, что движение «назад» невозможно, а движение «вперёд» начнётся тогда, когда теку щее значение момента двигателя превысит суммарное сопротивление при движении «вперёд». Модель успешно справилась с этой задачей, что видно по осциллограммам, полученным в ходе моделирования дан ной ситуации (рис. 1.35).

Для исключения толкования, что двигатель сделал попытку дви жения «назад», приведён увеличенный фрагмент начального участка осциллограммы частоты вращения (рис. 1.36), где появление отрица тельной и положительной частоты вращения не зафиксировано во вре мени, пока момент двигателя был меньше 10 Н.м.

Двигатель разогнался «вперёд» до частоты вращения 116 1/с, прео долевая суммарный момент сопротивления, равный 10 Н.м (по осцил лограмме на рис. 1.35 – +10,36 Н.м).

35

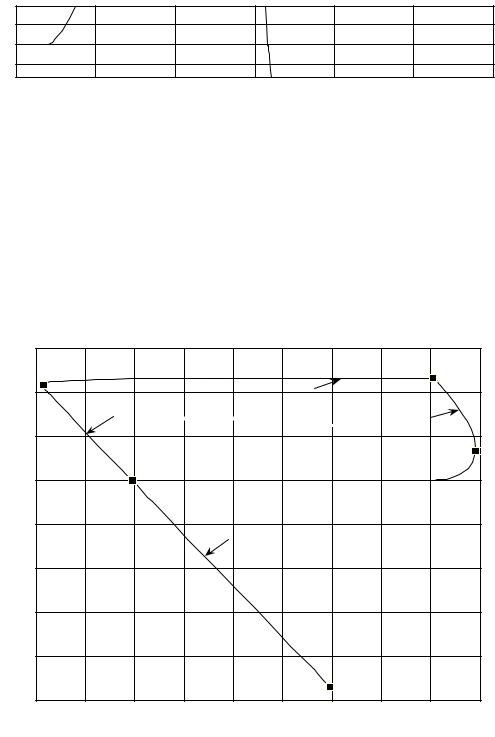
Рис. 1.36. Увеличенный фрагмент осциллограммы частоты вращения на начальном участке пуска

При реверсе «назад» двигатель интенсивно затормозился до нуле вой частоты, так как суммарный момент составлял 10 Н.м (см. рис. 1.35). Пуск на отрицательную частоту вращения («назад») осу ществляется при суммарном моменте сопротивления, равным нулево му значению, т. е. в холостую (активный момент уравновешивается ре активным моментом сопротивления, изменившим знак вместе с часто той вращения). Частота вращения достигает примерно частоты холо стого хода –235,1 1/с, а момент двигателя составляет –0,1982 Н.м.

36

зависимости от параметров нагрузки максимальный момент при пуске «вперёд» составил 14,49 Н.м.

Таким образом, исследования разработанной виртуальной модели двигателя постоянного тока в Simulink подтвердили её работоспособ ность с любым сочетанием активных и реактивных моментов сопро тивления. Использование данной модели двигателя позволяет модели ровать всевозможные режимы работы с любым видом нагрузки.

Читателю предлагается проверить работу двигателя по схеме на рис. 1.31 с реактивным моментом сопротивления 25 Н.м и активным моментом сопротивления +25 Н.м.

1.2.Машина переменного тока (асинхронная)

1.2.1.Математическое описание обобщенной асинхронной машины

Токи и напряжения фаз статора (ротора тоже) асинхронного дви гателя можно представить в виде пространственного вектора [4], что приводит к сокращению числа и упрощению структуры уравнений, описывающих рабочие процессы асинхронного двигателя.

В общем случае на трёхфазной обмотке статора действует трёхфаз ная система напряжений:

Если ось А координатной системы А, В, С совместить с веществен ной осью комплексной плоскости, расположенной перпендикулярно валу машины, то пространственный (обобщенный) вектор напряжения на обмотках статора асинхронного двигателя определяется уравнением:

где U6A, U6B, U6C – мгновенные значения фазных напряжений (1.10); a – оператор поворота:

37

a = e j 2π /3 = −1/ 2 + j 3 / 2;

Подставим в формулу для пространственного вектора (1.11) выра жения (1.10) и (1.12):

При преобразовании полученного выражения использованы сле дующие соотношения:

sin(ωt ± 23π ) =sinωt cos( 23π ) ±cos ωtsin( 23π),

Приведем полученное комплексное выражение к стандартной тригонометрической форме, заменив sinωt = cos(π/2 – ωt) и cosωt =

что указывает на возникновение постоянной по амплитуде Um простран ственной волны напряжения, вращающейся в положительном направлении с частотой ω. Начальное положение пространственного вектора при t = 0 со ответствует углу (–π/2), что позволяет получить его проекции при вращении на оси А, В, С, изменяющиеся в соответствии с формулами (1.10).

На рис. 1.38 представлена геометрическая интерпретация про странственного вектора напряжения – это вектор на комплексной пло

скости с модулем (длиной) U , вращающийся с угловой скоростью ω в

m 6

положительном направлении. Проекции вектора US на фазные оси А, В, С определяют мгновенные напряжения в фазах. Аналогично простран

38

ственными векторами можно представить все напряжения, токи и по токосцепления, входящие в уравнения, описывающие работу асин хронного двигателя.

( Im)

ȼ

Ⱥ

При построении реальных систем электропривода переменного тока, как асинхронных, так и синхронных, практически всегда в систе му управления включают преобразователи фаз 3/2 и 2/3 [2].

Первый (3/2) – преобразовывает фазные напряжения трёхфазной системы в напряжения двухфазной системы в координатах α, β. Отме тим, что как трёхосная координатная система А, В, С, так и двухосная α, β являются неподвижными системами. Пространственный вектор изображает результат совместного действия трёхфазной системы токов любой эквивалентной m фазной и, в частности, двухфазной системы. Переход к двухфазной системе в математическом отношении эквива лентен рассмотрению пространственного вектора в новой прямоуголь ной системе координат α, β. Физический смысл такого преобразования координат состоит в замене реальной трёхфазной машины эквивалент ной двухфазной моделью, характеризующейся тем же значением про странственного вектора. Такая замена переменных широко использует ся при математическом исследовании электрических машин с целью упрощения систем дифференциальных уравнений электрического рав новесия статорных и роторных цепей.

Преобразователь (3/2) осуществляет преобразование трёхфазных напряжений UA, UB, UC (1.10) в двухфазные Uα, Uβ, в соответствии с вы ражениями (1.11) и (1.12):

39

После преобразования уравнения (1.18) получим

Uα = 2[UA −(UB +UC ) / 2] / 3,

Рис. 1.39. Преобразование координат:

а) условное графическое обозначение преобразователя; б) координаты

При этом следует иметь в виду, что фазная ось α прямоугольной (двухфазной) системы совмещена с фазной осью А трёхфазной системы (рис. 1.39, б).

На рис. 1.40 показана модель преобразователя (3/2) в Simulink (Matlab) [2].

Рис. 1.40. Модель преобразователя (3/2) (Fig 1_40)

На рис. 1.41 показан результат преобразования трёхфазного на пряжения в двухфазное.

Амплитуда напряжения принята Um = 1 В, частота ω = 314 рад/с (f = 50 Гц). Пространственный вектор напряжения в координатах α, β описывается выражением (1.15), полученным для трёхфазной системы напряжений U6 = Um(sinωt – jcosωt). Из уравнения (1.15) следует, что в двухфазной системе напряжения вычисляются как Uα = Umsinωt и

40