Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Теория функций комплексного переменного

Файл:

Михайлов ТФКП практикум2013

.pdf

Скачиваний:

1697

Добавлен:

05.06.2015

Размер:

4 Мб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 257 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Пример 5.1. Определить: 1) на какую область отображает функция w = z2 второй

квадрант плоскости z ( x < 0, y > 0)							(рис. 5.1);
2) на		z	какую область отображает				функция
w =				полукруг	z	<1 , Im z > 0 (рис. 5.2);

	z	−1

3) [3], № 2.107 (9).
Решение.
1)			w = z2 = (x +iy)2 = x2 − y2 + 2ixy (см.

рис. 5 .1). Пусть w = u + iυ. Тогда u = x2 − y2 ; υ = 2 xy . По принципу соответствия границ верхняя мнимая полуось {x = 0; 0 ≤ y ≤ +∞} отображается следующим образом: u = −y2 ; υ = 0 , то есть в отрицательную действительную полуось {−∞ < u ≤ 0; υ = 0} .

Отрицательная действительная полуось {−∞ < x ≤ 0; y = 0} отображается так: u = x2 ,

υ = 0 , то есть переходит в действительную положительную полуось. Так как направление обхода при конформном отображении сохраняется, то второй квадрант отображается в нижнюю полуплоскость (рис. 5.3) (можно этот факт установить и с помощью какойлибо пробной внутренней точки, взятой из отображаемой области, например:

Рис. 5.1

Рис. 5.2

Рис. 5.3

z= −1+i → w = (−1+i)2 = −2i .

2)Отрезок действительной оси −1 ≤ x ≤1 отображается в дейст-

вительную полуось	−∞ < u ≤	1	(так	как−1 →	1	, 0 → 0 ,	1 → −∞ ).
		2			2

Полуокружность z = eiφ (0 ≤ φ ≤ π) преобразуется следующим образом:

w =

eiφ

eiφ(e−iφ −1)

1−eiφ

1 −eiφ

iφ

−1)(e

−iφ

−1)

−e

iφ

−e

−iφ

2(1−cosφ)

−1

1−cos ϕ−i sin φ

−

isin φ

2(1−cos φ)

i2 sin

= =

−

2 cos

−

(0 ≤ φ ≤ π) u =

4 cos

2 φ

−∞ < υ ≤ 0 .

Таким образом, полукруг отображается

во

внутренность

прямого

угла

(рис. 5.4).

u <

; υ< 0

На какую область функция Жуков-

ского

w =

отображает

область

Рис. 5.4

>1 ,

Im z > 0 (рис.

5.5)?

Часть

действи-

тельной оси

x (−∞;−1] [1; +∞)

преобра-

зуется следующим образом:

;

u =

υ = 0 .

x +

Когда х меняется от –∞ до –1,

перемен-

ная

также

меняется от –∞ до –1. Одина-

Рис. 5.5

ково они меняются и когда x [1;+∞). Ок-

ружность

z = eiφ

отображается

так:

w =

(eiφ

+e−iφ)= cosφ, то есть переходит

отрезок

действительной

оси

−1 ≤ u ≤1 .

Таким образом, данная область отобража-

ется

верхнюю

полуплоскость

Im w > 0

Рис. 5.6

(рис. 5.6).

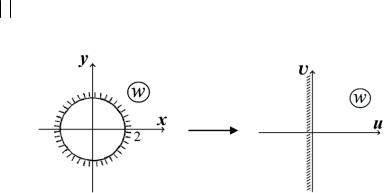
Пример 5.2 ([3], № 2.30). Найти функцию, отображающую круг z < 2 на полуплоскость Re w > 0 так, чтобы w(0) =1 , arg w′(0) = π2

(рис. 5.7 и 5.8).

Рис. 5.7

Рис. 5.8

Решение. Будем искать решение в виде дробно-линейной

функции w = λ

z −α

(так как именно она может перевести окруж-

z −β

ность в прямую). Используем условие

z −α

w(0) =1 1 = λ α

λ =

β ;

w =

z −β

Симметричная точке z = 0

относительно границы (т.е.

окруж-

ности) точка z =∞.

Поэтому симметричная точке

w =1

относи-

тельно образа этой границы (то есть прямой u = 0 ) точка

w = −1 .

Следовательно,

w(∞) = −1 = lim β

z −α

α = −β.

z→∞ α

z −β

Таким образом, w = −

z −α

z +α

2α

; w′(0) = − 2 .

Используем

условие

w′(0) =

: w′(z)

= −

+α)2

Если α =

eiφ0 , то w′(0) = −2

e−iφ0

и arg w′(0) = π−φ0

π−φ0

φ0

α =

i w(z) = −

z −i

z +i

Для нахождения α используем условие: граница переходит в границу. Следовательно, окружность z = 2 eiφ переходит в прямую

u = 0 . Итак,

(2eiφ −i

)(2e−iφ −i

)

u +iυ = −

2eiφ −i

= (2eiφ +i

)(2e−iφ −i

)

2eiφ +i

= −

4 −

−i

2e−iφ

−i

2eiφ

= −

4 −

2 −2i

2 cos φ

2eiφ +i

u = −

4 −

= 0

= 2 .

2eiφ +i

Ответ: w = − zz +−22ii .

Пример 5.3 ([3], № 2.31). Отобразить круг z −4i < 2 на полу-

плоскость υ > u так, чтобы центр круга перешел в точку −4 , а точка окружности 2i – в начало координат (рис. 5.9 и 5.10).

Рис. 5.9	Рис. 5.10
Решение. Используем дробно-линейную функцию w = λ		z −α		.

			z −β
Так как точка 2i	переходит в начало координат, то w = λ		z −2i		.

			z −β

Центр круга точка z = 4i переходит в точку −4 . Следовательно,

−4 = λ 44ii−−2βi ; −2(4i −β) = 2iλ ; −8i +2β = 2 iλ ,

λ = −4 −iβ w = −(4 +iβ) zz−−2βi .

Для центра круга симметричной относительно окружности будет точка z =∞. Она переходит в точку w0 = −4i , симметричную

точке –4 относитель но образа окруж ности, то есть относительно прямо й υ = u .

w(∞) = −4i = lim −(4 +iβ)		z − 2i		= −4 −iβ β = 4 + 4i
		z −β
	z→∞
	w = −4i		z −2i		.
Пр имер 5.4			z −4 −4i

	([3], № 2.99). Отобразить на верхн юю полуплос-
кость Im w > 0	полуплоскость	Im z > 0 с разрезом по отрезку
[0,ih], h > 0 (рис. 5.1 1 и 5.12).

Рис. 5.11 Рис. 5.12

Делаем поэтапно: 1) w = z2		(рис. 5.13);	2)	w		= w + h2	(рис.
	1				2	1
5.14); 3) w = w	(рис. 5.15). Получаем ответ		w =		z2 + h2
2

Рис. 5.13

Рис. 5.14

Рис. 5.15


Пр имер 5.5 ([3], № 2.101).				Отобразить на верхнюю полуплос-
кость	Im w > 0 полуплоскость			Im z > 0 с разрезом по дуге окруж-
ности		z	=1 от точки z =1 до точки z = eiα , где 0 < α < π (рис. 5.16
ности		z

и 5.17 ).

Рис. 5.16 Рис. 5.17

Решение. Делаем

поэтапно.

Сначала

применим дробно-

линейную функциюw

z −1

, получим ре-

z +1

зультат, показанный на рис. 5.18.

Так как при этом преобразовании дейст-

вительная ось переходит в действительную,

верхняя полуплоскость переходит в верх-

нюю полуплоскость, единичная окружность

=1 переходит в мнимую ось,

точка

z =1

Рис. 5.18

переходит в точку w = 0 , точка z =eiα

переходит в точку

e −1

(

iα

)(

−iα

)

−e + e

2i sin α

iα

−

1 e

−iα

iα

w = eiα +1 = (eiα +1)(e−iα +1)= 2 + eiα + e−iα = 2 + 2 cosα =

αα

=i2sin 2 cos 2 = i tg α . 2 cos2 α2 2

Далее: w = w2		(рис. 5.19),	w = w + tg2 α			(рис. 5.20), w = w
2	1		3	2	2				3
					2
				z −1	2		2	α
(рис. 5.21). Окончательный ответ:					+ tg			2	.
(рис. 5.21). Окончательный ответ:					+ tg				.
				z +1


Рис. 5.19	Рис. 5.20	Рис. 5.21
Пр имер 5.6 ([3],	№ 2.118). Отобразить единичный круг		z	< 1 с
Пр имер 5.6 ([3],	№ 2.118). Отобразить единичный круг		z	< 1 с

выки нутым отрезком (1−h)eiα,eiα (рис. 5.22) на единичный круг

|w| < 1 .

	Рис. 5.22						Рис. 5.23
Решение. Сначала получим единичный
круг	разрезом по действительной оси [0;1]
(рис. 5.23):							(1 −h)eiα − z
		w = e−iα					(1 −h)eiα − z
		w = e−iα
		1					z (1 −h)e−iα −1
							z (1 −h)e−iα −1
(см. таблицу отображений).
Далее:
w2	=	w1 (рис. 5.24),
w3	= 1	w2 +		1	(рис. 5.25),
w3	= 1	w2 +			(рис. 5.25),
	2			w2
w	= w = −		w3 +i			(рис. 5.26).
w	= w = −					(рис. 5.26).
4			w3 −i
			w3 −i
							67

Рис. 5.24

Рис. 5.25

Рис. 5.26

Пр имер 5.7 ([3],	№ 2.166). Отобразить на верхн юю полуплос-
кость полуполосу	0 < x < π, y > 0 с разрезом вдоль отрезка

x = π2 , 0 ≤ y ≤ h (рис. 5.27).

Рис. 5.27 Рис. 5.28 Рис. 5.29

Решение. Сначала		w1 = −cos z (рис. 5.28), далее по таблице

изображений w =	w 2	+sh2 h (рис. 5.29).
2	1

Рекомендуемый перечень задач для решения в ау дитории:

5.1 (2, 3); 5.2 ([3], № 2.30); 5.4; 5. 5; [3] № 2.164; 5.7 ([3], № 2.166).

Резерв:

[3], № 2.97, № 2.117; 5.6 ([3], № 2. 118).

Для самостоятельной работы дома:

5.1 (1); [3], № 2.100; 5.3 ([3], № 2. 31); [3] № 2.107 (8), № 2.167.

6. ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ

Пусть на комплексной плоскости z задана кривая γ, соединяющая точки А и В, и на этой кривой задана функция w = f (z) . Про-

изведем разбиение кривой точками A = z0 , z1, z2 ,… , zn = B . Обозначим разность zi+1 − zi = zi (i = 0,1,…,n −1) . На кривой между соседними точками разбиения возьмем произвольно точки ξi и

составим интегральную сумму

σ = ∑ f (ξi ) zi .

i=1

Увеличивая число точек разбиения n → ∞ так, чтобы характе-

ристика разбиения λ = max	zi	→ 0 , получим предел инте-
ристика разбиения λ = max	zi	→ 0 , получим предел инте-
i=0,1...,n−1
i=0,1...,n−1

гральных сумм, который, если он существует, называется интегралом по комплексной переменной вдоль кривой γ: lim σ = ∫ f (z)dz .

λ→0

n→∞ γ

Этот интеграл сводится к криволинейному интегралу второго рода от действительных функций двух действительных переменных х и

у, где	z = x +iy ,	вдоль кривой	γ. Действительно, если
w = f ( z) = u (x, y) +iυ( x, y) , а dz = dx +idy , то
∫ f (z)dz = ∫(u +iυ)(dx +idy) = ∫udx −υdy +i∫υdx +udy .
γ	γ	γ	γ

Если кривая γ замкнута, без самопересечений (будем называть ее контуром), а функция f (z) аналитическая внутри γ и непрерыв-

ная в области с границей, то функции и и υ непрерывны вместе со своими частными производными первого порядка, при этом справедлива формула Грина

		∂Q	−	∂P
∫ Pdx +Qdy = ∫∫		∂x	−	dxdy
γ	D	∂x		∂y

(D – область с границей γ). В нашем случае:


		−	∂υ	−		∂u			,
∫udx −υdy = ∫∫			∂x			∂y		dxdy
γ	D
∫υdx +udy = ∫∫ ∂u −					∂υ		dxdy .
γ	D ∂x				∂y

Оба двойных интеграла по области D равны нулю в силу условий Коши–Римана. Таким образом, если контур γ ограничивает об-

ласть аналитичности функции f (z) , то ∫ f (z)dz = 0 (теорема Ко-

ши). Отметим, что теорема Коши справедлива и для многосвязной области, где γ – совокупная граница всей многосвязной области. Из теоремы Коши следует интегральная формула Коши:

	1 f (ζ)dζ
f (z) =		∫γ		,
	2πi		ζ− z

где контур γ охватывает область аналитичности функции f (z) , а точка z находится внутри него, ζ γ. Действительно, рассматривая двусвязную область, ограниченную извне контуром γ, а изнутри окружностью ζ− z =ε с центром в точке z, по теореме Коши полу-

чим:

f (ζ)dζ

∫

−

∫

= 0

ζ− z

ζ−z

=ε

или

f (ζ)dζ

∫

= ∫

γ ζ− z

ζ−z

=ε

ζ− z

Обозначим ζ− z = εeiφ , dζ = iεeiφdφ. Интеграл справа будет равен

2π	f (z +εeiφ)iεeiφdφ		2π	iφ			iφ*
∫			= i ∫ f (z +εe		)dφ = i f (z +εe			)2π
∫	εe	iφ	= i ∫ f (z +εe		)dφ = i f (z +εe			)2π
0	εe		0
(по теореме о среднем для интеграла).						lim f (z +εeiφ ) = f (z) , от-
Ввиду непрерывности функции f (z) ,						lim f (z +εeiφ ) = f (z) , от-
						ε→0

куда и получаем формулу Коши, которая также справедлива для многосвязной области.

<<< < Предыдущая 1 2 3 4 5 67 / 257 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>