Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Теория функций комплексного переменного

Файл:

Михайлов ТФКП практикум2013

.pdf

Скачиваний:

1697

Добавлен:

05.06.2015

Размер:

4 Мб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2522 23 24 25 > Следующая >>>

Интегралы по малой полуокружности при ρ → 0 и по большой полуокружности при R → ∞ обращаются в 0 (показывается, как в предыдущих примерах). Получаем

∞

−πe

−i

3π

J −i J + π

∫0

−3ln a +i

x(x

+ a

)

Приравниваем мнимые части слева и справа:

−J =

−π

[cos

3π −sin

(2 −3ln a)] ;

4a3

3π

J =

−2 +3ln a

ln a −1

Пример 13.20 ([3], № 4.202). Вычислить интеграл ∞∫sin axdx.

0 shx

Решение. Рассмотрим интеграл ∫eaizdz									, где контур С указан на
					C shz
рис. 13.13. Внутри контура одна особая
точка z = πi – полюс первого порядка.
Вычислим вычет в ней по формуле						φ		, где

						ψ′
φ(z) = eiaz , ψ(z) = shz :
res[ f (z), πi] =	e−aπ	=	e−aπ	= −e	−aπ		.
	chπi		cos π						Рис. 13.13

Интеграл равен

2πi res[ f (z), πi] = −2πie−aπ .

Вычислим интегралы по составным частям контура С. Интеграл по малой полуокружности радиуса ρ с центром в начале координат

∫eaiz dz = −πires[ f (z),0] = −πi Cρ shz

(см. вычисление интегралов с особенностями на действительной оси). Аналогично вычисляется интеграл по малой полуокружности с центром в точке 2πi (также полюс первого порядка).

211

∫	eaiz dz = −πires[ f (z), 2πi] = −πie−2πa .
Cρ′	shz
Cρ′
Интеграл по действительной оси
	−ρ	eiaxdx	+ ∫α eiaxdx			+∞∫	eiaxdx .
	∫	eiaxdx	+ ∫α eiaxdx		→	+∞∫	eiaxdx .
	−α	shx	ρ	shx	ρ→0	−∞		shx
	−α		ρ		α→∞	−∞
Интеграл по горизонтальной прямой						z = x + 2πi в пределе при
ρ → 0 , α → ∞ равен
	−∞∫	eia( x+2πi)dx		= −e−2πa +∞∫				eiax	dx .
	−∞∫			= −e−2πa +∞∫					dx .
	+∞ sh(x + 2πi)					−∞ shx

Оценим интегралы по вертикальным отрезкам: z = ±α+iy , 0 ≤ y ≤ 2π ,

2∫π eia(α+iy)idy	≤	2∫π	e−aydy	→ 0
0 sh(α+iy)		0	sh(α+iy)
0 sh(α+iy)		0	sh(α+iy)

при α → ∞ .

Аналогично, по левому вертикальному отрезку интеграл стремится к нулю. В результате имеем равенство

+∞∫	eiaxdx	−e−2πa +∞∫	eiaxdx	−πi −πie−2πa = −2πie−πa .
−∞	shx	−∞	shx

Приравняем мнимые части слева и справа:

(1−e−2πa ) ∞∫

sin ax dx −π−πe−2πa = −2πe−aπ

−∞

shx

+∞ sin ax dx

−2πe−aπ + πe−2aπ + π

π(1−e−aπ)2

∫

−2aπ

shx

1−e

−e

−aπ

)(1+e

−aπ

)

−∞

π(1−e−aπ)

aπ

∞ sin ax dx

aπ

1+e

−aπ

= π th

∫

shx

212

Рекомендуемый перечень задач для решения в аудитории:

13.1 ([3], № 4.165); 13.2 ([3], № 4.166); 13.5 ([3], № 4.170); 13.8 ([3], № 4.177); 13.12 ([3], № 4.181); 13.17 ([3], № 4.190); 13.19 ([3], № 4.192).

Резерв:

13.4 ([3], № 4.168); 13.7 ([3], № 4.176); 13.13 ([3], № 4.183), 13.14 ([3], № 4.184); 13.15 ([3], № 4.185); 13.20 ([3], № 4.202).

Для самостоятельной работы дома:

13.3 ([3], № 4.167); 13.6 ([3], № 4.172); 13.9 ([3], № 4.178), 13.11 ([3], № 4.180); 13.18 ([3], № 4.191).

На усмотрение преподавателя:

13.10 ([3], № 4.179); 13.16 ([3], № 4.186).

213

14. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

Рассмотрим интегральное преобразование Лапласа, его свойства и применения, то есть раздел математики, который обычно называют операционным исчислением.

Интеграл Лапласа имеет вид

∞

F( p) = ∫e−pt f (t)dt ,

где функция действительного переменного f (t) называется оригиналом, а F ( p) – функция комплексного переменного р называется её изображением по Лапласу. Соответствие между f (t) и F ( p) будем изображать знаком . Функциями, которые могут

быть оригиналом, являются не только действительные, но и комплекснозначные функции f (t) , отвечающие следующим требова-

ниям:

1)f (t) ≡ 0 при t < 0 ;

2)на каждом конечном промежутке оси t f (t) имеет не более

конечного числа разрывов первого рода;

3) f (t) при t → +∞ имеет ограниченную степень роста, что значит: f (t) ≤ Meat , где М и а – некоторые постоянные. При этом

наименьшее из всех а называется показателем степени роста функции f (t) . Можно показать, что функция F ( p) – аналитиче-

ская в полуплоскости Re p > a , где а – показатель степени роста функции f (t) .

Свойства изображений

1. Свойство линейности:

∑ αi fi (t) αi Fi ( p) (αi = const, i =1, 2...n) .

i=1

2.f (αt) α1 F ( αp ) , α= const > 0 .

3.Теорема запаздывания:

214

0, τ > t,

f (t)

e− pτF( p) .

(t) =

f (t −τ), τ≤t,

(n−1)τ

(n)

f (o)

(o)

(t) p

{F( p) −

−... −

} ,

5. ∫0

f (τ)dτ

F( p) .

6. Изображение свертки:

f1(t −τ) f2 (τ)dτ F1( p) F2 ( p) .

∫0

f1 (τ) f2 (t −τ)dτ =

∫0

7.F(n) ( p) (−1)n tn f (t) .

8.∞∫F( p)dp f t(t) .

9.Теорема смещения: F ( p + λ) e−λt f (t) .

Изображения некоторых функций

1. 1 1p ; Re p > 0 . Под единицей понимается единичная функ-

0,если t < 0,

ция Хевисайда σ0 (t) : σ0 (t) =

1,если t ≥ 0.

Все функции в дальнейшем будем считать умноженными на эту единичную функцию.

2.tv Γ(pvv++11) , v >−1, Re p > 0 ; Γ(v) – гамма-функция.

3.При v = n (n – целое) tn pnn!+1 , Re p > 0 .

4.eαt p 1−α , Re p > Re α .

5.sin ωt p2 ω+ω2 , Re p > Im ω ;

215

cos ωt

, Re p >

Im ω

p2 +ω2

shλt

Re p > Re λ .

p2 −λ2

ch λt

, Re p > Re λ .

p2 −λ2

Изображения других элементарных функций могут быть получены с помощью свойств из соответствующей таблицы.

Перейдем к определению оригинала по изображению, а также обратному преобразованию Лапласа (преобразованию Меллина).

Если F(p), где p = x + iy – аналитическая в области Rep > a функция, равномерно относительно arg p стремящаяся к нулю при

p	→∞ , и для всех Re p > a сходится интеграл	x+∫i∞	F( p)	dy < M ,

		x−i∞

x > a , то F ( p) при Re p > a является изображением функции f (t), которая определяется выражением

f (t) =	1	x+∫i∞ept F( p)dp.

	2πi x−i∞

Последний интеграл может вычисляться в комплексной плоскости p с помощью вычетов рассмотренными ранее методами. Частный случай: если F ( p) разлагается на бесконечности в ряд Лорана

	∞	cn
вида	F ( p) = ∑	cn	, то оригиналом этой функции является функ-
вида	F ( p) = ∑	n	, то оригиналом этой функции является функ-
	n=1	p
			∞	t	n
ция	f (t) = 0 , если t < 0 , и f (t) = ∑cn+1			t		, если t ≥ 0 .
ция	f (t) = 0 , если t < 0 , и f (t) = ∑cn+1			n!		, если t ≥ 0 .
			n=0	n!

Пример 14.1 ([4], № 3). Пользуясь теоремой подобия и таблицей

изображений, найти изображения	следующих функций: 1) eat ;
2) e−at ; 3) shat ; 4) chat ; 5) sin at ;	6) cos at ; 7) cos2 t ; 8) sin	t	.

		a

Решение. 1) Считая известным изображение et p1−1 , по тео-

реме подобия ( f (αt)	1	p
	α		α
		F		), получим

216

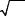
eat	1		1	=	1	.
	a	a
			−1		p −a
		p

3) sht = et

−e−t

sht

и по теореме подобия

1−1

shat

p2 − a2

−1

eit −e−it

5) sin t =

−

sin at

p −i

p +i

p2 +1

+a2

1 + cos 2t

p2 +2

7) cos

p2 +4

p( p2 +4)

Пример 14.2 ([4], № 5). Пользуясь теоремой смещения, найти

изображения следующих функций:

eax sin bx ;

2) chax cos ax ;

3) 1 (chax sin ax +shax cos ax) ;

1 shax sin ax ;

5) e−4 x sin 3x cos 2x ;

6) shx cos 2x cos 3x ;

e−ax

;

e( x+1)( 2−x) .

πx

Решение.

1) eax sin bx

(непосредственно по точке смещения);

( p

−a)2 +b2

1 (ch ax sin ax +sh ax cos ax) ;

chax·sinax =

eax +e−ax

sinax

2 [

] =

( p −a)2 + a2

( p + a)2 + a2

217

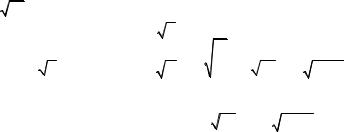
a p2 + 2ap + 2a2 + p2 −2ap + 2a2

2 p2 + 4a2

= 2

( p2 −2ap + 2a2 )(· p2 + 2ap + 2a2 )

( p2 + 2a2 )2 −4a2 p2

a( p2 + 2a2 )

p4 +

4a4

Аналогично:

eax −e−ax

p −a

p + a

shax·cosax =

cosax

2 [

−

] =

( p −a)2 + a2

( p + a)2 + a2

( p2 + 2ap + 2a2 )·( p −a)− ( p2 −2ap + 2a2 )·( p + a)

= 2

( p2 −2ap + 2a2 )(· p2 + 2ap + 2a2 )

= 1

2ap2 −4a3

= a( p2 −2a2 ) .

( p2 + 2a2 )2 −4a2 p2

p4 + 4a4

И, следовательно,

1 (chax·sinax +shax·cosax)

a( p2 +

2a2 )

a( p2

−2a2 )

ap2

2( p4 +

4a4 )

2( p4

+ 4a4 )

+ 4a4

e−4 x sin3x cos2x; используя

формулу

тригонометрии

sin3x·cos2x = 1·(sin5x +sinx),

получим

1 e−4 x (sin5x +sinx)

e−4 x sin3x cos2x =

[

] =

( p + 4)2 + 25

e−ax

;

воспользуемся таблицей изображений:

πx

Γ(1)

= 1

= x−2

;

πx

p + a

e−ax·f

(x)

F( p +a)

e−ax

πx

p +a

218

Пример 14.3 ([4], №6). Пользуясь теоремой смещения и теоремой дифференцирования изображения, найти изображения сле-

дующих функций:

xcosbx ;

x2 sin bx ;

3) x shax sin ax ;

4) x chax cos ax ;

xe−

;

6) x2e3 x .

Решение.

1) xcosbx . Так как cosbx

′и F ′( p) −xf (x) ,

то

p2 +b2

−

p2 −b2

xcosax

−ax p

2 +b2

= ( p2 +b2 )2 .

3) x shax sin ax = x e

−e

sin ax

sin ax ( p −a)2 + a2

(по

теореме смещения),

sin ax

−

′

2a( p −a)

( p −a)2 + a2

(( p −a)2 + a2 )2

−ax

sin ax

2a( p −a)

;

(( p −a)2 + a2 )2

x shax sin ax

p −a

p + a

−

( p

−2 pa + 2a

)

( p

+ 2 pa + 2a

)

2a2 (3 p4 −4a4 )

;

( p4 +4a4 )2

−

−x

1 ′

по теореме

5) xe

2 ;

p +1

( p +1)2

подобия:

−

(2 p +1)

2 .

Пример 14.4 ([4], №7). Пользуясь теоремой запаздывания, най-

ти изображения (a > 0, b > 0): 1) ( )·sin(x – a); 2) cos(ax – b); 3) f(ax – b); 4) f(ax + b).

219

Решение.

1) e( x−a) sin (x −a)= σ0 (x −a)e( x−a) sin (x −a)

		b
3) f (ax −b)= f [a (x	− b )]	e− p a	F (	p	).
		a
	a			a

e−ap	1	.
	( p −a)2 +1

Пример 14.5 ([4], № 8). Пользуясь теоремой интегрирования изображения, найти изображения функций:

sinx

; 2)

e−ax·sinkx

;

cosbx −cosax

;

1−e−ax

;

x·ex

sin7x·sin3x

;

e−ax

bx ;

e−ax −ebx

sin

2 x

·sin

;

Решение.

sinx

∞

∫p

dp =

−arctg p = arctg

p2 +1

e−ax·sinkx

∞

p + a ∞

p + a

∫p

dp = arctg

│p

= 2

−arctg

( p + a)2 + k2

= arctg

p + a

cosbx −cosax

cosbx

cosax

∞

pdp

∞

pdp

−

∫p

− ∫p

p2 +b2

p2 + a2

∞

1 ln( p2

+b2 )

−

1 ln( p2 + a2 )

= 1 ln

+ a

= −

1 ln

= ln

+ a

sin7x·sin3x

cos4x −cos10x

+16)−

2 [

2 ln (p

∞

p2 +100

−

2 ln (p

+100)]

4 ln

p2 +16

220

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2522 23 24 25 > Следующая >>>