РГР2_син_токТОЭ

Рисунок 5

исовпадающим по фазе с входным напряжением.

Кусловию резонанса в данном контуре можно прийти изменением частоты или параметров динамических элементов (L,C).

Резонансу в рассматриваемом контуре соответствует векторная диаграмма,

изображенная на рисунке 6.

Рисунок 6

Из диаграммы видно, что при резонансе приложенное напряжение равно падению напряжения на активном сопротивлении цепи: U=UR

21

Напряжения на емкости UC и индуктивности UL равны по величине и противоположны по фазе и поэтому взаимно уравновешиваются. При резонансе в рассматриваемом контуре напряжения на емкости и на индуктивности могут оказаться значительно больше приложенного напряжения. Поэтому резонанс при последовательном соединении называется резонансом напряжений.

Указанные местные перенапряжения возможны при определенном

Перенапряжения в контуре будут иметь место, если добротность контура Q

больше единицы.

Для рассматриваемого контура можно построить резонансную кривую тока -

зависимость тока от частоты на основании формулы (3). Аналогичные кривые

можно построить и для напряжений на динамических элементах (L,C).

R 2 X 2

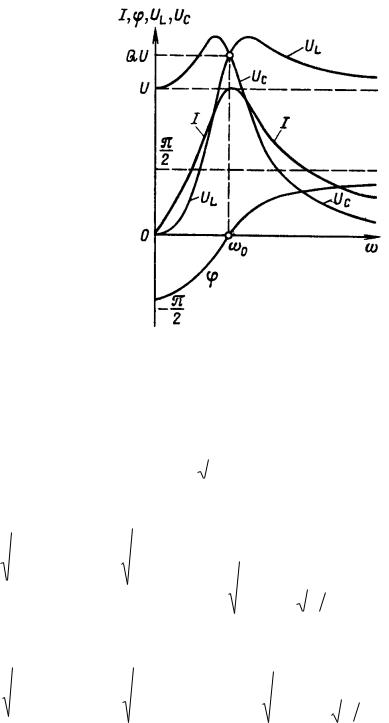
На рисунке 7 показаны резонансные кривые I f ( ),UL f ( ),UC f ( ) ,

f( ) для Q 1,25.

22

На рисунке 7 изображена также и фазо-частотная характеристика, из которой видно, что угол сдвига фаз между напряжением и током изменяется в пределах {-90 ;+90 } и достигает нулевого значения при резонансной частоте.

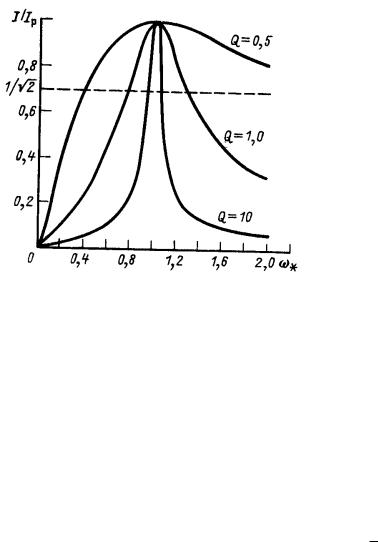
Рисунок 8

На рисунке 8 изображены графики резонансных кривых в относительных единицах. По оси ординат откладываем ток в долях от резонансного тока, а по оси абсцисс - частоту в долях от резонансной частоты. Чем меньше активное сопротивление резонансного контура при неизменных остальных параметрах схемы,

т.е. чем больше добротность контура Q, тем более острой (пикообразной) становится форма кривой тока I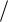 I рез f ( ) , где 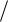рез .

Для оценки избирательных свойств цепи вводят понятие полосы пропускания

- полоса частот, на границах которой отношение I I рез составляет 12 =0,707. На рисунке 6 проведена горизонтальная прямая на уровне I I рез = 0,707 , ее пересечение с резонансными кривыми определяет граничные частоты полосы пропускания контура и, следовательно, ширину полосы пропускания. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания.

6.2Резонанс токов в пассивных двухполюсниках.

Резонанс токов наблюдается в электрической цепи с параллельно соединенными участками, обладающими индуктивностью и емкостью и образующими

24

параллельный колебательный контур, который получает энергию от источников синусоидального напряжения, последовательно соединенного с контуром.

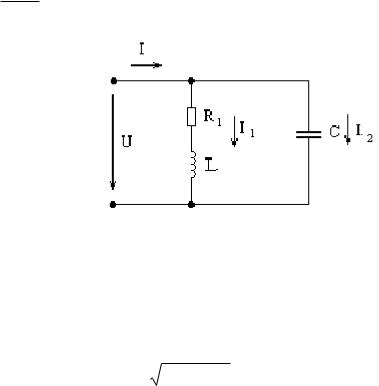
Рассмотрим явление резонанса токов в цепи, изображенной на рисунке 9. Пусть первая ветвь содержит активное R1 и индуктивное ωL сопротивление, а вторая ветвь

1

– емкостное C .

Рисунок 9

Если к цепи, изображенной на рисунке 1, приложено синусоидальное напряжение

Из формулы (39) видно, что ток на входе цепи может:

1)отставать от приложенного напряжения на угол φ, если B1 B2 , φ>0;

2)опережать приложенное напряжение, если B1 B2 , φ<0;

25

3) совпадать по фазе с приложенным напряжением, если B1 B2 , φ=0.

Резонанс токов в параллельном колебательном контуре возникает в момент,

когда реактивные проводимости ветвей будут равны между собой и полностью

компенсируют друг друга:

B B1 B2 0 или B1 B2 (40)

При этом противоположные по фазе реактивные составляющие токов равны

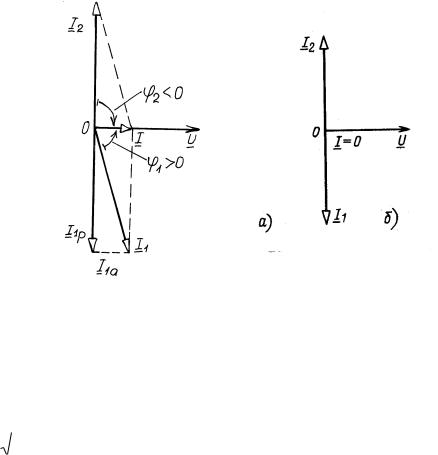
(рисунок 10а), поэтому резонанс в рассматриваемой цепи получил название резонанса токов. Из векторной диаграммы видно, что при резонансе ток I на входных выводах контура может быть значительно меньше токов в ветвях.

Рисунок 10

Условие резонанса токов можно записать следующим образом:

данном случае достаточно велико, что приведет к значительному увеличению напряжения в цепи.

26

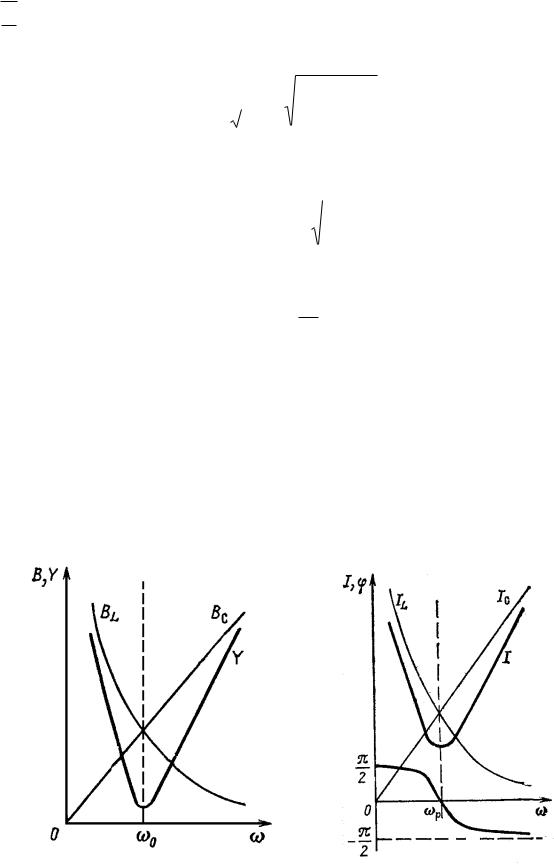
Резонанса токов можно достигнуть изменением , C, L или R1, но не всегда можно достигнуть резонанса изменением того или иного параметра, поэтому для достижения резонанса токов необходимо выполнение следующего условия:

R1 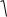CL .

Значение угловой резонансной частоты может быть получено из условия В=0.

Зависимости реактивных проводимостей и полной проводимости реального

колебательного контура от частоты приложенного напряжения источника

изображены на рисунке 11а. Емкостная проводимость В2=ВС с увеличением частоты

возрастает прямо пропорционально частоте, индуктивная проводимость В1=ВL

уменьшается обратно пропорционально частоте. При резонансе проводимости

равны, а полная проводимость равна (1/R1).

Рисунок 11

27

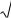
Резонансные кривые токов, изображенные на рисунке 11б, подобны графикам соответствующих проводимостей. При изменении частоты от 0 до < P сдвиг фаз между напряжением и общим током положителен и равен , при Р сдвиг фаз равен нулю (резонанс), при Р сдвиг фаз отрицателен и равен (рисунок

11б).

определить затухание цепи как длину отрезка этой прямой, заключенного между точками пересечения ее с резонансной кривой. Следовательно, чем меньше затухание, тем острее резонансная кривая и тем резче выражен резонанс. Отрезок прямой, характеризующий затухание, определяет полосу пропускания контура.

7 Методы анализа цепей синусоидального тока и напряжения.

Все принципы и методы расчета линейных цепей постоянного тока применимы к линейным цепям переменного тока одной частоты при переходе к комплексным уравнениям цепей переменного синусоидального тока.

Порядок анализа цепи методом комплексных амплитуд.

1)Выбираем условно положительное направление токов в каждой ветви и обозначаем их на схеме.

2)Замена гармонических токов и напряжений всех ветвей их комплексными изображениями (комплексными амплитудами или комплексными действующими значениями), а схемы замещения цепи для мгновенных значений – комплексной схемой замещения.

3)Составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений на основе законов Ома и Кирхгофа в комплексной форме.

4)Решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений.

5)Переход от комплексных изображений интересующих токов и напряжений к их оригиналам.

28

Результаты расчета наглядно иллюстрируются топографическими диаграммами.

Топографической называют векторную диаграмму напряжений, в которой каждой точке электрической цепи соответствует определенная точка векторной диаграммы.

При этом вектор, соединяющий две точки диаграммы, изображает напряжение между соответствующими точками электрической цепи. Примеры построения топографических диаграмм рассмотрены в примере расчета.

8 Измерение напряжения и тока.

Измерение напряжения и тока в цепях переменного тока производится

приборами различных систем, реагирующих на различные значения напряжений и токов.

приборы магнитоэлектрической системы реагируют на среднее значение измеряемого сигнала за период (постоянную составляющую)

приборы электродинамической и электромагнитной системы реагируют на действующее значение сигнала

приборы выпрямительной системы реагируют на средневыпрямленное значение сигнала

29

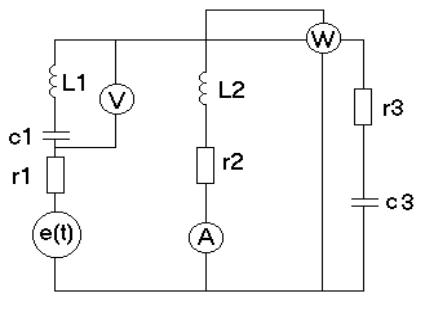
Пример. «Анализ линейной цепи с сосредоточенными параметрами при работе в режиме синусоидального тока».

Исходные данные:

r1 = 11 Oм ; L2 = 80 мГн; r2 = 11 Oм ; c1 = 300 мкФ;

r3 = 11 Oм ; c2 = 500 мкФ; L1 = 60 мГн ; w = 314 рад/с ; Em = 40 В

Задание.

1Определить токи и напряжения на элементах заданной схемы.

2Провести баланс мощности.

3Построить топографическую векторную диаграмму напряжений и векторную диаграмму токов.

4Определить показания приборов при условии, что амперметр и вольтметр электромагнитной системы.

5Определить все резонансные частоты в схеме.

Рисунок 1

Решение.

1 На схеме выберем условно положительные направления токов ветвей . Для определения токов в данной схеме необходимо рассчитать входное сопротивление:

30