
Вероятность избежать резонансного поглощения в гомогенной среде.
Энергетическая зависимость сечений взаимодействия нейтронов с тяжелыми ядрами имеют четко выраженную резонансную структуру. Резонанс в нейтронных сечениях наблюдается и у ядер со средними и малыми атомными весами, но главную роль в физике реакторов играют резонансные сечения тяжелых ядер, особенно 238U. В последующем изложении будем иметь в виду главным образом 238U, хотя все изложенное здесь будет справедливо и для смеси 232Th с делящимися изотопами.
Резонансные сечения, параметры резонансов.
Потенциальное рассеяние
При столкновении нейтрона с ядром, имеющим массовое число A, могут происходить взаимодействия двух типов. В первом случае нейтроны рассеиваются на ядре как на «твердом шарике», без проникновения в ядро и, тем самым, не возбуждая его «внутренних степеней свободы». Такой процесс носит название упругого потенциального рассеяния и его сечение p слабо зависит от энергии нейтронов (для 238U p=11 б).
Взаимодействие через составное ядро.
Однако
с некоторой вероятностью сталкивающийся
нейтрон проникает в ядро, образуя так
называемое «составное ядро» (A+1)
в возбужденном состоянии. Энергия
возбуждения составного ядра складывается
из энергии связи нейтрона в ядре
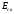 и кинетической энергии нейтрона
и кинетической энергии нейтрона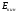 ,
то есть
,
то есть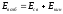 .
Возбуждение ядра оказывается довольно
сильным, поскольку
.
Возбуждение ядра оказывается довольно
сильным, поскольку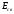 7
МэВ.
7
МэВ.
Атомное
ядро является квантовой системой с
определенными энергетическими уровнями
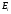 .
Когда
.
Когда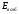 близко к одному из уровней
близко к одному из уровней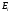 ,
вероятность образования составного
ядра резко возрастает, что приводит к
пикам в нейтронных сечениях. Положение
резонанса на оси кинетических энергий
нейтрона дается выражением
,
вероятность образования составного
ядра резко возрастает, что приводит к
пикам в нейтронных сечениях. Положение
резонанса на оси кинетических энергий
нейтрона дается выражением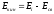 ,
а частота следования резонансов
определяется плотностью уровней ядра
(A+1).
,
а частота следования резонансов
определяется плотностью уровней ядра
(A+1).
Энергетические уровни составного ядра (A+1) не являются стационарными, имеют конечное время жизни и ядро распадается по одному из возможных каналов
|
|
|
A+n |
упругое резонансное рассеяние |
|
n+A |
(A+1) |
(A+1) + |
резонансный захват нейтрона |
|
|
|
A1 +A2 +n |
резонансное деление ядра |
В первом случае это упругое резонансное рассеяние sr, во втором – радиационное резонансное поглощение cr, в третьем – резонансное деление fr. Для 238U при резонансных энергиях открытые лишь первые два канала.
Конечное
время жизни (в соответствии с принципом
неопределенности
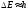 )
приводит к неопределенностям в положении
уровня и к конечной ширине резонансной
линии. Ширина уровня
)
приводит к неопределенностям в положении
уровня и к конечной ширине резонансной
линии. Ширина уровня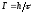 пропорциональна распаду составного
ядра в единицу времени. Если обозначить
вероятность распада ядра по каналу
пропорциональна распаду составного
ядра в единицу времени. Если обозначить
вероятность распада ядра по каналу как
как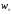 ,
то парциальные ширины будут равны
,
то парциальные ширины будут равны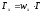 и
и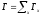 .
Для ядер238U
.
Для ядер238U
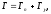 а для делящихся ядер
а для делящихся ядер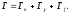 Ширина
Ширина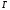 зависит
от индивидуальных характеристик
отдельных уровней и поэтому изменяется
от уровня к уровню. Однако усредненная
по нескольким уровням вблизи энергииE
ширина
зависит
от индивидуальных характеристик
отдельных уровней и поэтому изменяется
от уровня к уровню. Однако усредненная
по нескольким уровням вблизи энергииE
ширина
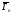 плавно изменяется с энергией по закону
плавно изменяется с энергией по закону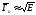 ,
поэтому величина
,
поэтому величина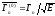 (приведенная нейтронная ширина) в среднем
слабо зависит от энергии резонанса.
Радиационная ширина
(приведенная нейтронная ширина) в среднем
слабо зависит от энергии резонанса.
Радиационная ширина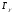 является суммой ширин, соответствующих
распаду возбужденного состояния ядра
является суммой ширин, соответствующих
распаду возбужденного состояния ядра
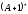 в низшие возбужденные состояния и потому
флуктуирует от уровня к уровню в гораздо
меньшей степени, чем
в низшие возбужденные состояния и потому
флуктуирует от уровня к уровню в гораздо
меньшей степени, чем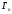 .
Для238U
.
Для238U
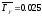 эВ.
эВ.
Формула Брейта-Вигнера.
В
простейшем приближении энергетическая
зависимость резонансного сечения вблизи
резонансной энергии
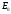 описывается формулой Брейта-Вигнера
описывается формулой Брейта-Вигнера
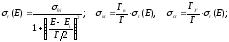 (14)
(14)
Частота
следования резонансов определяется
плотностью уровней составного ядра.
Среднее расстояние между резонансами
238U
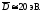 Величина резонансного сечения в
максимуме
Величина резонансного сечения в
максимуме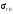 при малых энергиях резонансов весьма
велики, достигая приE10
эВ величины
10000 барн. С ростом энергии
при малых энергиях резонансов весьма
велики, достигая приE10
эВ величины
10000 барн. С ростом энергии
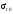 падает и при
падает и при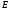
100 КэВ оказывается сравнимой с сечением
потенциального рассеяния p.
В действительности подобное сглаживание
резонансной структуры сечений происходит
при более низких энергиях (30
КэВ) за счет «доплеровского» уширения
резонансов.
100 КэВ оказывается сравнимой с сечением
потенциального рассеяния p.
В действительности подобное сглаживание
резонансной структуры сечений происходит
при более низких энергиях (30
КэВ) за счет «доплеровского» уширения
резонансов.
Резонансный интеграл
Пусть
мы имеем однородную бесконечную среду
– смесь резонансного поглотителя с
концентрацией
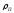 и сечением потенциального рассеянияp
и замедлителя с концентрацией
и сечением потенциального рассеянияp
и замедлителя с концентрацией
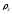 и сечением рассеянияs.
Полное сечение потенциального рассеяния
для такой однородной среды
и сечением рассеянияs.
Полное сечение потенциального рассеяния
для такой однородной среды
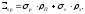 (15)
(15)
Рассмотрим
резонансное поглощение нейтронов при
замедлении на примере единичного
изолированного резонансного уровня
при энергии
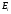 .
.
Введем следующие параметры резонансов:
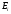 –энергия
резонансного уровня;
–энергия
резонансного уровня;
0i – сечение в центре резонансной линии при Ei ;
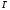 –ширина
резонанса;
–ширина
резонанса;
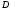 –расстояние
между резонансами.
–расстояние
между резонансами.
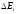 –эффективная
ширина резонанса, то есть область
энергий, где еще учитывается воздействие
резонанса на спектр нейтронов. Если
–эффективная
ширина резонанса, то есть область
энергий, где еще учитывается воздействие
резонанса на спектр нейтронов. Если
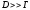 ,
то резонанс можно считать изолированным.
,
то резонанс можно считать изолированным.
Для одиночного изолированного резонанса справедлива формула Брейта-Вигнера
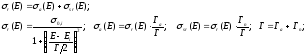 (16)
(16)
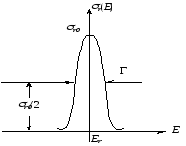
Рис.
2. Резонансная линия Брейта-Вигнера
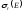 .
.
Er – точка максимума резонанса
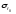 -
амплитуда резонансной линии
-
амплитуда резонансной линии
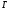 –ширина
резонанса на его полувысоте.
–ширина
резонанса на его полувысоте.
Как известно, в случае слабого поглощения среды поток нейтронов в ней описывается возрастным приближением, а вероятность избежать резонансного поглощения в возрастном приближении имеет вид
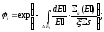 (17)
(17)
где
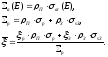 (18)
(18)
Сечение
потенциального рассеяния поглотителя
и замедлителя слабо меняются в пределах
резонансного уровня, поэтому величину
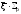 можно вынести из под знака интеграла.
В результате получим следующее выражение
можно вынести из под знака интеграла.
В результате получим следующее выражение
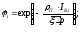 (19)
(19)
где
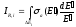 (20)
(20)
носит
название резонансного интеграла.
Заметим, что для одного резонансного
уровня
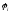 1
и
1
и
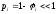 ,
где
,
где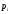 – есть вероятность нейтрону испытать
поглощение наi-ом
резонансе. Поэтому
– есть вероятность нейтрону испытать
поглощение наi-ом
резонансе. Поэтому
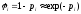 ,
,
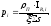 (21)
(21)
Вычислим резонансный интеграл для одиночного резонансного уровня
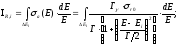 (22)
(22)
Если
область действия резонанса
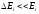 ,
то переменную
,
то переменную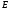 в знаменателе подынтегрального выражения
можно вынести из под знака интеграла,
присвоив ей значение резонансной энергии
в знаменателе подынтегрального выражения
можно вынести из под знака интеграла,
присвоив ей значение резонансной энергии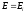
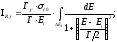 (24)
(24)
Производя стандартную замену переменных интегрирования
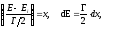
резонансный интеграл представим в виде
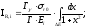 (25)
(25)
Пределы
интегрирования по переменной
 симметричны
относительно
симметричны
относительно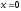 .
Наибольшее значение подынтегральное
выражение принимает в центре резонансной
линии
.
Наибольшее значение подынтегральное
выражение принимает в центре резонансной
линии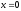 ,
и при энергиях, отличных от резонансной
энергии, это выражение стремиться к
нулю. Поэтому пределы интегрирования
можно распространить от -
до +,
так как основное значение интеграл
набирает в области
,
и при энергиях, отличных от резонансной
энергии, это выражение стремиться к
нулю. Поэтому пределы интегрирования
можно распространить от -
до +,
так как основное значение интеграл
набирает в области
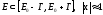
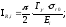 (26)
(26)
Однако, если концентрация резонансного поглотителя достаточно велика, поглощение в резонансе становится существенной величиной и поток нейтронов в районе резонанса сильно изменяется с энергией, поэтому возрастное приближение становится неприменимым для этого случая.
Приближение узких резонансов.
Резонанс считается сильным, если
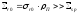 (27).
(27).
Для определения потока нейтронов в случае сильного резонанса рассмотрим газокинетическое уравнение замедления для однородной бесконечной среды. Для резонансов в области энергий от нескольких эВ до 10 КэВ, можно применить уравнение для асимптотической области энергий, в которую нейтроны попадают, совершив большое число рассеивающих столкновений:
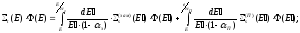 (28)
(28)
где
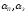 - максимальная потеря энергии при
рассеянии на ядрах урана и замедлителя
соответственно (
- максимальная потеря энергии при
рассеянии на ядрах урана и замедлителя
соответственно (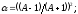 ).
Резонанс считается узким, если ширина
резонанса много меньше ступеньки
замедления, как для замедлителя, так и
для резонансного поглотителя, то есть
при выполнении условий
).
Резонанс считается узким, если ширина
резонанса много меньше ступеньки
замедления, как для замедлителя, так и
для резонансного поглотителя, то есть
при выполнении условий
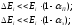 (29)
(29)
Так как резонанс узкий, то основной вклад в интеграл рассеяния вносит область энергий, далекая от резонансов. Для этих энергий поток нейтронов невозмущен резонансом и описывается распределением Ферми
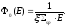 (30)
(30)
Принимая
это во внимание, при интегрировании по
энергии в правой части уравнения баланса
(28) положим
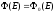 во всей области интегрирования. Кроме
того, будем считать, что в пределах всей
ступеньки замедления
во всей области интегрирования. Кроме
того, будем считать, что в пределах всей
ступеньки замедления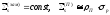 .
С учетом принятых упрощений, уравнение
для определения спектра нейтронов в
области резонанса примет следующий вид
.
С учетом принятых упрощений, уравнение
для определения спектра нейтронов в
области резонанса примет следующий вид
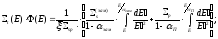 (31)
(31)
Интегрируя уравнение (31), и учитывая
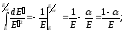
получим
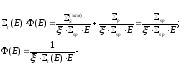 (32)
(32)
Это решение носит название спектра Вигнера, которое, в отличие от спектра Ферми, описывает спектр нейтронов в области действия сильного резонанса.
Вблизи резонанса t(E) резко возрастает, что приводит к падению потока резонансных нейтронов (E). Снижение потока нейтронов при резонансных энергиях приводит к уменьшению резонансного поглощения, причем тем большему, чем сильнее резонанс. В этом состоит эффект резонансного самоэкранирования или «резонансной блокировки».
РИСУНОК спектра Ферми и Вигнера
Для
вычисления вероятности избежать
резонансного поглощения на
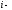 том
резонансе
том
резонансе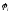 ,
воспользуемся выражением для величины
вероятности поглощения, в соответствии
с равенством:
,
воспользуемся выражением для величины
вероятности поглощения, в соответствии
с равенством:
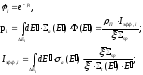 (33)
(33)
Величина
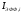 носит название эффективного резонансного
интеграла. Из выражения (33) следует, что
это есть резонансный интеграл от
некоторого эффективного сечения
резонансного поглощения, которое
отличается от истинного резонансного
сечения множителем
носит название эффективного резонансного
интеграла. Из выражения (33) следует, что
это есть резонансный интеграл от
некоторого эффективного сечения
резонансного поглощения, которое
отличается от истинного резонансного
сечения множителем
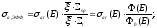 (34)
(34)
Таким
образом, эффективное сечение учитывает
депрессию потока нейтронов в сильном
резонансе. Пренебрегая интерференционным
членом потенциального и резонансного
взаимодействия, запишем
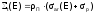 и подставим это выражение в (34)
и подставим это выражение в (34)
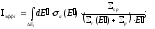 (35)
(35)
Произведем стандартную замену переменных,
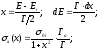
преобразуем выражение для эффективного резонансного интеграла
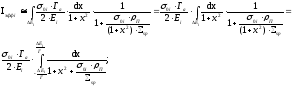 (36)
(36)
Обозначим
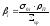 (37)
(37)
и введем новую переменную интегрирования
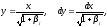
получим
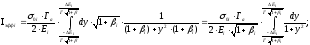
 Если
y>>1,
то
Если
y>>1,
то
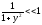 .
Поэтому, главный вклад в интеграл дадут
те значенияy,
для которых y1,
т.е. значения энергии в пределах
.
Поэтому, главный вклад в интеграл дадут
те значенияy,
для которых y1,
т.е. значения энергии в пределах
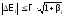 .
Последнее соотношение позволяет оценить
область действия резонанса по
энергетической шкале
.
Последнее соотношение позволяет оценить
область действия резонанса по
энергетической шкале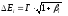 .
Таким образом, область действия резонанса
.
Таким образом, область действия резонанса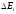 оказывается значительно больше истинной
ширины резонанса Г.
оказывается значительно больше истинной
ширины резонанса Г.
Так как резонанс изолированный, то пределы интегрирования можно распространить на интервал (-,), в результате получим окончательное выражение для эффективного резонансного интеграла
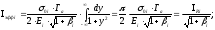 (38)
(38)
Нетрудно
заметить, что
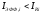 .
Фактор блокировки
.
Фактор блокировки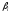 зависит от соотношения резонансного и
потенциального макросечения взаимодействия.
По этому параметру все резонансы можно
разделить на две группы: сильные и
слабые.
зависит от соотношения резонансного и
потенциального макросечения взаимодействия.
По этому параметру все резонансы можно
разделить на две группы: сильные и
слабые.
Слабый резонанс
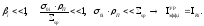 (39)
(39)
Таким образом, для слабого резонанса эффективный резонансный интеграл совпадает с резонансным интегралом. Это связано с тем фактом, что для слабого резонанса депрессия потока резонансных нейтронов практически отсутствует.
Сильный резонанс
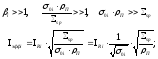 (40)
(40)
Величина
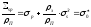 (41)
(41)
имеет
смысл сечения рассеяния гомогенной
среды, приходящееся на одно ядро
резонансного поглотителя, которая
зависит от разбавления
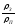 .
С ростом концентрации поглотителя
величины
.
С ростом концентрации поглотителя
величины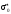 и
и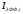 уменьшаются, хотя сама вероятность
избежать резонансного поглощения
растет, однако лишь как
уменьшаются, хотя сама вероятность
избежать резонансного поглощения
растет, однако лишь как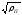 ,
в то время как для слабого поглощения
зависимость
,
в то время как для слабого поглощения
зависимость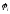 от концентрации резонансного поглотителя
носит линейный характер.
от концентрации резонансного поглотителя
носит линейный характер.
Эффект
самоэкранировки (блокировки) резонанса
оказывается весьма большим. Например,
для первого резонанса 238U
Ei=6.7
эВ, r0=23000
барн, так что при
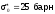 Iэффi
оказывается в 30 раз меньше IRi.
Iэффi
оказывается в 30 раз меньше IRi.
Ширина
действия резонанса может быть найдена
из условия
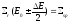 .
.
Подставляя выражение для r в форме Брейта-Вигнера
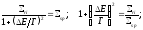 .
.
Считая
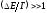 ,
получим
,
получим
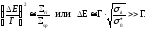 (42)
(42)
Эффективная ширина сильных резонансов мало меняется от резонанса к резонансу и составляет при небольших разбавлениях 1 эВ.
Интерполяционная формула для системы узких резонансов
Рассмотрим
замедление в среде с поглотителем,
имеющим резонансы при энергиях
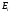 .
Если резонансы не перекрываются
(изолированные), то вероятность поглощения
нейтронов каждым из резонансов слабо
зависит от наличия других резонансов,
поэтому
.
Если резонансы не перекрываются
(изолированные), то вероятность поглощения
нейтронов каждым из резонансов слабо
зависит от наличия других резонансов,
поэтому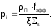 .
Тогда вероятность избежать резонансного
поглощения при замедлении на всей
совокупности резонансов
.
Тогда вероятность избежать резонансного
поглощения при замедлении на всей
совокупности резонансов
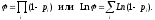
Считая
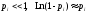 ,
так что
,
так что
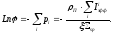 (43)
(43)
Таким
образом, в этом приближении эффективный
резонансный интеграл
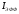 оказывается аддитивной величиной и
можно ввести суммарный эффективный
резонансный интеграл
оказывается аддитивной величиной и
можно ввести суммарный эффективный
резонансный интеграл
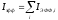 (44)
(44)
причем
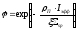 .
(45)
.
(45)
Разобьем
все множество резонансов на две группы:
сильные и слабые резонансы. Конечно,
граница между группами достаточно
неопределенна и зависит от концентрации
поглотителя
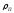 .
Пренебрегая этой зависимостью, получим
простейшую аппроксимацию для
.
Пренебрегая этой зависимостью, получим
простейшую аппроксимацию для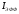
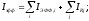 (46)
(46)
где
первая сумма берется по сильным резонансам
(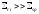 ),
а вторая по слабым (
),
а вторая по слабым (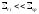 ).
Подставляя в (46 ) выражения (26) и (40),
получим
).
Подставляя в (46 ) выражения (26) и (40),
получим
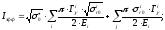
Каждая
из сумм является ядерной константой
для данного поглотителя, не зависящей
от его концентрации резонансного
поглотителя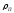 .
Обозначим их черезb
и
a
соответственно, тогда
.
Обозначим их черезb
и
a
соответственно, тогда
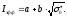
Константы a и b могут быть вычислены с помощью резонансных параметров или найдены путем обработки результатов измерений эффективного резонансного интеграла. Для 238U эта зависимость имеет вид
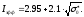
При
максимальной концентрации 238U
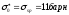 ,
так что минимальная величина
,
так что минимальная величина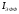 =10
барн, тогда какIR=280
барн. С разбавлением 238U
замедлителем
=10
барн, тогда какIR=280
барн. С разбавлением 238U
замедлителем
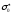 и
и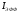 растут, но при очень малых концентрациях238U
сильные резонансы становятся слабыми
и полученная формула неприменима.
растут, но при очень малых концентрациях238U
сильные резонансы становятся слабыми
и полученная формула неприменима.
Приближение широких резонансов
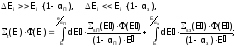
Для поглотителя
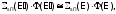
так как резонанс широкий, а для замедлителя

Зная спектр нейтронов в приближении широкого резонанса, можно получить выражение для эффективного резонансного интеграла в той же форме, как и для случая узкого резонанса
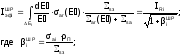
Сравнивая выражения для факторов блокировки для узкого и широкого резонанса, отметим, что для широкого резонанса не учитывается
Резонансное рассеяние нейтронов поглотителем
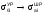
Потенциальное рассеяние нейтронов поглотителем
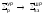
В приближении широких резонансов замедление на ядрах поглотителя не учитывается, так как считается, что масса поглотителя «бесконечно велика» и вклад поглотителя в формирование спектра нейтронов в области резонанса мал. В приближении узких резонансов влияние на спектр нейтронов в области резонанса тяжелых ядер поглотителя и легких ядер замедлителя как бы равновероятно.
Вводя в рассмотрение, как и для модели узкого резонанса, сечение рассеяния на одно ядро поглотителя
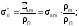 ,
(54)
,
(54)
эффективный резонансный интеграл в модели широкого резонанса можно представить в той же форме, как и в модели узкого резонанса
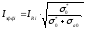 (55)
(55)
Главные отличия приближения широкого резонанса (иначе, бесконечной массы поглотителя) заключаются в том, что
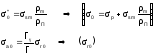 (56)
(56)
