
- •Пояснительная записка к дипломному проекту на тему: «вязкое затухание звуковых волн в сильных центробежных полях»
- •Оглавление
- •Глава 1 Литературный обзор 7
- •Глава 1 Литературный обзор
- •Поведение газа в центробежном поле сил
- •Волны в сильном центробежном поле
- •1.3.Затухание звуковых волн
- •Глава 2 Расчетная часть
- •2.1 Постановка задачи
- •2.2 Теоретический анализ
- •2.3 Описание программы
- •2.4 Верификация
- •2.5 Расчёт
- •Список литературы
Волны в сильном центробежном поле
Рассмотрим газовую центрифугу, являющуюся
ярким примером сильного центробежного
поля. Роторы газовых центрифуг вращаются
с линейной скоростью несколько сотен
метров в секунду [20]. Центробежное
ускорение может достигать порядка
 6gна радиусе ротора в несколько сантиметров,
что создает радиальный разделительный
эффект в газовой центрифуге. Тем не
менее, эффективное разделение изотопов
в промышленных центрифугах достигается
не только за счет центробежного поля.
Результирующую роль играет осевая
циркуляция, умножающая радиальный
эффект разделения. Вследствие механического
торможения газа, одной из причин
возникновения циркуляции газа являются
отборники, предназначенные для удаления
обогащенной и обедненной газовой смеси.
6gна радиусе ротора в несколько сантиметров,
что создает радиальный разделительный
эффект в газовой центрифуге. Тем не
менее, эффективное разделение изотопов
в промышленных центрифугах достигается
не только за счет центробежного поля.
Результирующую роль играет осевая
циркуляция, умножающая радиальный
эффект разделения. Вследствие механического
торможения газа, одной из причин
возникновения циркуляции газа являются
отборники, предназначенные для удаления
обогащенной и обедненной газовой смеси.
Пара отборников, расположенная около торцевых крышек центрифуги, также способствует образованию сильных ударных волн (Рис.4), распространяющихся вдоль оси центрифуги. Они могут отражаться от торцевых крышек формируя волны, бегущие в обоих направлениях вдоль оси вращения. Амплитуда ударных волн затухает довольно быстро. В большей части ротора мы имеем дело с волнами небольшой амплитуды, что позволяет рассмотреть их в первую очередь в линейном приближении.

Рис.4. Схема газовой центрифуги с отборниками. Сплошная линия – ударная волна, образованная отборником; пунктирная линия – волна, отраженная от верхней торцевой крышки.
Даже рассматривая волны в линейном приближении возникает ряд сложностей. Применение обычных уравнений для расчета скоростей в данном случае попросту невозможно. Во-первых, сильное центробежное ускорение порядка 106 gрезко изменяет характеристики линейных волн, во-вторых, сильный радиальный градиент плотности, меняющийся на 6 порядков за изменение радиуса порядка нескольких сантиметров, дает скорость поглощения, изменяющуюся на 6 порядков. В таких условиях применение уравнений Навье-Стокса возможно только в узкой области с размером 1-2 см, хотя, как известно, типичный радиус центрифуги 6-8 см. При меньшем радиусе газ становится настолько разреженным, что длина пробега его молекул превышает радиус ротора. В этой области гидродинамические уравнения не работают. Из-за этих причин невозможно оценить даже длину распространения волн.
Предложено следующее решение данной проблемы [].Необходимо использовать упрощенную модель газа, предполагая, что гидродинамические уравнения справедливы везде. Кроме того, рассматриваем случай бездиссипативного газа, что означает пренебрежение молекулярной вязкостью и теплопроводностью.
Рассмотрим идеальный газ, имеющий молярную массу Mи вращающийся с угловой скоростьюω. Система уравнений определяющая поведение газа во вращающейся системе запишется следующим образом []:
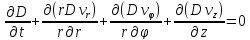 (1)
(1)
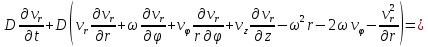
 (2)
(2)
 (3)
(3)
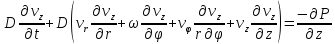 (4)
(4)
 ,
(5)
,
(5)
где
 – теплоемкость при постоянном давлении,P- давление,D- плотность,
– теплоемкость при постоянном давлении,P- давление,D- плотность, – температура и
– температура и –радиальная, угловая и осевая компоненты
скорости.
–радиальная, угловая и осевая компоненты
скорости.
Параметры газа могут быть представлены суммой параметров твердотельного вращения и неких отклонений:
 ,
(6)
,
(6)
где
 ,
, ,
, – давление, плотность и температура
твердотельного вращения, соответственно,
– давление, плотность и температура
твердотельного вращения, соответственно, ,
, ,
,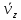 ,
, ,
,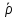 ,
,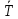 – отклонения радиальной, угловой, осевой
компонент скорости, давления, плотности
и температуры от значений твердотельного
вращения, соответственно.
– отклонения радиальной, угловой, осевой
компонент скорости, давления, плотности
и температуры от значений твердотельного
вращения, соответственно.
Зависимости от радиуса давления и плотности при твердотельном вращении имеют вид:
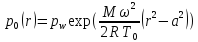 ,
(7)
,
(7)
 ,
(8)
,
(8)
где, a– радиус ротора,
а и
и – давление и плотность газа на стенке,
соответственно.
– давление и плотность газа на стенке,
соответственно.
Плотность идеального газа равна:
 (9)
(9)
Для отклонения плотности газа от твердотельного вращения имеем:
 (10)
(10)
Предполагая, что волны осесимметричны и делая ряд преобразований с уравнениями (1)-(10) [], получаем:
 (39)
(39)
Где
 (33)
(33)
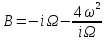 (36)
(36)

Для удобства введем
 .
После подстановки получим:
.
После подстановки получим:
 (40)
(40)
Где
 (41)
(41)
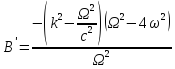 (42)
(42)
Анализ уравнений 39, 40 показывает, что в газовой центрифуге образуются волны трех семейств (рис.4), два семейства, названные верхним и нижним, при условии А≠0, и одно, названное звуковым, для условия А=0. Рассмотрим их более подробно.
Рассмотрим сначала первые два семейства. При условии А≠0 решение
уравнения 40 будет выглядеть как [22]:
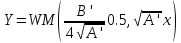 (45)
(45)
Где
 функция Уиттекера, удовлетворяющая
условию
функция Уиттекера, удовлетворяющая
условию
 .
.
Граничное условие
 дает нам дисперсионные соотношения для
дает нам дисперсионные соотношения для ,
и все возмущения выражаются через
,
и все возмущения выражаются через следующим образом:
следующим образом:
 (46)
(46)
 (47)
(47)
 (48)
(48)
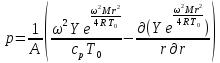 (49)
(49)
 (50)
(50)
Функция
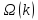 изображена на рис.5. Линии для условий
изображена на рис.5. Линии для условий и
и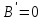 также показаны на рис.5. Условие
также показаны на рис.5. Условие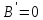 дает две линии:
дает две линии: и
и ,
последнее – закон дисперсии обычных
звуковых волн. Условие
,
последнее – закон дисперсии обычных
звуковых волн. Условие дает линию
дает линию ,
которая находится ниже линии
,
которая находится ниже линии для любого реального газа с показателем
адиабаты λ<2. В данном случае в качестве
рабочего газа используется
для любого реального газа с показателем
адиабаты λ<2. В данном случае в качестве
рабочего газа используется с показателем адиабаты λ=1,67. Параметры
рабочего газа указаны в таблице 1.
с показателем адиабаты λ=1,67. Параметры
рабочего газа указаны в таблице 1.
Таблица 1.
|
Параметр |
Значение |
|
M |
352 г/моль |
|
a |
0,065 м |
|
|
2π×1700
|
|
T0 |
300 K |
|
ρw |
80 мм рт. ст. |
|
cp |
385 Дж·K/кг |
|
c |
86 м/с |

Рис.5.
Закон дисперсии для первых четырёх
радиальных мод волн верхнего и нижнего
семейства (линии 1-4). Линия 5 – закон
дисперсии обычных звуковых волн Ω=kс,
линия 6 показывает условие .
.
Волны образуемые при выполнении условия
А≠0 делятся на две семьи, верхнюю с Ω>ckи нижнюю, для которой Ω<ck..
Рис. 5 показывает только первые 4 радиальные
моды волн в зависимости от волнового
вектора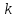 ,
направленного вдоль оси вращения.
Согласно рисунку линии верхнего семейства
стремятся к линии 5 при росте
,
направленного вдоль оси вращения.
Согласно рисунку линии верхнего семейства
стремятся к линии 5 при росте .
При
.
При их фазовые скорости стремятся к скорости
звука, а при
их фазовые скорости стремятся к скорости
звука, а при выполняется условие
выполняется условие .
.
Если
 ,
то мы имеем выражение для
,
то мы имеем выражение для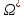 :
:


