Глава 2 Расчетная часть

2.1 Постановка задачи

Перейдём теперь непосредственно к постановке и решению задачи. Для этого рассмотрим цилиндрическую трубу (ротор), заполненную гексофторидом урана , которая вращается с угловой скоростью ω. Длина ротора L намного больше, чем его радиус r (L>> r), что позволяет считать ротор бесконечным (Рис.6.). Предполагаем, что температура T на внешней стенке постоянна и равна 300 K.Внутри ротора находится источник, который генерирует звуковые волны c волновым вектором k направленным вдоль оси Z. 

Рис.6. Цилиндрическая вращающаяся трубаНеобходимо разработать численный метод расчёта коэффициента затухания звуковых волн для вышеописанной модели и исследовать зависимости глубины проникновения звуковой волны от её волнового вектора, а также от радиуса и скорости вращения ротора.

Фундамент исследования составила работа [16] в которой предложен метод верификации, основанный на полуаналитическом решении задачи о циркуляции газа в роторе бесконечной длины. Поставленная задача решается с гармоническим возмущением малой амплитуды во вращающемся газе. В работе также показано, как решение системы уравнений в частных производных сводится к решению системы однородных дифференциальных уравнений, которые могут быть решены почти с любой точностью на персональном компьютере.

Запишем основную систему дифференциальных уравнений во вращающейся цилиндрической системе координат, описывающих движение в роторе [10]:

,

,

,

,

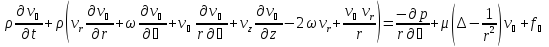вместе с плотностью и давлением, которые в данной модели подчиняются следующим распределениям:

, (28)

, (29)

где – давление и плотность на стенке ротора, соответственно,

образуется система уравнений, которая численно решается с помощью Maple при граничных условиях скользящей стенки:

=

=0

и граничных условиях трения на стенке:

.

Сравнение результатов, полученных с помощью данной полуаналитической модели и результатов численного моделирования, полученных в среде ANSYS CFX, показывает, что результаты эквивалентны[16].

2.2 Теоретический анализ

Получим теперь аналитическое выражение для декремента затухания волн, поляризованных вдоль оси вращения в центробежном поле сил. Для этого запишем систему уравнений для аксиальной компоненты скорости в цилиндрической системе координатах:

Подставляя выражение , и решая систему получим уравнение:

.

Решение которого будет состоять из общего однородного и частного неоднородного:

Решая общее однородное уравнение

получим:

Решая частное неоднородное уравнение

получим:

.

Их сумма запишется как:

Усредняя, получаем:

.

Так как энергия пропорциональна квадрату скорости, окончательно получим:

.

Зная, что вторая вязкость не внесёт значительного вклада, а теплопроводность на этом этапе мы не учитываем, то запишем формулу (19) без второй вязкости и теплопроводности:

.

Запишем коэффициент поглощения звуковых волн в единицу времени:

.

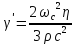Принимая во внимание то, что k=ω/cи перейдя к единым обозначениям получим выражение для энергии:

,

где ,, а– нормировочная постоянная,

которое принимает вид резонансной кривой.

Теперь перейдем к выводу коэффициента затухания звука в центробежном поле сил. Для этого запишем общий вид коэффициента затухания звука в трубе без вращения [10]:

,

где .

Для вращающейся системы:

,

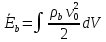где .

Следовательно, коэффициент затухания звуковых волн в центробежном поле сил будет равен:

,

откуда, после преобразований, получаем:

. (30)