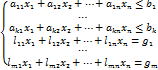методы оптимизации шпоры

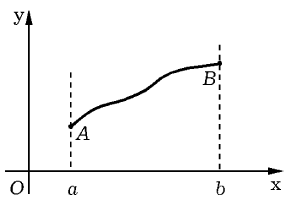
1. Общая постановка задачи математического программирования.

Задача формулируется таким образом: среди элементов , образующих множество X, найти такой элемент, который доставляет минимальное значение заданной функции . Для корректной постановки задачи требуется задать допустимое множество X (с помощью ограничений), целевую функцию , а также критерий поиска (минимум/максимум). Тогда решить задачу означает либо найти такое , при котором . В случае, если множество X является множеством всех возможных значений, то это задача безусловной оптимизации, в обратном случае – условной.

Порядок поиска решений:

1. Поиск всех точек стационарности

2. Выбор тех, что принадлежат области допустимых решений

3. Проверка граничных точек.

Сложность решения зависит от размерности. Например, может потребоваться проверить условие на границе, заданной линией, т.е. в бесконечном количестве точек.

Задача на условный экстремум включает ограничения: - это ограничение типа равенство.

Этап поиска условий экстремума – обычно аналитический, а вычисления оптимальных решений – инженерный.

Найти наибольшее и наименьшее значения y при ограничениях:

,i=1,2,…,k; , j=1,2,…,l;

Ограничения бывают типа равенств и неравенств.

2.1 Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.

Требуется найти экстремум функции , которая зависит от n переменных и эти переменные связаны m соотношениями , причем m<n, иначе решение было бы тривиальным. Для решения методом неопределенных множителей Лагранжа составим функцию .

Составим систему из n+m уравнений, приравняв нулю частные производные функции Лагранжа по и . Если полученная система имеет решения относительно своих параметров, то точка x может быть решением исходной задачи, то есть условным экстремумов.

На картинке изображены линии уровня при условии . Данное уравнение задает кривую S.

2.2 Пример. Найти экстремум функции при ограничении .

Составляем функцию Лагранжа , откуда

Правда, можно было решить проще: выразить из ограничений одну переменную через другую, подставить в функцию и найти экстремум функции одной переменной: например .

3. Линейный функционал.

Функционалом называют отображение, аргументов которого является функция вещественной переменной, а результатом – вещественное число. Функционал обозначим . Функционал является линейным, если он удовлетворяет принципу суперпозиции: .

Другое определение: функционалами называются величины, значение которых определяются выбором одной или нескольких функций. Пример: длина дуги пространственной кривой, соединяющей заданные точки.

Исторические предпосылки введения функционалов:

1. Геодезические линии. Найти линию минимальной длины между двумя точками при некотором условии.

2. Изометрическая задача. Найти замкнутую линию заданной длины, ограничивающей максимальную площадь. Условие на постоянство длины кривой называется изопараметрическим.

3. Задача о брахистохроне. На плоскости, требуется попасть из одной точки в другую без начальной скорости и только за счет силы тяжести за минимальное время.

Функционал непрерывен, если малому изменению соответствует малое изменение функционала. Функции можно считать близкими, если мал модуль их разности при любом x из области определений. Но так как часто функционал зависит еще от производных, желательно считать близкими функции, также близкие по своим производным (1-й порядок близости).

4. Понятие вариации функционала.

Вариация функционала позволяет определить экстремум функционала. Вариация функционала обозначается как и выглядит как приращение к «точке» (то есть функции, так как у нас исходная часть – не функция, а функционал) . Такое приращение называется вариацией аргумента и оно должно принадлежать тому же выбранному линейному нормированному пространству. Необходимое условие экстремума заключается в равенстве нулю вариации функционала. Проще говоря – как бы мы не толкали наши функцию, она в любом случае будет иметь один и тот же знак, то есть будет сидеть в экстремуме.

5. Вычисление вариации функционала.

Для вычисления вариации функционала запишем:

где – линейный функционал относительно второго аргумента, – бесконечно малая величина высокого порядка. Учитывая свойство линейности функционала L, можно записать

При переходе получаем при .

6.1 Постановка задачи Эйлера.

Нужно найти функцию, которая соответствует критерию оптимальности.

Рассматривается функционал вида . Требуется провести через две заданные точки с координатами и такую кривую , которая доставила бы экстремум заданному функционалу. Вычислим вариацию рассматриваемого функционала:

6.2 где – вариация с границами .

Проинтегрировав по частям второе слагаемое, получим:

Тогда получим условие экстремума:

Основная лемма вариационного исчисления позволяет записать условие экстремума в виде дифференциального уравнение для искомой кривой:

. Кстати, может быть не очевидно, но . А уравнение это – уравнение Эйлера.

8. Пример использования уравнения Эйлера для поиска оптимального управления.

Пусть имеется динамический объект, описываемый дифференциальным уравнением . Требуется перевести за время T объект из состояния в состояние так, чтобы функционал имел минимальное значение. Решаем: представим функционал в виде, для которого можно сформулировать задачу Эйлера: . Дифференциальное уравнение Эйлера в данном случае является линейным, имеющим второй порядок: . Решая его и подставляя граничные значения , можно получить оптимальную траекторию движения, а затем уже и выразить оптимальное управление.

10. Уравнение Эйлера-Пуассона.

Рассматривается функционал вида , т.е. зависящий от старших производных.. На функцию наложены граничные условия: и такие же для . Используя рассуждения из билета 6, можно прийти к выводу:

11. Пример использования уравнения Эйлера-Пуассона в теории оптимального управления.

Пусть имеется динамическая система, описываемая уравнением . Требуется перевести систему из состояния в состояние за время так, чтобы функционал принимал бы минимальное значение. Уравнение Эйлера-Пуассона примет вид , общее решение которого выглядит как . Эти коэффициенты находятся с использованием заданных значений функции и ее производных при нулевом и конечном времени, а затем из этого выражается оптимальное управление.

12.1 Вариационные задачи с подвижными границами. Пример в теории управления.

Рассмотрим задачу об экстремуме функционала

Функция – дважды дифференцируемая. На допустимые функции нет ограничений в виде граничных условий. Подсчет вариации дает . Приравняв ее к нулю, чтобы найти экстремаль, получим выражение 1: , откуда выражение 2: . В то же время, если посчитать выражение 1 по частям:

12.2Интеграл в правой части равен 0 из выражения 2. Значит

Так как вариации в точках a и b могут меняться произвольно, можно записать:

Получили уравнение Эйлера с естественными краевыми условиями.

13. Вариационные задачи на условный экстремум.

Имеется функционал вида

Каждая из функций проходит через две заданные для нее точки, на функции наложены ограничения вида , кроме того имеются ограничения на концах отрезка. Требуется найти экстремум функционала.

Воспользоваться системой уравнений Эйлера не получится – она справедлива для независимых переменных . Для решения вводим множители Лагранжа в функционал, образуется новый функционал:

Находится экстремум этого функционала, оставляются функции , при которых достигается экстремум функционала. Условный экстремум исходного функционала вычисляется с использованием выделенных функций .

15. Пример использования множителей Лагранжа для поиска управлений.

Пусть имеется динамический объект, описываемый дифференциальным уравнением . Требуется перевести его из состояния в состояние за время так, чтобы функционал имел минимальное значение. Образуем с помощью множителей Лагранжа новый функционал: . Тогда система уравнений Эйлера имеет вид:

Исключая и получим дифференциальное уравнение для функции вида . Отсюда находим x и определяем оптимальное управление.

16. Понятие переменных состояния.

Наиболее полным описанием системы является форма Коши.

, и граничными условиями.

Величины называются переменными состояния. В частном случае, если система линейна:

Если линейная система стационарна, матрицы A и B не зависят от времени.

17. Постановка задачи оптимального управления.

Объект задается в форме Коши: система уравнений _, граничные условия и функционал, который требуется минимизировать при соблюдении ограничения на входное воздействие . Задача оптимального управления заключается в нахождении функции состояния и управления для времени , которые минимизируют функционал.

Такие задачи решаются с помощью принципа максимума Понтрягина, а также методом динамического программирования.

18. Линеаризация дифференциальных уравнений и ее использование при получении принципа максимума.

Пусть дифференциальное уравнение задано в виде . Известно, что для решением будет. Изменим несильно входное воздействие: .

Проведем линеаризацию в окрестности:

- малое приращение.

Так как - решение, то , откуда

- линейное дифференциальное уравнение I-го порядка с переменными коэффициентами, которые можно найти, посчитав производные выше.

19. 1Принцип максимума.

Это не вывод, просто поиск пути

Задача задана – см. 17

Введем дополнительную переменную :

тогда из следует что

Изменив немного входное воздействие , получим приращение функционала (его линейную часть). Введем вспомогательные вектора и Тогда приращение функционала можно записать как скалярное произведение: . Предлагается далее изменить вектор таким образом, чтобы скалярное произведение было постоянным на интервале . Пусть новый . Условие постоянства: . Производная произведения: .

19.2 Линеаризация j'ой компоненты вектора :

Подстановка равенства в предыдущее, за скобки можно вынести

откуда

называемые сопряженными уравнениями.

Введем некую функцию . Для того, чтобы управление было оптимальным, эта функция должна достигать наибольшего значения в любой момент времени по аргументу .

20. Теорема о числе переключений.

(теорема об n интервалах)

Если объект управления описывается линейным дифференциальным уравнением n порядка, корни его характеристического уравнения вещественные неположительные (могут быть кратными), то для оптимального управления необходимо и достаточно, чтобы на n интервалах управляющее воздействие было равно максимальному , а знаки чередовались (n-1) раз. Теорема значительно облегчает нахождение оптимального управления. т.к. исключает необходимость определения функций и их анализа.

21.1 Определение моментов переключения.

а) Разветвленная схема, - процентные составляющие управляющего воздействия

Это система уравнений в форме Коши.

По принципу максимума Понтрягина:

откуда

По теореме об n интервалах:

Таким образом, функция зависит от всех составляющих вектора :

Решением каждого из уравнений будет:

содержит константу интегрирования

Подставляя результаты в получаем:

21.2 Эта функция имеет действительных корней. Таким образом, для оптимального управления необходимо n интервалов максимального значения управления, при этом знаки на интервалах должны меняться раз.

Если в рассматриваемой структуре содержится k звеньев с одинаковым динамическим свойством (т.е. имеет одинаковые постоянные времени T), то количество интервалов будет равно . Количество одинаковых звеньев уменьшает количество интервалов управления.

б) Параллельная схема,

(уравнение 1)

Пусть начальное состояние ; конечное состояние находится в гиперплоскости, определяемой уравнением 1. Таким образом, задача является задачей с подвижным правым концом.

21.3 Как в вопросе а) получается решение:

Постоянные интегрирования выбираются из условия трансверсальности: вектор параллелен . Последний имеет одно и то же значение:

В момент окончания управления составляющие вектора должны быть равны составляющим вектора , т.е.

для всех

Отсюда находим:

Подставляя результаты в , получаем:

Данная функция знака не меняет, т.к. значения экспонент возрастают при росте t, а коэффициенты при них положительны. Значит, попасть на гиперплоскость можно с помощью одного интервала управления при .

22.1 Принцип оптимальности.

Пусть движение системы описывается конечно-разностным уравнением:

(уравнение 1)

где - временной интервал, , – значение координаты в дискретный момент времени. В начальный момент времени .

Обозначим , запишем (уравнение 1) в виде:

Функционал, минимизацию которого нужно обеспечить при оптимальном управлении, выражается суммой:

Оптимальный процесс будет определен, если будут найдены

22.2 значения управляющих воздействий во все дискретные моменты времени (постоянно на интервале), минимизирующие сумму функционала. При этом необходимо прохождение траектории через начальную точку.

Критерий оптимальности является сложной функцией большого числа переменных . Метод динамического программирования позволяет свести поставленную задачу к более простой: к последовательному вычислению некоторый функций только одной переменной.

При этом будем руководствоваться принципом:

• любой отрезок оптимальной кривой тоже оптимален;

• будущее поведение процесса не зависит от его предыстории.

Значит, для любой траектории каждый ее участок, связывающий любую точку этой траектории с конечной, является оптимальным (хотя это не относится к любому участку траектории вообще). Участи процесса будем рассматривать в последовательности, обратной из номеру.

Рассмотрим отрезок, соответствующий времени . Управление должно быть оптимальным,

22.3 значит . Выбираем такое, что оно минимизирует функционал: .

Обозначим - функция состояния системы в выбранный момент времени как функция величины .

Другими словами, имеем таблицу значений для различных аргументов и соответствующие этим аргументам оптимальным значениям управления.

Перейдем к предыдущему интервалу. Аналогично:

и .

На основании формулы конечно-разностных уравнений:

Минимизируем выбором упр. воздействия для каждого фиксированного .

И так далее. На каждом шаге минимизации определяется оптимальное значение, зависящее от координаты. Процесс расчета продолжается, пока не придет к начальному интервалу. На нем используется начальное условие и определяется начальное значение управляющего значения, а за ним и весь ряд управляющих значений.

С увеличением порядка системы быстро возрастает объем вычислений.

25. Постановка задачи линейного программирования.

Задача допускает строгое алгоритмическое решение и определяется таким образом: в многомерном пространстве определяется область допустимых решений с помощью линейных ограничений типа равенств и неравенств:

где – известные числа

Допустимое решение – это вектор , удовлетворяющий заданными выше ограничениями. Предполагается, что все составляющие вектора неотрицательны. Требуется найти такое допустимое решение, при котором линейная форма с известными численные коэффициентами принимает наибольшее (или наименьшее) значение.

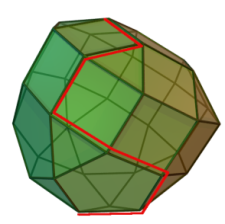
26. 1 Определение моментов переключения.

Для определения экстремальных точек сперва определим выпуклое множество. Множество M будет выпуклым, если две любые точки A,B, принадлежащих множеству M, определяют отрезок прямой, целиком принадлежащий множеству M.

Если наше выпуклое множество является кругом, то экстремальными точкам являются все точки на его окружности. В случае, если наше выпуклое множество – многоугольник, то экстремальными точками являются все углы. Таким образом, чтобы точка была экстремальной, требуется, чтобы она лежала на отрезке, стягивающемся в точку, математически: . Теорема: Точка x является экстремальной тогда и только тогда, когда перестановка столбцом матрицы А может быть представлена в блочном виде (где N – произвольная матрица) так, что , где – невырожденная квадратная матрица порядка m, и .

26.2 Например, имеется система уравнений . Для этой системы . Сперва положим , тогда , . Фактически это решение в случае . Так как в решении присутствуют отрицательные значения, то оно не является экстремальным (и вообще, не принадлежит множеству значений данной системы уравнений). После перестановки в уравнении переменных местами можно получить экстремальные решения. Сам займись. Кстати, число экстремальных точек не превышает величины , то есть возможного количество перестановок столбцом матрицы A. А еще у всякого непустого множества есть хотя бы одна экстремальная точка. И, кстати, линейная форма достигает наименьшего/наибольшего значения именно в экстремальной точке.

27.1 Симплексный метод.

Можно определить оптимальное решение перебором всех экстремальных точек, подставляя в них решение, но это может быть громоздко для большого количества точек. Поэтому есть более удобный способ – симплексный метод. Его суть заключается в нахождении хотя бы одной экстремальной точки, а затем передвижения от нее к другим точкам, пока такое движение будет возможно. Исчезновение этой возможности означает, что точка – оптимальна (минимальна/максимальна). Для начала путем теоремы об экстремальных точках (см. 26) находим одну из точек. Например, требуется найти наименьшее значение линейной формы при ограничениях . Найдем экстремальные точки, выбрав свободные переменные равными 0.

27.2

Выберем первую точку, значение линейной формы в ней будет . Можно ли найти точку со значением линейной формы меньше? Перепишем ограничения в виде

Переменные, имеющие значения в исходной экстремальной точки, называются базисными, а нулевые переменные – свободными. Решая систему относительно базисных переменных, получим: