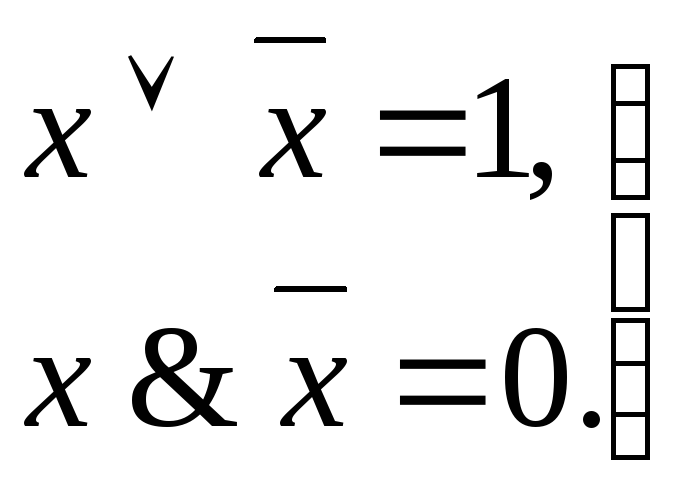1.6 Элементарные функции алгебры логики

В число функций алгебры логики, подсчитываемых с помощью теоремы 1, входят как функции, существенно зависящие от всех паргументов, так и функции, для которых часть из этих аргументов являются фиктивными.

Теорема 2. Число всех функций алгебры логики, существенно зависящих отпаргументов, определяется следующим рекуррентным соотношением:

.

(1.17)

В этом соотношении A_iесть число функций алгебры логики, существенно зависящих отiаргументов. Правая часть соотношения есть разность между числом всех функций алгебры логики и суммой всех функций алгебры логики, зависящих существенно от любого числа аргументов, меньшего чемп. Справедливость приведенного соотношения очевидна.

Рассмотрим одиннадцать функций, которые играют большую роль в построении теории функций алгебры логики и ее приложениях. Эти функции мы будем называть в дальнейшем элементарными.

Рассмотрение множества элементарных функций алгебры логики начнем со случая п=0. В силу теоремы 1 в этом случае имеются только две функции, совпадающие с константами 0 и 1:

Обе эти функции мы будем считать элементарными.

Для п=1, согласно теореме 1, имеем 2²=4 различные функции, представленные в таблице 1.6.

Таблица 1.6 –

0 1	0 0	1 1	0 1	1 0

В этом случае только функции f₃иf₄существенно зависят отх₁, а для функцийf₁иf₂этот единственный аргумент является фиктивным.

Эти две функции определяются таблицей 1.7

Таблица 1.7 – Логические функции повторения и отрицания

0 1	0 1	1 0

Эти две функции мы также причислим к элементарным, будем их называть функциями повторения и отрицания и записывать следующим образом:

(читается “неx”).

Найдем число функций алгебры логики, существенно зависящих от двух и трех переменных.

Из примера (таблица 1.6) вытекает, что А₀=2 иА₁= 2. Применяя теорему 2, имеем:

,
.

В случае п= 2 в силу теоремы 2 имеем десять различных функций, существенно зависящих от аргументовх₁их₂. Из этих десяти функций к элементарным функциям будем относить следующие семь функций (таблица 1.8):

Таблица 1.8 – Элементарные логические функции двух переменных

0 0 1 1	0 1 0 1	0 1 1 1	0 0 0 1	1 0 0 1	1 1 0 1	1 0 0 0	1 1 1 0	0 1 1 0

Функция f₅, определяемая этой таблицей, носит название дизъюнкциих₁их₂или логического сложениях₁их₂. Для ее обозначения применяются следующие символы:

и
.

Мы на протяжении всего дальнейшего изложения будем называть функцию f₅ дизъюнкцией и обозначать дизъюнкциюх₁их₂при помощи символа +.

Функция f₆носит название конъюнкции или логического умножениях₁их₂. Для ее обозначения применяется символ

Вместо этого символа часто применяют точку или вообще опускают всякий знак между х₁их₂, т. е.

.

В дальнейшем там, где это необходимо, будем употреблять для конъюнкции символ &, а в остальных случаях всякий знак между х₁их₂будем опускать.

Функция f₇носит название функции эквивалентности или функции равнозначности. Для ее обозначения применяются следующие два символа:

и
.

В дальнейшем будем называть эту функцию эквивалентностью х₁их₂. Для ее обозначения будем употреблять первый из двух вышеприведенных символов.

Функция f₈носит название импликациих₁вх₂. Она обозначается следующим образом:

.

Функция f₉носит название функции Вебба и обозначается следующим образом:

.

Функция f₁₀называется функцией Шеффера и обозначается следующим образом:

.

Функция f₁₁обычно называется функцией сложения по модулю два (реже ее называют функцией разноименности). Для ее обозначения употребляются символы

и
.

В дальнейшем будем употреблять для обозначения функции сложения по модулю первый символ .

Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения ,и сложения. Легко убедиться в том, что для этих функций имеют место сочетательный:

;
,

переместительный:

;

и распределительный законы конъюнкции относительно дизъюнкции:

.

Кроме того, имеет место распределительный закон дизъюнкции относительно конъюнкции:

,

который не имеет места в обычной алгебре, так как если бы он существовал, то он бы имел следующий вид:

.

Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.

0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 0 0 0 1	0 0 0 1 1 1 1 1	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 1 1 1 1 1 1	0 1 0 1 1 1 1 1	0 0 0 1 1 1 1 1

Совпадение построенных таблиц доказывает наше утверждение.

Рассмотрим теперь ряд простых, но весьма важных соотношений:

	(1.18)
	(1.19)
	(1.20)
	(1.21)

Из (1.18) как следствие получаем:

Как обобщение получены следующие формулы, обычно называемые формулами де Моргана:

	(1.22)
	(1.23)

Рассмотренные одиннадцать функций позволяют строить новые функции алгебры логики двумя основными путями:

1) путем перенумерации аргументов;

2) путем подстановки в функцию новых функций вместо аргументов.

Функцию, полученную из функций f₁, f₂, …, f_kи путем применения (возможно многократного) этих двух правил, будем называть суперпозицией функций f₁, f₂, …, f_k._.

Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить другие функции алгебры логики, являющиеся суперпозициями этих функций. Используя таблицы состояния (истинности) можно задавать в них любую функцию.