4.2 Основные свойства временных булевых функций

По результатам предыдущего параграфа любая временная булева функция может быть представлена в виде

где φ_i(i = 0, 1, ..., s-1) есть функции алгебры логики. Любая функция алгебры логики может быть представлена либо в дизъюнктивной, либо в конъюнктивной совершенной нормальной формах. дадим следующие два определения.

Определение. Если во временной булевой функции все функцииφ_i(i = 0, 1, ..., s-1)представлены в ДСНФ, то соответствующее выражение для φназывается дизъюнктивной совершенной нормальной формой временной булевой функции φ.

Если во временной булевой функции все функции φ_i(i = 0, 1, ..., s-1) представлены в КСНФ, то соответствующее выражение для φназывается конъюнктивной совершенной нормальной формой временной булевой функции φ.

Из этих определений и соответствующих теорем для функций алгебры логики вытекает следующая теорема.

Теорема.Любая временная булева функция может быть представлена в ДСНФ или КСНФ.

Пример 4.4. Записать в ДСНФ и КСНФ следующую временную булеву функцию.

Составляем ДСНФ и КСНФ для φ₀иφ₁:

После этого пишем ДСНФ и КСНФ данной временной булевой функции φ:

В силу вышесказанного ясно, что задача минимизации временных булевых функций может быть решена с помощью средств, подобных тем, какие рассматривались для случая минимизации функций алгебры логики.

Пример 4.5. Рассмотрим следующую функциюφ(х₁,x₂, t).

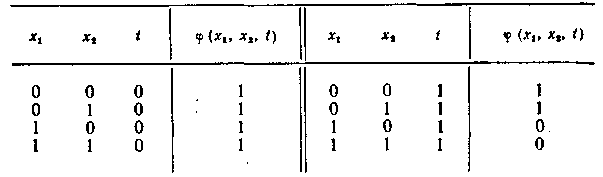
Согласно определению, получим ДСНФ этой функции:

Составим теперь минимизационную карту по методу неопределенных коэффициентов для φ, основываясь на принципе составления таких карт для функций алгебры логики, рассмотренном в гл. 1, и применим эту карту для минимизации данной функцииφ.

Согласно этой минимизационной карте, МДНФ функции φ имеет вид:

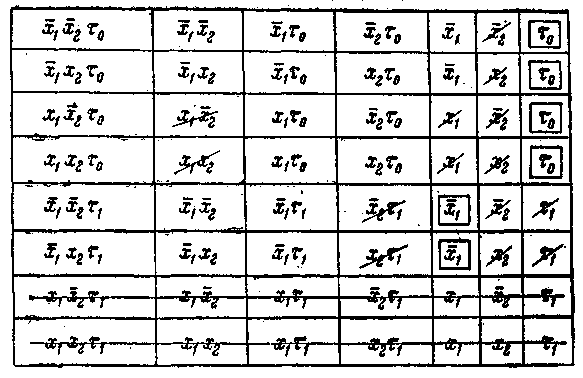
Рисунок 4.1 - Минимизационная карта к примеру 4.5

Пример 4.6. Применим теперь метод неопределенных коэффициентов для функции, рассмотренной в примере 4-4. Соответствующая МДНФ получена на основании минимизационной карты, приведенной на рисунке 4.2, и имеет вид:

Рисунок 4.2 - Минимизационная карта к примеру 4.6

Из приведенных примеров видно, что минимизационные карты в случае временных булевых функций достаточно громоздки и работа с ними при числе переменных х более трех или при большом количестве допустимых значений t затруднительна. В подобных случаях можно проводить неполную минимизацию. Неполная минимизация проводится следующим образом. Пусть ДСНФ временной булевой функции φ имеет вид:

Находим по обычным правилам МДНФ для φ₀, φ₁, φ₂, . . , φ_s-1 и за приближенное минимальное выражение для φ берем:

где - МДНФ функцииφ_i (i=0,1,...,s-1). При большом (s-1 ) и малом количестве аргументов х в функциях φ_i такой метод достаточно продуктивен.

Пример 4.7. Применяя метод неполной минимизации для функции примера 4.5, получим:

За неполную минимальную форму ВБФ принимаем выражение

Пример 4.8. Теперь применим метод неполной минимизации

для временной булевой функции примера 4.4:

Неполная минимальная форма для φ запишется в виде следующего выражения:

Пример 4.9. Найдем неполную минимальную форму для следующей временной булевой функции:

Выписываем ДСНФ для функций φ₀,φ₁, φ₂, φ₃;

После минимизации каждой из этих функций получим

В результате получаем минимальную форму для φ:

Применим теперь для функции φметод минимизирующих карт:

Таким образом, в этом случае приближенная минимальная форма оказалась МДНФ для данной функции. Для минимизации временных булевых функций, кроме метода минимизирующих карт, можно применять любые методы минимизации, рассмотренные для функций алгебры логики.