3.2 Теорема анализа и эквивалентные схемы

Рассмотрим решение задачи получения общей логической функции (или системы функций), отражающей структуру логической сети. Для логического (п, k)-полюсника эти функции имеют вид:

Система (3.1) называется системой собственных функций (п, k)-лолюсника. Таким образом, задача анализа данной схемы логической сети сводится к написанию системы собственных функций для этой сети.

Рис. 3-2.

Пример 5. На рис. 3.2 показана схема логического (4,2)-полюсника. Система собственных функций для этой сети будет:

Рис. 3-3.

Пример 6. На рис.3-3 показана схема логического (4,2)-полюсника, система собственных функций которого имеет вид:

Произведем преобразование этой системы функций:

Совпадение преобразованных собственных функций примера 6 с соответствующими функциями примера 5 показывает, что с точки зрения логического описания эти схемы логических сетей совпадают.

Определение. Две схемы логических сетей, у которых собственные функции эквивалентны, т. е. могут быть получены одна из другой с помощью эквивалентных преобразований, называются эквивалентными.

Схемы (4, 2)-полюсников рис. 3.2 и рис. 3.3 эквивалентны между собой. Подчеркнем, что собственные функции не определяют вид схемы логической сети, т. е. не обязательно являются структурными функциями. Эти функции описывают лишь логическую связь между множеством входов и множеством выходов схемы.

Рис. 3.-4.

В дальнейшем удобно несколько изменить правила геометрической интерпретации логических сетей. Во-первых, вместо обозначений вершин графа с помощью кружков будем использовать стандартные обозначения для наиболее часто встречающихся логических функций (эти обозначения приведены на рис. 3-4), при этом будем предполагать, что все логические элементы, кроме элемента, моделирующего функцию отрицания, имеют два входа (рис. 3-4).

Кроме того, в дальнейшем не будем указывать множество вершин, сопоставляемых множествам X иY. Эти вершины будут просто подразумеваться. Соответствующие стрелки, идущие от вершин множестваX к вершинам множества А и от вершин множестваА к вершинам множестваY, будут обрываться, а у места обрыва будет указываться вершинаX илиY, с которой связано это ребро. Наконец, не будем ставить там, где это не вызывается особой необходимостью, номера вершинА.

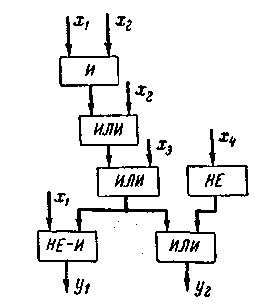
Рис. 3-5.

В соответствии с этими изменениями на рис. 3-5 изображена схема логической сети, представленная ранее на рис. 3-2.

Подчеркнем, что анализ схемы дает однозначное написание ее собственных функций и это написание отражает структуру схемы. Особенно наглядна связь между написанием собственных функций и структурой схемы, если пользоваться скобочной формой записи.

Пример 7. Для схемы, изображенной на рис. 3.5, скобочная запись «от входов к выходам» выглядит следующим образом:

Эта запись полностью определяет структуру соответствующей схемы логической сети. Другими словами, для скобочной записи собственных функций «от входов к выходам» можно установить взаимнооднозначное соответствие между этой записью и структурой схемы логической сети .

Анализ реальных схем с точки зрения логики их работы проводится в два этапа. Сначала из имеющейся принципиальной схемы удаляются все несущественные, вспомогательные элементы, которые не влияют на логику работы схемы, а служат для обеспечения устойчивости работы схемы, нормальной крутизны фронтов импульсов и т. д. После этого получаем схему, состоящую лишь из элементов, выполняющих логические функции, и связей между ними. Такая схема эквивалентна заданию некоторой схемы логической сети. Для ее анализа можно воспользоваться вышеизложенными соображениями.