Динамика твердого тела
Уравнения движения твердого тела
Твердое тело – это тело, расстояния между точками которого не меняется.
Твердое тело – механическая система с 6 степенями свободы
для описания его движения требуется 6 скалярных уравнений или 2 векторных уравнения:
|
|
dvC |
|
|
(e) |
– теорема о движении центра масс |
|
m |
dt |
F |
|
||||
|
|
||||||
|
dL |
M |
(e) |
|
– уравнение моментов |
||
|
dt |
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
L, M – а) относительно неподвижного начала или центра масс; б) относительно подвижного начала с v = vC.
Динамика твердого тела
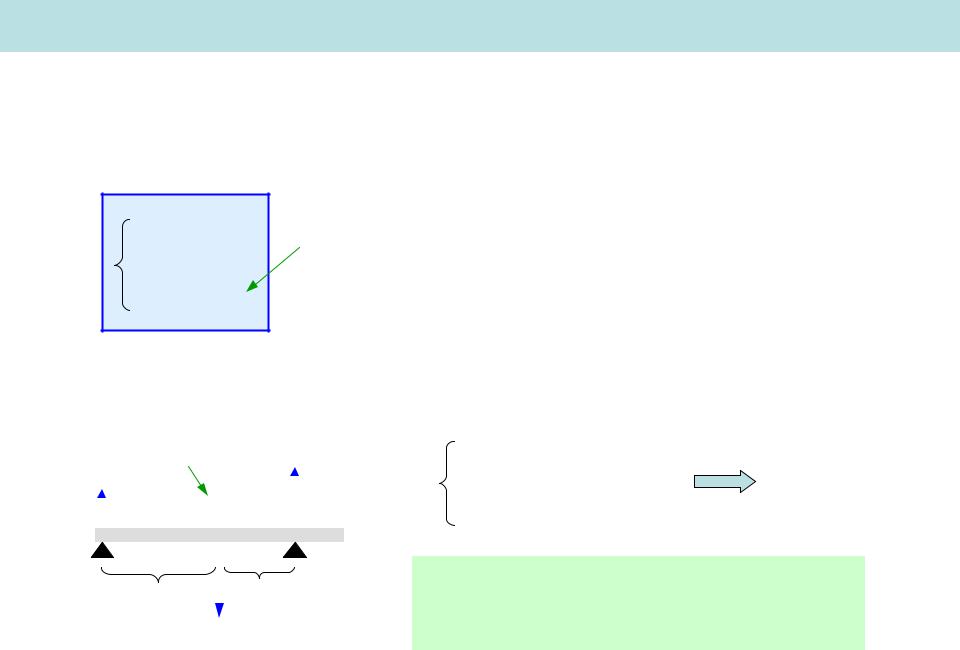
Равновесие твердого тела
Условия равновесия:
F (e) 0 |
M(e) = 0 относительно любого начала |
M (e) 0
Равновесие балки |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
центр масс |
|
|
N1 N2 mg 0 |
|
|
|
|
|
||||||
N1 |
O |
|
N2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
N1x1 N2 x2 0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
x2 |
|
|
|
|
x1 |
|
|
|
|
x1 |
|
x2 |
|
|
N1 |
|
|
mg |
N2 |
|
|
mg |
||
|
|
|
|
|
x1 |
x2 |
x1 |
x2 |
||||||||
|
|
|
mg |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Динамика твердого тела
Уравнение моментов относительно неподвижной оси
z – неподвижная ось |
|
|
(ось моментов) |
dL |
|
Уравнение моментов |
M |
|
O |
dt |
|
|
|
При проецировании на ось z
dLz |
M z |
– уравнение моментов относительно |
dt |
|
неподвижной оси |
|
|
|
В цилиндрической системе координат
Lz mv |
M z F |
Динамика твердого тела
Уравнение моментов относительно неподвижной оси
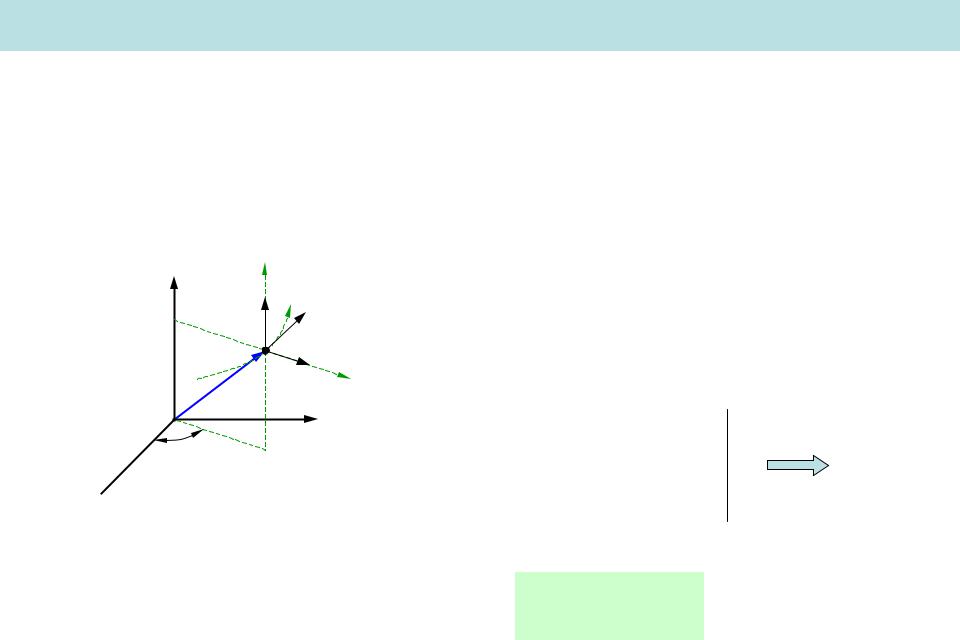
Цилиндрическая система координат
( , , z) – координаты в цилиндрический системе координат
|
z |
|
ez |
e |
|
|
|
||
|
|
|
|
|
z |
|
|
|
|
|
r |
|
e |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
x
x cos y sin z z
e , e , ez – локальные координатные орты (направлены в сторону увеличения соответствующей координаты)
|
e |
e |
ez |
M z (r F )z |
0 |
z |
|
|
F |
F |
Fz |
M z F
Динамика твердого тела
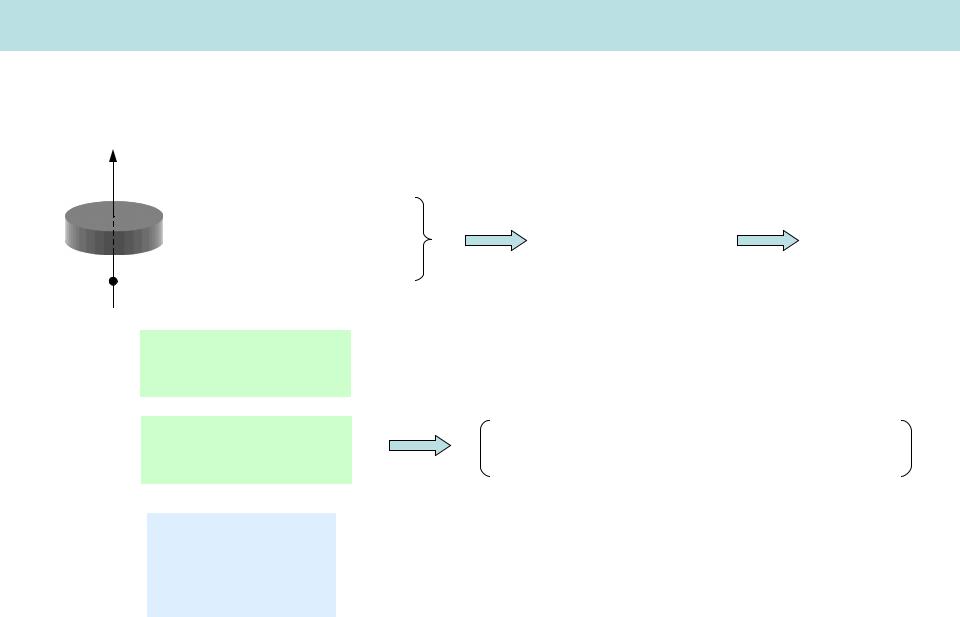
Уравнение динамики вращательного движения
– ось моментов
|
Lz imivi |
Lz mi i2 |
|
O |
vi i |
|
|
|
2 |
– момент инерции (характеризует инерционные |
|
|
Iz mi i |
свойства тела относительно данной оси вращения) |
|
|
|
||
Lz |
Iz |
из уравнения моментов относительно |
|
неподвижной оси |
|||
|
|
|
d |
(Iz ) M z |
– уравнение динамики вращательного |
|
|
движения вокруг неподвижной оси |
|
|
dt |
||
|
|
||
|
|
|
|
Mz – момент внешних сил относительно оси вращения
Динамика твердого тела
Уравнение динамики вращательного движения
Работа, совершаемая моментом силы
dA Fdr F(d r) d r F M zd |
dA M zd |
Кинетическая энергия твердого тела при вращательном движении
K |
1 |
mivi2 |
1 |
mi ( ri )2 |
2 |
mi ri2 |
K |
Iz 2 |
|
2 |
2 |
2 |
2 |
||||||
|
i |
i |
i |
|
Кинетическая энергия твердого тела
2 |
|
2 |
vC – скорость центра масс, |
|
K mvC |
|
IC |
IC – момент инерции относительно оси |
|
2 |
||||
2 |
|
вращения, проходящей через центр масс |
||
|
|
|
Динамика твердого тела
Теорема Гюйгенса–Штейнера |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
O |
|
|
A |
a, , ' – аксиальные вектора |
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
ось O || |
оси A |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
a |
|
|
|
|
2 |
( a) |
2 |
|
2 |
a |
2 |
2a |
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
dm |
|
|
|
2 |
dm |
|
|
2 |
|
|
2 |
dm 2a dm |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
IA |
|
dm a |
||||||||||
|
|
|
|
|
|
2dm |
I |
O |
|
|
dm m |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
Если O проходит через центр масс, то C 0 и
I A IC ma2 |
– теорема Гюйгенса-Штейнера |
|
|
Динамика твердого тела
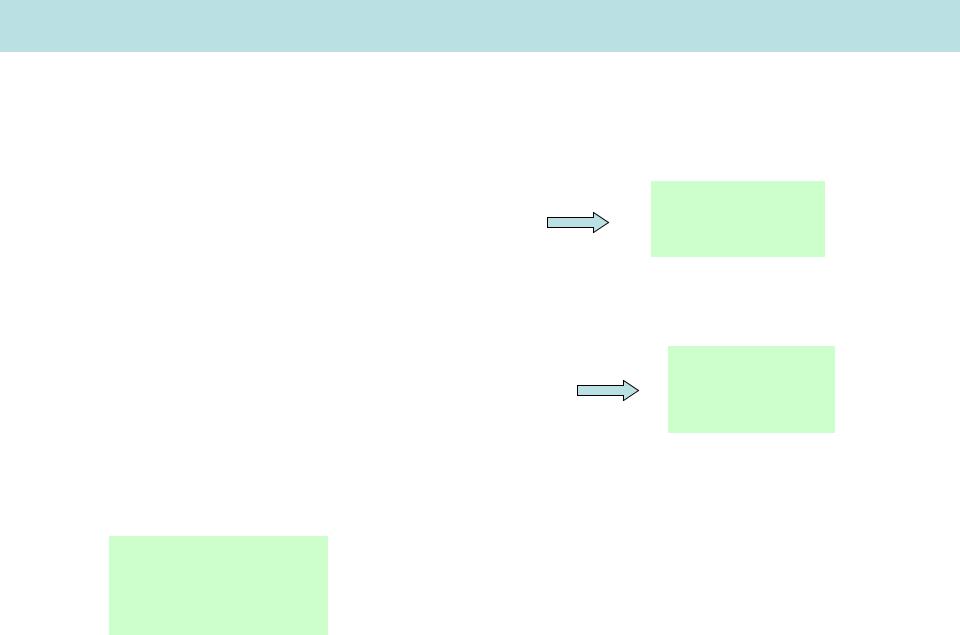
Вычисление моментов инерции
Общая формула I 2dm
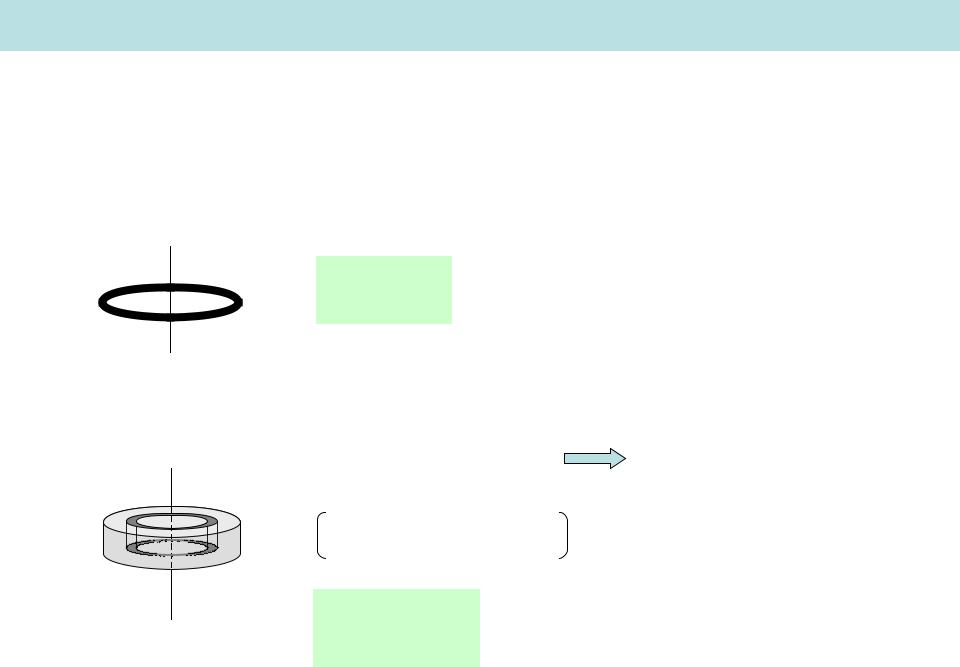
1) Кольцо
m, R
I mR2
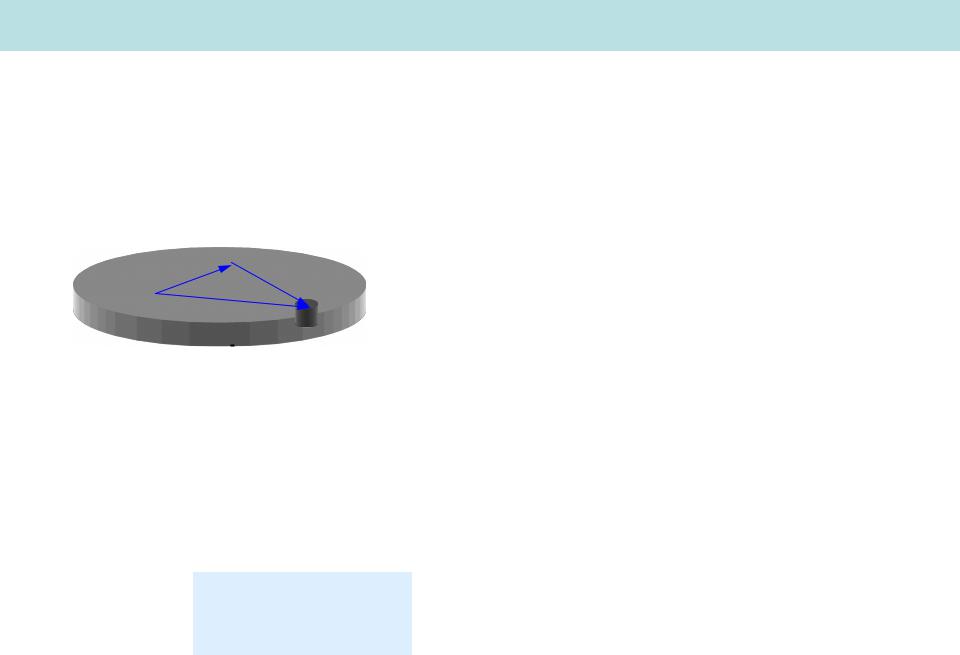
2) Диск (цилиндр) |
|
|
|
dm m dS |
2m rdr |
|
Диск = система колец |
|
|||||
m, R |
|
|
|
S |
|
R2 |
|
|
|
2m R r3dr |
1 mR2 |
||
dS 2 rdr, |
S R2 |
I |
||||
|
|
|
|
R2 0 |
|
2 |
I |
1 mR2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
Динамика твердого тела
Вычисление моментов инерции |
|
|
|
|
|
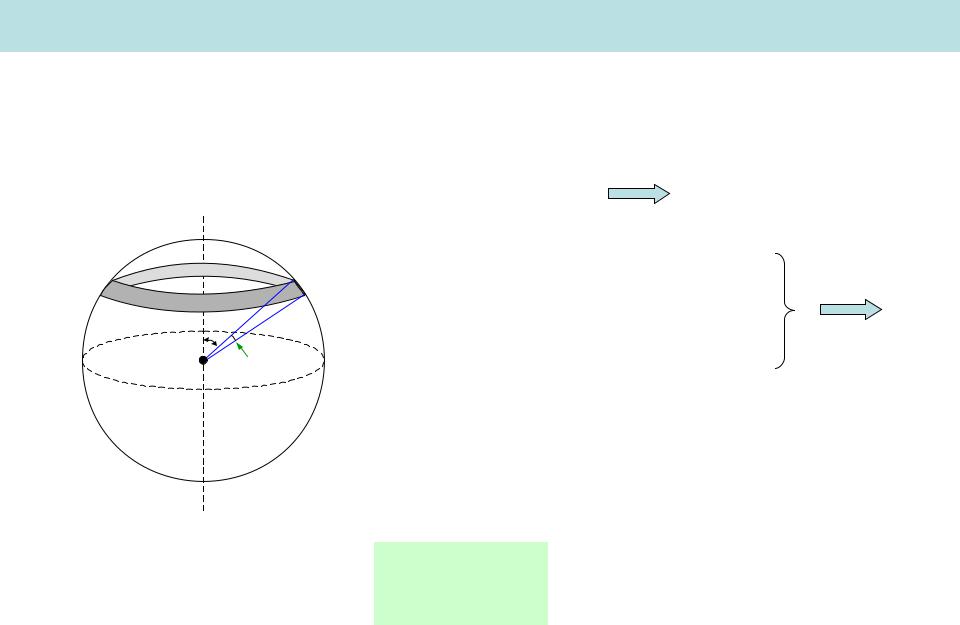
3) Сфера |
|
|
|
|
dS |
|
Сфера = система колец |
|
dm m |
||
|
|
S |
|||
|
|
|
|
||
m, R |
dS 2 (R sin )(Rd ) 2 R2 sin d |
|
|||
|
S 4 R2 |
|
|
|
|
r R sin |
|
|
|
|
|
d |
|
|
|
|
|
|
I r2dm |
1 mR2 |
|
2 mR2 |
|
|
sin3 d |
|
|||
|
|
2 |
0 |
3 |
|
I 23 mR2
Динамика твердого тела
Вычисление моментов инерции |
|
||
4) Шар |
|
|
dm m dV |
|
|
Шар = система сфер |
|
m, R |
|
dV 4 r2dr |
V |
|
|||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
V 43 R3
2 |
2m R |
2 |
I dI 3 r2dm |
R3 0 r4dr |
5 mR2 |
I 25 mR2