Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
При равновесии в газе устанавливается хаотическое (тепловое) движение молекул. Все направления движения равновероятны.
Давление газа
1)Все молекулы одинаковы
2)vi v
|
|
v x |
|
|
|
|
|
|
|
|
i ( x), ( y), ( z) |
3) |
v v y |
||
i |
|
|
|
|
|
v z |
|
|
|
|
|
|
n 1 n |
– концентрация молекул i-й скоростной группы |
|
|
i |
6 |
|
|
|
|
|
Термодинамика и статистическая физика
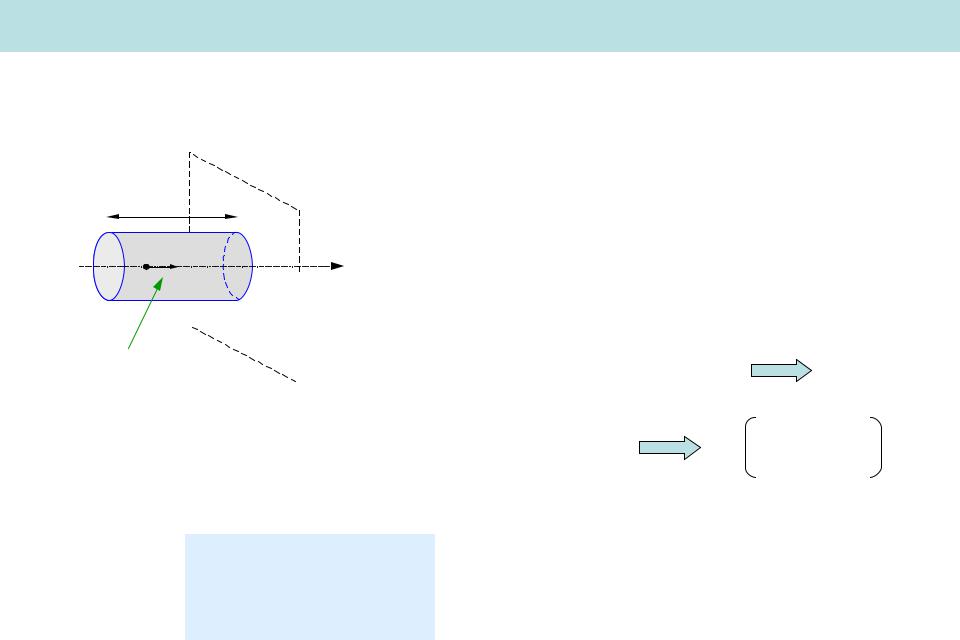
Основное уравнение молекулярно-кинетической теории газов
v t |
Число молекул, ударяющихся об S за t |
|
|
1 nSv t |
|
|
N |
|
|
|
6 |
|
|
|
|
S |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Они передадут импульс |
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
n( z ) |
1 n |
|
pz (2mv ) N |
1 nmv 2 |
S t |
|
||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
6 |
|
|
|
|
|
|
3 |
|
|
||
|
|
|
|
|
Fz |
p |
z |
1 |
nmv 2 S |
|
P |
Fz |
|
|
|
|
|
|
3 |
|
S |
||||
|
|
|
|
|
|
t |
|
|
|
|||
P |
1 nmv 2 |
|
2 n |
– основное уравнение МКТ |
|
3 |
|
3 |
|
|
|
|
|
|
Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
Свойства |
|
|
1) PV |
N |
RT |
|
||
|
NA |
|
P nkT
P 23 n
2)При равновесии в смеси газов
3)При тепловом равновесии газов
N |
n, |
k |
R |
|
V |
N A |
|||
|
|
23 kT
1 2 K
1 2 K
обладает свойствами температуры
Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
Распределении кинетической энергии по степеням свободы
Все направления движения равноправны |
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
vx2 v2y |
vz2 |
v2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
x |
|
y |
1 |
|
|
y |
1 kT |
|
|
|
|
|
|||||
|
|
z |
3 |
|
x |
z |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема о равномерном распределении кинетической энергии по степеням свободы:
Средняя кинетическая энергия, приходящаяся на одну степень свободы любой атомно-молекулярной системы, равна 12 kT
Число степеней свободы есть число независимых координат, заданием которых определяется пространственное положение системы
Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
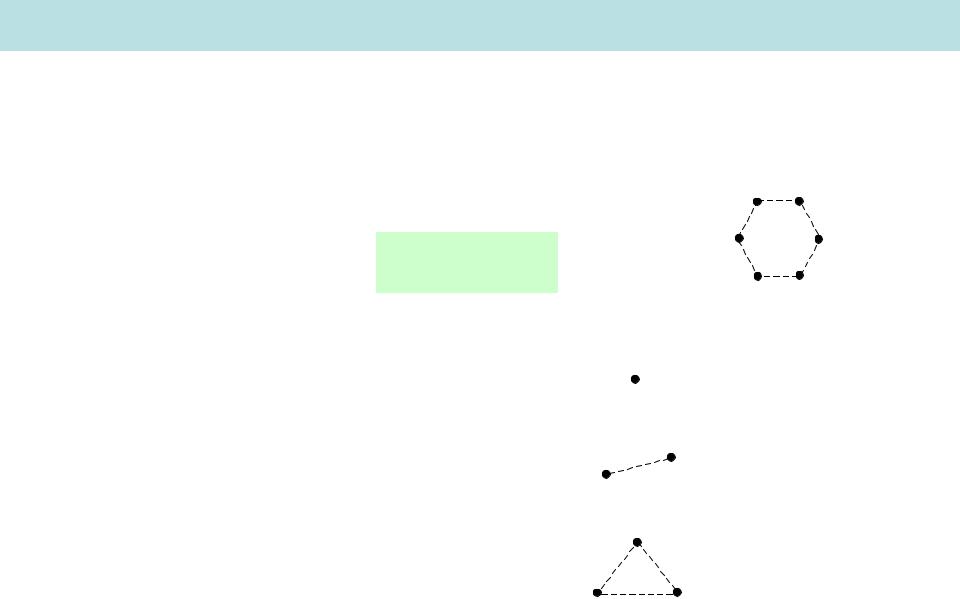
Число степеней свободы
Система N материальных точек с k связями (молекула)
Число степеней свободы |
f 3N k |
1) Одноатомная молекула |
f 3 |
2) Жесткая двухатомная молекула f 5
2) Жесткая трехатомная молекула f 6
Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
Газ жестких молекул
Вся энергия молекулы кинетическая |
(при равновесии) |
2f kT
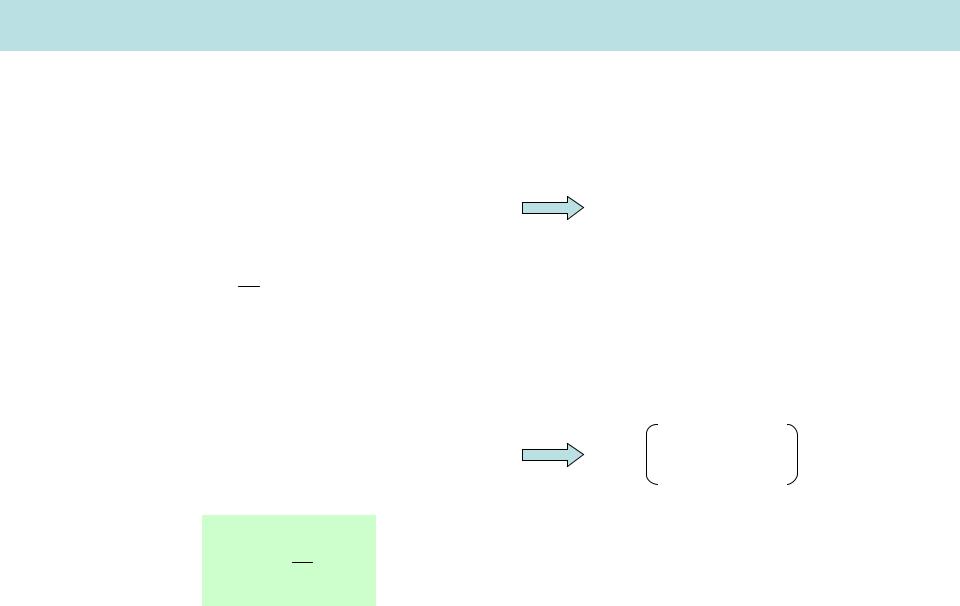
Внутренняя энергия одного моля идеального газа таких молекул
U N |
|
|
f |
N |
kT |
f |
RT |
C dU |
|
A |
|
|
|||||||
|
2 |
A |
2 |
|
V |
dT |
|||
|
|
|
|
|
|||||
CV 2f R
Термодинамика и статистическая физика
Основное уравнение молекулярно-кинетической теории газов
1)Теплоемкость газа одноатомных молекул ( f = 3 )
He, Ar, Ne и другие инертные газы
CV 23 R
2)Теплоемкость газа двухатомных жестких молекул ( f = 5 )
( при комнатных t ) O2, N2, H2 , воздух
CV 25 R
3)Теплоемкость газа трех- и более атомных жестких молекул ( f = 6 )
водяной пар H2O
CV 3R
Термодинамика и статистическая физика
Распределение Максвелла
При равновесии движение молекул беспорядочно Все направления движения равноправны
dP(vi ) (vi )dvi |
(i x, y, z) |
|
dP(vi ) |
– вероятность vi (vi ; vi dvi ) |
|
(vi ) |
– функция распределения (плотность вероятности) для vi |
|
Аналогично для трехмерной вероятности
dP(v) f (v) dvxdvydvz
dP(v) |
– вероятность v (v; v dv) |
f (v) |
– функция распределения (плотность вероятности) для v |
Термодинамика и статистическая физика
Распределение Максвелла
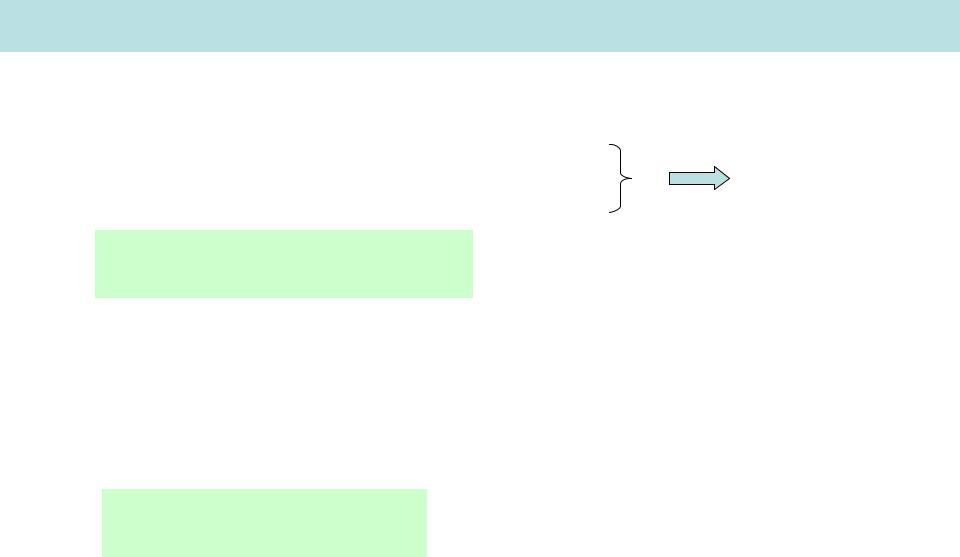
В предположении, что все направления движения статистически независимы
f (v) (vx ) (vy ) (vz )
и равноправны |
f (v) ® f (v) |
(v ) Ae vi2 |
(i x, y, z) |
|
i |
|
|
3 v2 |
|
|
f (v) A e |
|
|
|
|
|
Условие нормировки |
(vx ) dvx |
|
|
|
|
Средняя кинетическая энергия |
x |
|
f (v) (vx ) (vy ) (vz ) 
1
x (vx ) dvx 12 kT
Термодинамика и статистическая физика
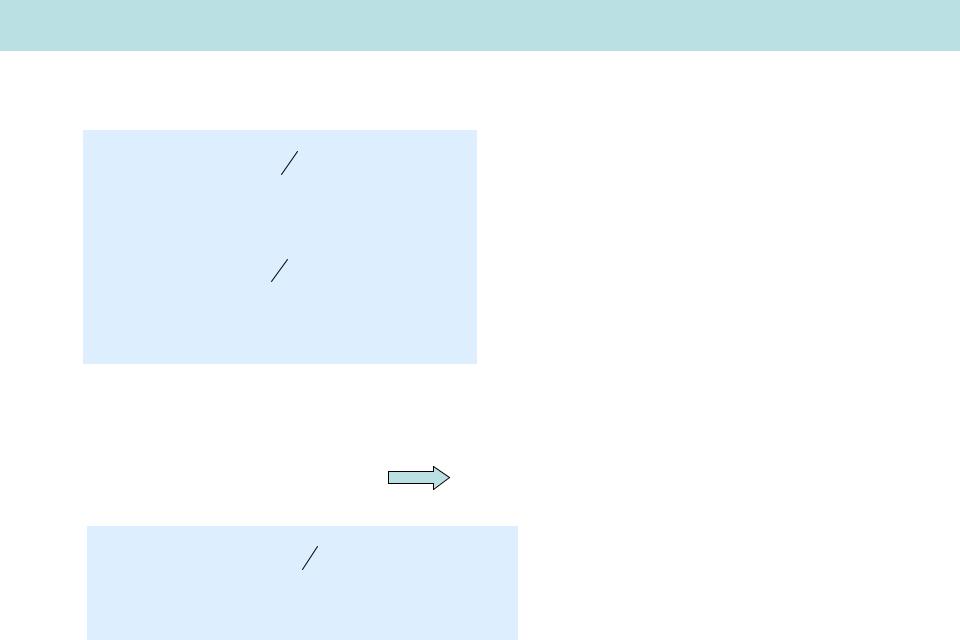
Распределение Максвелла
|
|
|
m |
|
12 |
|
|
mvx2 |
|
||||
(v |
x |
) |
|
|
|
|
exp |
|
|
|
|||
|
|
|
|
||||||||||
|
|
2 kT |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2kT |
– распределение Максвелла |
|||||
|
|
|
|
|
|
|
32 |
|
|
|
|
||
|
|
|
m |
|
|
|
mv2 |
|
|||||
f (v) |
|
|
|
|
exp |
|
|
|
|
||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
2 kT |
|
|
|
|
|
2kT |
|
||||
F(v) – плотность вероятности для модуля скорости, тогда
F(v)dv 4 v2 f (v)dv
|
m 32 |
|
2 |
|
|
mv2 |
||
F(v) 4 |
|
|
v |
|
exp |
|
2kT |
|
|
|
|||||||
|
2 kT |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|