8. Дифференциальные уравнения

231 - 240. Найти общее решение дифференциального уравнения.

231. а) (x²-y²)y' = 2xy, б) 2xy' -6y = -x².

232. а) (1+x²)y' -2xy = (1+x²)², б) (x²-1)y' +2xy² = 0.

233. а) xy' = y ln(y/x), б) xy' +y = y².

234. а) xy' +y = 3, б) y +y - xy' = 0.

235. а) xy' +x e^y/x -y = 0, б) xyy' = y²+1.

236. а) y' cos x = (y+1)sin x, б) xy' = y + x cos²(y/x).

237. а) ; б) .

238. а) x²y' +y = x+1, б) xy' =y ln²(y/x).

239. а) x²y' +y²-2xy = 0, б) xy' = 1+y².

240. а) xy' +y = x+1, б) xy' = y(y-1).

241. (1-x²)y'' = xy' . 242. 2yy'' +(y')²+(y')⁴ = 0.

243. y'' +y' tg x = sin 2x. 244. y'' +(1/x)y' = x².

245. 1+(y' )²+yy'' = 0. 246. (1+y)y'' -5(y')² = 0.

247. xy'' +2= x³. 248. y'' tg y = 2(y' )².

249. y'' -2y' tg x = sin x. 250. 3yy'' +(y')² = 0.

251 - 260. Найти частное решение дифференциального уравнения y'' +py' +qy = f(x), удовлетворяющее начальным условиям y(0) = y₀, y' (0)=y'₀.

251. y'' +4y' -12y = 8sin 2x; y(0)=0, y' (0)=0.

252. y'' - 6y' +9y = x²-x+3; y(0)=4/3, y' (0)=1/27.

253. y'' +4y = e^-2x; y(0)=0, y' (0)=0.

254. y'' -2y' +5y = xe^2x; y(0)=1, y' (0)=0.

255. y'' +5y' +6y = 12cos 2x; y(0)=1, y' (0)=3.

256. y'' - 5y' +6y = (12x-7)e^-x; y(0)=0, y' (0)=0.

257. y'' - 4y' +13y = 26x+5; y(0)=1, y' (0)=0.

258. y'' - 4y' =6x²+1; y(0)=2, y' (0)=3.

259. y'' -2y' +y = 16e^x; y(0)=1, y' (0)=2.

260. y'' +6y' +9y = 10e^-3x; y(0)=3, y' (0)=2.

261 - 270. Дана система линейных дифференциальных уравнений с постоянными коэффициентами

dx/dt = a₁₁x+a₁₂y,

dy/dt = a₂₁x+a₂₂y.

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

261. dx/dt = 4x+6y, 262. dx/dt = -5x-4y,

dy/dt = 4x+2y. dy/dt = -2x-3y.

263. dx/dt = 3x+y, 264. dx/dt = 6x+3y,

dy/dt = 8x+y. dy/dt = -8x-5y.

265. dx/dt = -x+5y, 266. dx/dt = 3x-2y,

dy/dt = x+3y. dy/dt = 2x+8y.

267. dx/dt = -4x-6y, 268. dx/dt = -5x-8y,

dy/dt = -4x-2y. dy/dt = -3x-3y.

269. dx/dt = -x-5y, 270. dx/dt = -7x+5y,

dy/dt = -7x-3y. dy/dt = 4x-8y.

9. Кратные, криволинейные и поверхностные интегралы

271 - 280. Изменить порядок интегрирования.

271. 272.

273. 274.

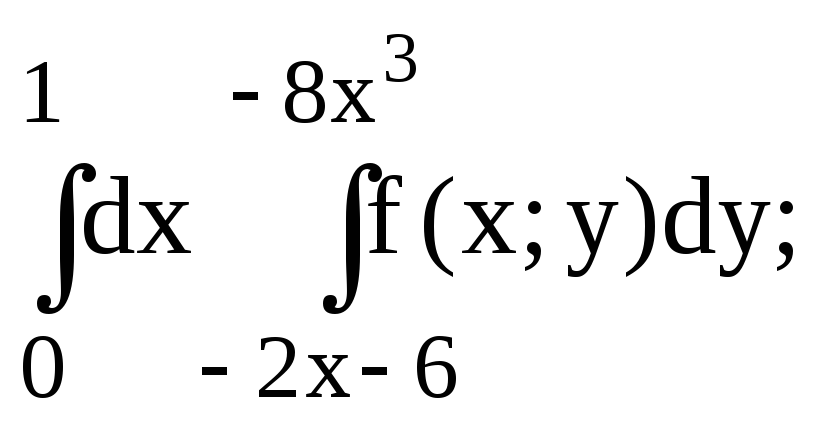
275. 276.

277. 278.

279. 280.

281 - 290. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy.

281.	z=0,	z=x, y=0, y=4, x= .
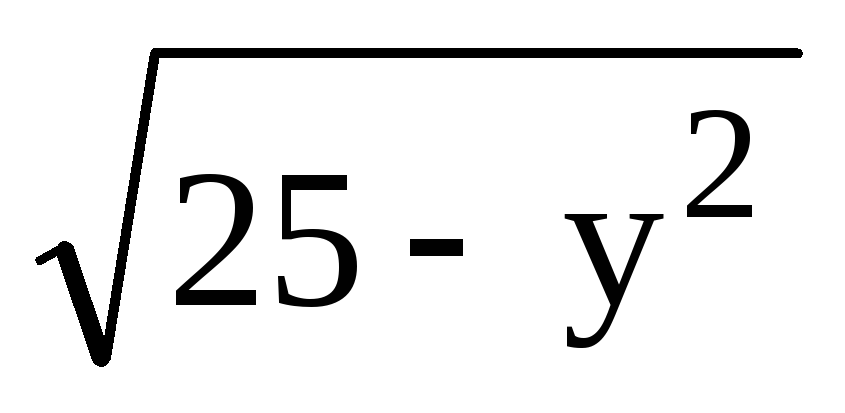282.	z=0,	z=9-y2, x2+y2=9.
283.	z=0,	z=4-x-y, x2+y2=4.
284.	z=0,	z=y2, x2+y2=9.
285.	z=0,	y +z=2, x2+y2=4.
286.	z=0,	4z=y2, 2x-y=0, x+y=9.
287.	z=0,	x2+y2=z, x2+y2=4.
288.	z=0,	z=1-y2, x=y2, x=2y2+1.
289.	z=0,	z=1-x2, y=0, y=3-x.
290.	z=0,	z=4 y, x=0, x+y=4.

291. Вычислить криволинейный интеграл

(x²-y)dx-(x-y²)dy

вдоль дуги L окружности x=5cos t, y=5sin t, обходя ее против хода часовой стрелки от точки А(5; 0) до точки В(0;5). Сделать чертеж.

292. Вычислить криволинейный интеграл

(x+y)dx-(x-y)dy

вдоль ломаной L=OAB, где О(0;0), А(2;0), В(4;5). Сделать чертеж.

293. Вычислить криволинейный интеграл

вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки, если А(1;0), B(1;1), C(0;1). Сделать чертеж.

294. Вычислить криволинейный интеграл

(x²-2xy)dx+(y²-2xy)dy

вдоль дуги L параболы y=x² от точки А(-1;1) до точки В(1;1). Сделать чертеж.

295. Вычислить криволинейный интеграл

(x²y-3x)dx+(y²x+2y)dy

вдоль верхней половины L эллипса x=3cos t, y=2sin t (0<t<). Сделать чертеж.

296. Вычислить криволинейный интеграл

(x²+y)dx+(y²+x)dy

вдоль ломанной L=ABC, где А(1;2), В(1;5), С(3;5). Сделать чертеж.

297. Вычислить криволинейный интеграл

.

Вдоль дуги L кривой y=e^-x от точки А(0;1) до точки В(-1;е). Сделать чертеж.

298. Вычислить криволинейный интеграл

dx - dy

вдоль отрезка L=AB прямой от точки А(1;2) до точки В(2;4). Сделать чертеж.

299. Вычислить криволинейный интеграл

вдоль дуги L параболы y=2x² от точки О(0;0) до точки А(1;2).Сделать чертеж.

300. Вычислить криволинейный интеграл

dx + xdy

вдоль дуги L кривой y=ln x от точки А(1;0) до точки В(е;1). Сделать чертеж.