тоэ / Лекция№43

Теория / ТОЭ / Лекция N 43. Сведение расчета переходных процессов в цепях с распределенными параметрами к нулевым начальным условиям.

С учетом граничных условий расчет переходных процессов в цепях с распределенными параметрами можно проводить как при нулевых, так и ненулевых начальных условиях. Однако в первом случае анализ осуществляется в целом проще, что определяет целесообразность сведения расчета к нулевым начальным условиям. Пример такого сведения на основе принципа наложения для задачи на подключение в конце линии нагрузки схематично иллюстрирует рис. 1, где в последней схеме сопротивление  имитирует входное сопротивление активного двухполюсника.

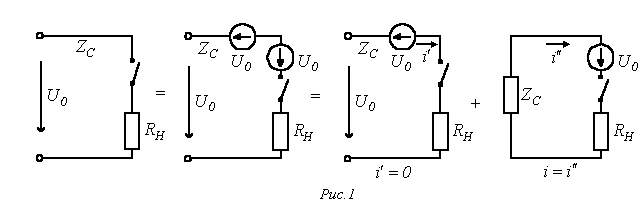
Таким образом, если к линии, в общем случае заряженной, подключается некоторый в общем случае активный двухполюсник, то для нахождения возникающих волн необходимо определить напряжение  на разомкнутых контактах ключа (рубильника), после чего рассчитать токи и напряжения в схеме с сосредоточенными параметрами, включаемой на это напряжение  при нулевых начальных условиях. Полученные напряжения и токи накладываются на соответствующие величины предыдущего режима.

При отключении нагрузки или участков линии для расчета возникающих волн напряжения и тока также можно пользоваться методом сведения задачи к нулевым начальным условиям. В этом случае, зная ток  в ветви с размыкаемым ключом (рубильником), необходимо рассчитать токи и напряжения в линии при подключении источника тока  противоположного направления непосредственно к концам отключаемой ветви. Затем полученные токи и напряжения также накладываются на предыдущий режим.

В качестве примера такого расчета рассмотрим длинную линию без потерь на рис. 2, находящуюся под напряжением , к которой подключается дополнительный приемник с сопротивлением .

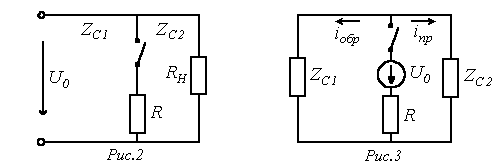
В соответствии со сформулированным выше правилом схема для расчета возникающих при коммутации волн будет иметь вид на рис. 3. Здесь

;

и в соответствии с законом Ома для волн

.

Соответствующие полученным выражениям эпюры распределения напряжения и тока вдоль линии представлены на рис. 4.

Отметим, что, поскольку

,

к источнику от места подключения нагрузки  пошла волна, увеличивающая ток на этом участке.

Если наоборот приемник с сопротивлением  не подключается, а отключается, то расчет возникающих при этом волн тока и напряжения следует осуществлять по схеме рис.5.

 

Правило удвоения волны

Для момента прихода волны к нагрузке можно записать

;

(1)

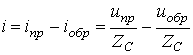
или

.

(2)

Складывая (1) и (2), получаем

.

(3)

Соотношению (3) соответствует расчетная схема замещения с сосредоточенными параметрами, представленная на рис. 6,б. Момент замыкания ключа в этой схеме соответствует моменту падения волны на нагрузку  в реальной линии. При этом, поскольку цепь на рис. 6,б состоит из элементов с сосредоточенными параметрами, то расчет переходного процесса в ней можно проводить любым из рассмотренных ранее методов (классическим, операторным, с использованием интеграла Дюамеля).

Следует отметить, что, если в длинной линии имеет место узел соединения других линий или разветвление, то в соответствии с указанным подходом эту неоднородность следует имитировать резистивным элементом с соответствующим сопротивлением, на который падает удвоенная волна.

Пусть, например, линия с волновым сопротивлением  разветвляется на две параллельные линии с волновыми сопротивлениями  и  (см. рис. 7,а). Узел разветвления в расчетном плане эквивалентен резистивному элементу с сопротивлением

 

,

при этом расчетная схема замещения для момента прихода волны к стыку линий имеет вид на рис. 7,б.

Так, если падающая волна напряжения имеет прямоугольную форму и величину , то в соответствии со схемой замещения на рис. 7,б напряжение на стыке линий в момент прихода волны

.

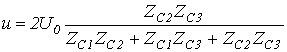Этой величине будут равны волны напряжения, которые пойдут далее в линии с волновыми сопротивлениями  и . Отраженная же волна, которая пойдет по линии с волновым сопротивлением , будет характеризоваться напряжением

.

Таким образом, по правилу удвоения волны определяются отраженные (появившиеся в результате отражения от неоднородности) и преломленные (прошедшие через неоднородность) волны, расчет которых осуществляется по схемам замещения с сосредоточенными параметрами. Следовательно, методика расчета переходных процессов в цепях с распределенными параметрами состоит в последовательном составлении схем замещения с сосредоточенными параметрами для каждого момента прихода очередной падающей волны на очередную неоднородность и расчете по ним отраженных и преломленных волн.

В качестве примера рассмотрим падение прямоугольной волны напряжения величиной  на включенный в конце линии конденсатор  (см. рис. 8,а).

Для расчета напряжения на конденсаторе и тока через него в момент прихода волны к концу линии составим схему замещения с сосредоточенными параметрами (см. рис. 8,б). Для этой схемы можно записать

,

где .

Это напряжение определяется суммой прямой (падающей) и обратной (отраженной) волн, т.е.

,

откуда для отраженной волны имеет место соотношение

или для той же волны в произвольной точке линии с координатой , отсчитываемой от конца линии, с учетом запаздывания на время  -

.

Соответственно для отраженной волны тока можно записать

.

Эпюры распределения напряжения и тока вдоль линии для момента времени , когда отраженная волна прошла некоторое расстояние , представлены на рис. 9. В этот момент напряжение на конденсаторе

и ток через него

.

В качестве другого примера рассмотрим падение прямоугольной волны напряжения величиной   на включенный в конце линии индуктивный элемент (см. рис. 10,а). В соответствии с расчетной схемой на рис. 10,б для тока через катушку индуктивности и напряжения на ней соответственно можно записать

;

,

где

С учетом этого выражения для отраженных волн напряжения и тока в произвольной точке линии имеют вид

;

.

Эпюры распределения напряжения и тока вдоль линии для момента времени  приведены на рис. 11.

 

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

2. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.

3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

1. Как расчет переходных процессов в длинных линиях сводится к нулевым начальным условиям?

2. В чем смысл правила удвоения волн, для чего оно используется?

3. Сформулируйте методику расчета переходных процессов в цепях с распределенными параметрами.

4. Что называется отраженными и преломленными волнами?

5. В линии на рис. 2 , , . Определить волны тока и напряжения, возникающие при коммутации, если .

Ответ: ; ; .

6. Рассмотреть падение волны напряжения, возникшей при коммутации в схеме предыдущей задачи, на резистор 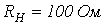 и определить обратные волны тока и напряжения, образующиеся при этом падении.

Ответ: ; .

7. К линии, находящейся под напряжением 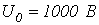, подключается незаряженная линия (см. рис. 12). Определить волны тока и напряжения, возникающие при этой коммутации, если , .

Ответ: ; ; .

8. Рассмотреть падение волны напряжения при коммутации в схеме предыдущей задачи на резистор  и определить возникающие при этом обратные волны напряжения и тока.

Ответ: ; .

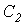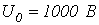9. Однородная длинная линия с  нагружена на емкостный элемент с . Посередине линии параллельно ему включен еще один конденсатор с . От генератора вдоль линии распространяется волна напряжения, которую до падения на конденсатор  можно считать прямоугольной с . Записать выражение для напряжения на конденсаторе .

Ответ: .