9.4/ Консервативная и диссипативная силы__

Потенциальное поле_

Поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного по­ложений.

Консервативные силы

Сила, работа которой при перемещении тела из одно­го положения в другое не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений тела (точки 1 и 2 на рисунке). Пример: сила тяжести.

Диссипативные силы_

Сила, работа которой зависит от траектории перемещения тела из одной точки в другую.

Пример: силы трения и сопротивления.

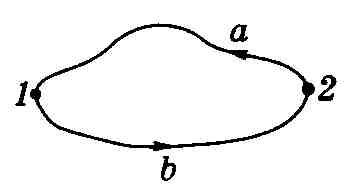Работа консервативных сил по замкнутому пути

•А⁼ А_1b2 + А_2а1 = 0 (работы А_1Ь2 и А_2а1 не зависят от траектории перемещения; они равны и отличаются только знаками).

Потенциальная энергия и консервативные силы__

Потенциальная энергия_

Механическая энергия системы тел, определяемая их взаимным распо­ложением и характером сил взаимодействия между ними.

Связь работы консервативных сил и потенциальной энергии

Работа консервативных сил не зависит от траектории и по любому замк­нутому пути равна нулю 9.4. Изменение потенциальной энергии, равное по величине работе, тоже не будет зависеть от траектории и по любому замкнутому пути будет равным нулю. Следовательно, запас потен­циальной энергии, как возможной работы консервативных сил, опре­деляется только начальной и конечной конфигурациями системы.

Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком «минус», так как работа совершается за счет убыли потенциальной энергии.

Характерные особенности потенциальной энергии

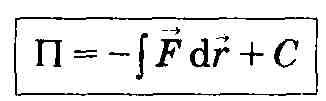
,(С — постоянная интегрирования).

Потенциальная энергия определяется с точностью до некоторой произ­вольной постоянной. Это, однако, не отражается на физических, зако­нах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потен­циальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.

Связь между консервативной силой и потенциальной энергией

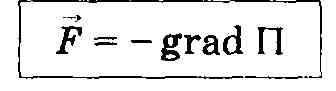
Для консервативных сил , или в векторном виде F = - grad П.

[— градиент скаляра П (i, j, k — единичные векторы координатных осей)]

Примеры вычислений потенциальной энергии. Полная энергия_

Конкретный вид функции П зависит от характера силового поля.

Потенциальная энергия тела массой т на высоте h

Это выражение вытекает из того, что потенциальная энергия равна работе силы тяжести при падении тела с высотыh на поверхность Земли.

Высота h отсчитывается от нулевого уровня, для которого П₀ = 0, g — ускорение свободного падения.

Поскольку начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энер­гию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина Л'), П = -mgh'.

Потенциальная энергия упруго деформированного тела (пружины)

Э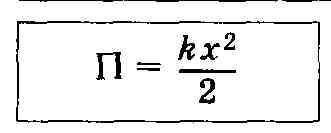то выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины.

Элементарная работа dA, совершаемая силой F_x при бесконечно малой деформации dx, dA = F_x dx = kx dx (F_x = -F _{x упр} = -(-kx) = kx).

Полная работа .

[k — коэффициент упругости (для пружины — жесткость); F_{х упр} =- kx - проекция силы упругости на ось х; F_{х упр} направлена в сторону, противопо­ложную деформации x. По третьему закону Ньютона деформирующая сила равна по модулю силе упругости и противоположно ей направлена]

Полная механическая энергия системы___Энергия механического движения и взаимодействия, т. е. равна сумме кинетической и потенциальной энергий.