8. Законы сохранения импульса Основные понятия_

Механическая система_

Совокупность материальных точек (тел), рассматриваемых как единое целое.

Внутренние силы

Силы взаимодействия между материальными точками механической системы.

Внешние силы

Силы, с которыми на материальные точки механической системы дейст­вуют внешние тела.

Замкнутая система_

Механическая система тел, на которую не действуют внешние силы.

Закон сохранения импульса

Исходные данные__

Рассматривается механическая система из п тел, масса и скорость кото­рых соответственно равны m₁ , m₂ , ... , m_n и .

Второй закон Ньютона для каждого из п тел механической системы_

[ — равнодействующие внутренних сил, действую­щих на каждое тело механической системы; — равно­действующие внешних сил, действующих на каждое тело механи­ческой системы]

После почленного сложения уравнений

П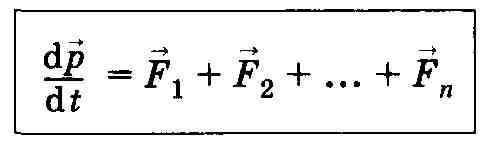роизводная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.

Здесь учли, что — импульс системы, а геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю.

В случае замкнутой системы

Внешние силы отсутствуют (или геометрическая сумма всех внешних сил равна нулю).

Закон сохранения импульса_

И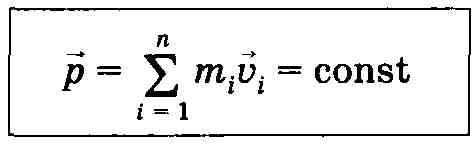мпульс замкнутой системы сохраняется, т. е. не изменяет­ся с течением времени.

Этот закон — фундаментальный закон природы (он универ­сален).

Закон сохранения импульса — следствие однородности пространства_

Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

♦ Импульс сохраняется и для незамкнутой системы, если геометрическая сумма внешних сил равна нулю.

8. Закон движения центра масс

Центр масс системы материальных точек (тела)_

Воображаемая точка С, положение которой характеризует распределе­ние массы этой системы (тела).

Для определения положения центра масс достаточно поочередно подве­сить тело за две различные точки на его поверхности и провести через точки подвеса вертикали, пересечение которых и даст положение центра масс (центр масс может располагаться вне тела).

Радиус-вектор центра масс_

[m_i и — соответственно масса и радиус-векторi-й материальной точки; п — число материальных точек в системе; — масса системы]

Скорость центра масс___

Учли, что =

Импульс системы материальных точек

Равен произведению массы системы на скорость ее центра массP_i = m_iv_i; p = Σp_t.

Закон движения центра масс

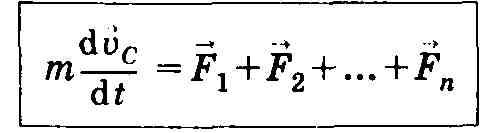Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе