6.4. Основной закон динамики для неинерциальных систем отсчета

Запись основного закона динамики для неинерциальных систем отсчета

Слагаемые в формуле основного закона
F = та		Сила, обусловленная воздействием тел друг на друга	1.25
		Сила инерции	1.26
Fц = -m·ω2R		Центробежная сила инерции	1.27
		Сила Кориолиса	1.28

Особенности сил инерции

• Силы инерции обусловлены не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона.

Силы инерции действуют только в неинерциальных системах отсчета.

Три возможных проявления сил инерции_

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил:

• Силы инерции при ускоренном поступательном движении системы отсчета.

• Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета.

• Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.

• 7 ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ

• 7,1. Преобразования координат Галилея

• Исходные данные

• Рассматривают две системы отсчета: инерциальную сис­тему отсчета К (с координатами х, у, z), условно считая ее неподвижной, и систему К' (с координатами х', у', z'), движущуюся относительно К равномерно и прямоли­нейно со скоростью ( = const). Отсчет времени — с мо­мента, когда начала координат обеих систем совпадают. На рисунке показано расположение систем в произволь­ный момент времени t. Скорость направлена вдоль ОО'; .

• Преобразования координат Галилея

• • 

  Задают связь между радиусами-векторами или координатами произвольной точки А в обеих системах.

• Частный случай преобразований Галилея

• • x' = x - vt,

  • y' = y,

  • z' = z

  Система К' движется со скоростью вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают).

• В классической механике считается, что ход времени не зависит от отно­сительного движения сиcтем отсчета, т. е. к преобразованиям Галилея добавляют уравнение t' = t.

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ

Формулировки принципа относительности Галилея

Законы динамики одинаковы во всех инерциальных системах отсчета.

• Все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу.

• Правило сложения скоростей в классической механике

• 

• Продифференцировав по времени и учитывая, чтоt' = t , ,

• получим .

• [ — скорость движения системы К' относительно системы К; и — со­ ответственно скорости в системах К и К']

• Подтверждение принципа относительности Галилея

• (механического принципа относительности)__

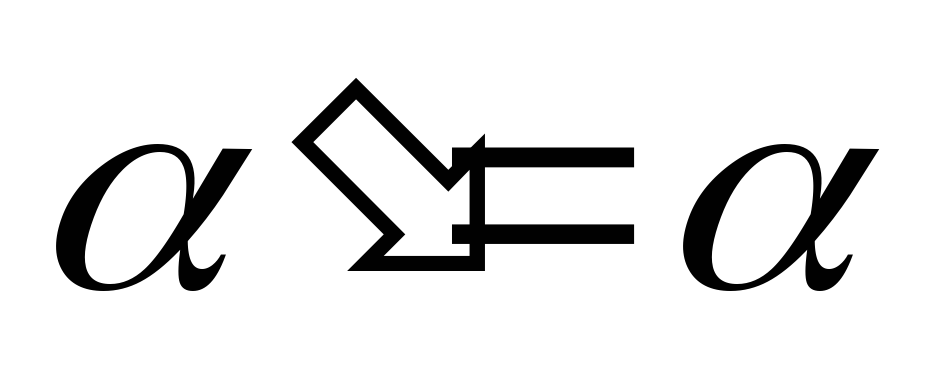• В системе К ускорение . Следовательно, если на точку А другие тела не действуют (= 0), тоа' = 0, т. е. системаК' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).

• Из равенства а' = а вытекает подтверждение принципа относительности Галилея (механического принципа относительности): уравнения дина­мики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. являются инвариантными по отношению к преобразованиям координат.

• Никакими механическими опытами, проводимыми внутри данной инер­циальной системы отсчета, нельзя установить, покоится она или движет­ся равномерно и прямолинейно. Во всех инерциальных системах отсчета одинаковы свойства пространства и времени, одинаковы и все законы механики.