1.67 Работа в гравитационном поле______________________________________________

Работа по перемещению тела массойт в поле тяготения на расстояние dR

Знак минус появляется потому, что силаи перемещение противоположны по направлению.

Работа при перемещении с расстояния R₁ до R₂ ___________________________________________________________

[М — масса Земли]

Вывод. Затраченная работа в гравитационном поле не зависит от траекто­рии перемещения, а определяется лишь начальным и конечным положе­ниями тела, т. е.силы тяготения консервативны, аполе тяготения является потенциальным 1.38.

1.68 Потенциал гравитационного поля____________________________________________________

Потенциальная энергия тела массой т в гравитационном поле______________________________________

Работа, совершаемая консервативными силами, равна изменению по­тенциальной энергии системы, взятому со знаком минус1.39: А = - ΔП = - (П₂– П₁) = П₁- П₂. Тогда, учитывая выражение для А 1.67, имеем П₁- П₂=-m(GM/R₁-GM/R₂.). ПриR₂ → ∞ потенциальная энергия П₂→ 0. Первая точка выбрана произвольно, получаем записанное выра­жение.

[G — гравитационная постоянная; М — масса Земли; R — радиус Земли]

Потенциал гравитационного поля________________________________________________________________

Физическая величина, определяемая потенциальной энергией тела еди­ничной массы в данной точке поля или работой по перемещению единич­ной массы из данной точки поля в бесконечность.

Потенциал гравитационного поля — энергетическая скалярная харак­теристика.

Единица потенциала гравитационного поля__________________________________________________________________

1джоуль на килограмм (Дж/кг) — потенциал такой точки гравитацион­ного поля, в которой тело массой 1 кг обладает потенциальной энергией 1Дж.

Потенциал поля тяготения, создаваемого телом массой М

[G — гравитационная постоянная; R — расстояние от этого тела до рассматривае­мой точки]

46

Потенциальная энергия тела на высоте h относительно Земли

Исходя из представлений теории тяготения, GmM ( GmM) _ GmMh

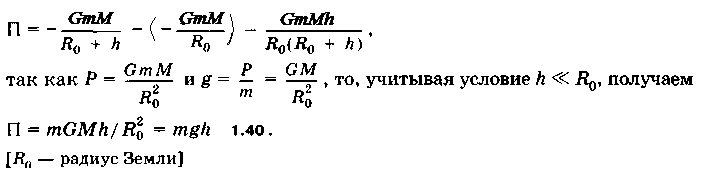
1.69 Напряженность как градиент потенциала_____________________________________________

Связь между напряженностью и потенциалом гравитационного поля_________________________________

При перемещении тела массойт в поле тяготения Земли на расстояние dR совершается работа

Тогда Учитывая, что, получаемmg dl=mdφили

Величинaхарактеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения.

g.

Знак минус указывает, что вектор напряженности g направленв сторону убывания потенциала

— градиент скаляра φ

Эквипотенциальные поверхности________________________________________________________________

Поверхности, во всех точках которых потенциал φ гравитационного поля имеет одно и то же значение.

Предназначение:для графического изображения распределения потенциала.

1.70 Космические скорости

Космические скорости_____________________________________________________________________________________

Скорости для достижения определенных космических орбит.

Первая космическая скорость_______________________________________________________________________________

Минимальная скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т. е. превратиться в искусственный спутник Земли.

На спутник, движущийся по круговой орбите радиусом r, действует сила тяготения Земли, сообщающая ему нормальное ускорение V₁²/r. По второму закону Ньютона GmM/г² = m V₁²/r. Если спутник движется вблизи поверхности Земли, в этом случае г ≈ R₀ (радиус Земли) и g = GmM /R ₀² 1.68, то у поверхности Земли = 7,9 км/с.

Вторая космическая скорость_______________________________________________________________________________

Наименьшая скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической.

47

Чтобы тело (при отсутствии сопротивления среды) могло преодо­леть земное притяжение и уйти в космическое пространство, его кинетическая энергия должна быть равна работе, совершаемой против сил тяготения:

,

откуда

Третья космическая скорость_______________________________________________________________________________

Скорость, которую необходимо сообщить телу на Земле, чтобы оно по­кинуло пределы Солнечной системы, преодолев притяжение Солнца. [g — ускорение свободного падения; R_n — радиус Земли; G — гравитационная постоянная; m — масса тела; М — масса Земли]