1.5. Тяготение. Элементы теории поля

1.5.1. Законы кеплера. Закон всемирного тяготения

1.61 Три закона Кеплера_______________________________________________________________

Первый закон Кеплера____________________________________________________________________________________

Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

Отметим тщательный анализ показал, что в одном из фокусов находится не центр Солнца, а центр масс системы Солнце — планета.

Перигелий____________________________________________________________________________________________

Ближайшая к Солнцу точка орбиты небесного тела, вращающегося во­круг него.

Расстояние в перигелии между центрами Земли и Солнца составляет 1,47·10⁸км.

Афелий________________________________________________________________________________________________

Наиболее удаленная от Солнца точка орбиты небесного тела, вращаю­щегося вокруг него.

Второй закон Кеплера__________________________________________________________________________________

Если начало координат расположено в центре масс Солнца, то радиус-вектор планеты за равные промежутки времени описывает одинаковые пло­щади.

Третий закон Кеплера ______________________________________________________________________________

К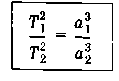вадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Третий закон Кеплера в применении к планетам и спутникам позволяет, в частности, подсчитать массы планет.

Закон всемирного тяготения

Формулировка закона всемирного тяготения__

М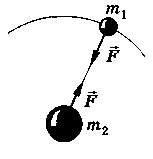ежду любыми двумя телами (материальными точками) действует сила взаимного притяжения, прямо пропорциональная произведению масс этих тел{т₁ и т₂) и обратно пропорциональная квадрату расстояния (г) между ними.

[G = 6,67 • 10 ⁿ Н • м²/кг² — гравитационная по­стоянная; F — сила тяготения]

♦ Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через центры масс взаимодействующих тел.

Закон всемирного тяготения открыт Ньютоном при изучении движения небес­ных тел на основе законов Кеплера и основных законов динамики.

Определение гравитационной постоянной

Принципиальная схема опыта Кавендиша с применением крутильных весов

Легкое коромысло А с двумя одинаковыми шарика­ми массой т = 729 г подвешено на упругой нити. На коромысле В укреплены на той же высоте массивные шары массой М — 158 кг. Поворачивая коромысло В вокруг вертикальной оси, можно изменять расстоя­ние между шарами с массами т и М. Под действием пары сил, приложенных к шарам т со стороны ша­ров М, коромысло А поворачивается в горизонталь­ной плоскости, закручивая нить до тех пор, пока момент сил упругости не уравновесит момент сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяже­ния, а так как массы шаров известны, то и вычислить значение G.

♦ Согласно закону всемирного тяготения 1.62 и вычисленному значению G (G = 6,67 • 10 ^-11 Н • м²/кг²), два точечных тела массой по 1кг каждое, находя­щиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,67 · 10 ^-11 Н. Это означает, что сила гравитационного взаимодействия значительна только в случае больших масс.