1.56 Закон сохранения момента импульса________________________________________________

Еще одна форма записи

уравнения динамики вращательного движения твердого тела__________________________________________________

Производная момента импульса твердого тела относительно оси равна моменту силы относительно той же оси.

Продифференцировав L_z = J_zm 1.55по времени, получим записанное выражение:

Производная вектора момента импульса твердого тела равна моменту (сумме моментов) внешних сил.

Закон сохранения момента импульса________________________________________________________________________

Момент импульсазамкнутой системы сохраняется, т.е. не изменяется с течением времени.

В замкнутой системе момент внешних сил и, откуда

♦ Закон сохранения момента импульса – фундаментальный закон природы.

Закон сохранения момента импульса – следствие изотропности пространства____________________________________

Изотропность пространства — инвариантность физических законов относительно выбора направления осей координат системы отсчета (от­носительно поворота замкнутой системы в пространстве на любой угол).

Некоторые демонстрации закона сохранения момента импульса________________________________________________

Человек, сидящий на скамье Жуковского (она с малым трением враща­ется вокруг вертикальной оси) и держащий в вытянутых руках гантели, приведен во вращение с угловой скоростью ω₁. Если человек прижмет ган­тели к себе, то момент инерции системы уменьшится. Поскольку момент

внешних сил равен нулю, момент импульса системы сохраняется (J^Oj) = с/₂^ш2)^иугло­вая скорость вращения <м₂возрастает.

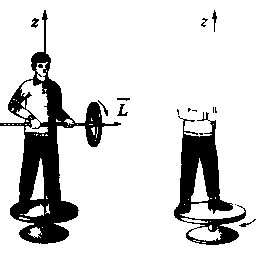Человек, стоящий на скамье Жуковского (она с малым трением вращается вокруг вертикальной оси), держит в руках колесо, вращающееся вокруг горизонтальной оси. Начальный момент импульсаЬ_г = 0. Если поднять вращающееся колесо (правый рису­нок), тоЬ_г остается равным нулю (поворот колеса осуществляется за счет внутренних сил) и скамья начнет вращаться в направ­лении, противоположном направлению вра­щения колеса с угловой скоростью со₂, удов­летворяющей равенствуЬ_г =J₁(H₁ - J-^-z ⁼0 (Jj— момент инерции колеса;a»j— угловая скорость колеса;J₂ — момент инерции сис­темы «человек + скамья»).

Гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увели­чить тем самым угловую скорость вращения.

1.57 Аналогия в описании

поступательного и вращательного движений______________________________________

Поступательное движение		Вращательное движение
Масса	т	Момент инерции	J
Скорость		Угловая скорость	d<5 dt
Ускорение		Угловое ускорение	dto E=dJ
Сила		Момент силы	Мгили М
Импульс		Момент импульса	Ьг = J2m
Основное уравнение динамики		Основное уравнение динамики	M = — dt
Работа	dA = F, ds	Работа	dA = Mг d(p
Кинетическая энергия	mv2 2	Кинетическая энергия	Jza2
			2

1.4.4. ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА 1.58 Виды деформаций_________________________________________________________________

Деформация

Изменение формы и размеров твердых Упругая деформация тел под действием внешних сил.

Деформация, исчезающая с прекращением действия внешних сил.

40

Пластическая (остаточная) деформация__________________________________________________________________________

Деформации, сохраняющиеся в теле после прекращения действия внеш­них сил.

Деформации реального тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь.

Относительная деформация_______________________________________________________________________

Количественная мера, характеризующая степень деформации и определяемая отношением абсолютной деформации Δх к величинех (характе­ризует первоначальные размеры и форму тела).

Относительная продольная деформация___________________________________________________________

Относительное изменение длины стержня.

К концам стержня длиной l приложены направленные вдоль его оси равные силы F, в результате чего длина стержня изменяется на величину Δl.

При растяжении Δl положительно, а при сжатии отрица­тельно.

Относительное поперечное растяжение (сжатие)______________________________________________________________

Относительное изменение диаметра стержня.

ε и ε' всегда имеют разные знаки (при растяжении Δl положительно, a Δd отрицательно, при сжатии Δl отрицательно, a Δd положительно).