10.3. Момент силы. Основное уравнение динамики вращательного движения

Момент силы

Момент силы относительно неподвижной точки О

Физическая величина, определяемая векторным произведением радиуса-вектора, проведенного из точки О в точку А приложения силы, на силу .

- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль вектора момента силы_

[а— угол между и; — кратчайшее расстояние между линией действия силы и точ­кой О - плечо силы]

Момент силы относительно неподвижной оси

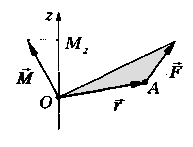
Скалярная величина М_г, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z/ Значение момента М_z не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора , то момент силы представляется в виде вектора, совпадающего с осью.

Уравнение динамики вращательного движения твердого тела

Исходные данные для вычисления работы при вращении тела

Сила приложена к точке В, находящейся от оси на расстоянии r, α — угол между направлением силы и радиусом-вектором . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.

Работа при вращении тела__

При повороте тела на бесконечно малый угол dφ точка В силы проходит путь rdφ и работа равна произведению проекции силы на направление смещения на величину смещения: d А = F sin α·r·dφ. Учитывая, что М_z = F·r· sin α = F·l 1.53, получаем dA = М_г dφ.

Уравнение динамики вращательного движения твердого тела____________________________________________________

Момент сил твердого тела относительно оси равен произведению момента инерции относительно той же оси на угловое ускорение.

Работа вращения тела идет на увеличение его кинетической энергии:

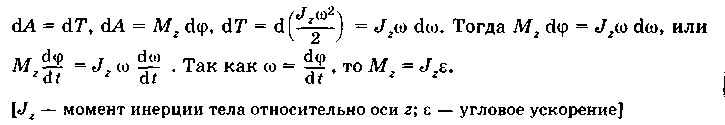
1.4.3. Момент импульса и закон его сохранения

1.55 Момент импульса____________________________________________________________________________________

Момент импульса материальной точки относительно неподвижной точки О______________________________________

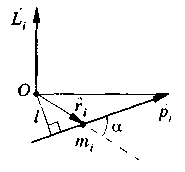Физическая величина, определяемая векторным произведением радиус-вектора, материальной точки, проведен­ного из точкиО, на импульс , этой матери­альной точки.

—псевдовектор, его направление совпадает с направлением поступательного движения право­го винта при его вращении от , к

Модуль вектора момента импульса__________________________________________________________________________

[a — угол между векторами г, и Д.; / = г sin a — плечо импульса. Перпендикуляр опущен из точки О на пря­мую, вдоль которой направлен импульс частицы]

Момент импульса материальной точки относительно

неподвижной оси z_________________________________________________________________________________________

Скалярная величина L_iz, равная проекции на эту ось вектора момента импульса, определенного от­носительно произвольной точки О данной оси г.

Значение момента импульса L_u не зависит от по­ложения точки О на оси г.

38

Момент импульса отдельной точки вращающегося абсолютно твердого тела_____________________________________

При вращении абсолютно твердого тела вокруг неподвижной осиг каждая отдельная точка тела движется по окружности постоянного радиуса г, с некоторой скоростью v_r Скорость v_t и импульс m_jv_i пер­пендикулярны этому радиусу, т. е. радиус — плечо вектора mfi_r Тогда момент импульса отдельной частицы L_jz = m_jv_jr_j и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса абсолютно твердого тела относительно неподвижной оси z____________________________________

С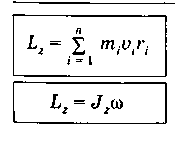умма моментов импульса отдельных его частиц относительно той же оси.

Равен произведению момента инерции тела относительно той же оси на угловую скорость.

(учли, что ).

[J₂ — момент инерции тела относительно оси z; ω — угловая скорость]