10. Динамика вращательного движения

10.1. Момент инерции.

Определение момента инерции

Момент инерции тела относительно неподвижной оси_

Физическая величина, равная сумме про­изведений элементарных масс на квадра­ты их расстояний до рассматриваемой оси. Суммирование производится по всем эле­ментарным массамт_i на которые можно разбить тело.

Момент инерции - величина аддитивная: момент инерции тела равен сумме моментов инерции его частей.

Момент инерции тела в случае непрерывного распределения масс

Интегралы берутся по всему объему тела, причем величины p и r являются функциями точки (например, декартовых ко­ординат x, y и z).

[p- плотность тела в данной точке; dm = р dV - масса малого элемента тела объемом dV, отстоящего относительно оси вращения на расстоянии r;]

Момент инерции сплошного цилиндра. Теорема Штейнера__

Момент инерции однородного сплошного цилиндра радиуса R относительно его геометрической оси__

Разобьем цилиндр на отдельные полые концент­рические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним (r + dr). Момент инерции каждого полого цилиндра dJ = r² dm (dr << r), объем элементарного цилиндра 2πrh· dr, его масса dm = 2πrhp· dr и dJ = 2πhpr³· dr (p — плотность материала). Момент инерции сплошного цилиндра

.

Поскольку πR²h - объем цилиндра, его масса т = πR²hp, а .

Теорема Штейнера

J = J_C+ та² Момент инерции тела J относительно любой оси вращения равен моменту его инерции J_с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями.

1.51 Моменты инерции однородных тел

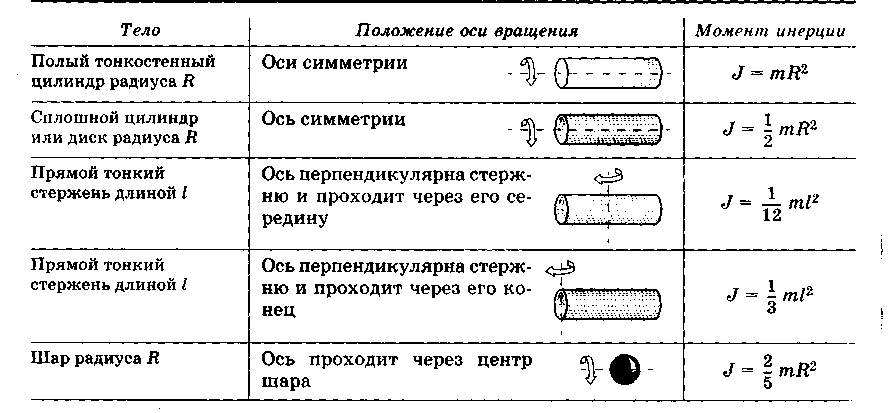
10.2. Кинетическая энергия вращающегося твердого теланые

Исходные данные. Тело вращается вокруг неподвижной оси z. Мысленно разбиваем это тело на элементарные массы m₁, т₂, ... , m_i, ... , находящиеся от оси на расстояниях r₁, r₂, ... , r_i, ... . При вращении твердого тела элементарные объемы массами m_i, опишут окружнос­ти различных радиусов r_i.

Кинетическая энергия i-й элементарной массы

Линейная скорость элементарной массы v_it = wr_i- (угловая скорость вращения всех элементарных объемов одинакова).

Кинетическая энергия вращающегося твердого тела

(учли, что );J_z – момент инерции тела относительно оси z.

Из сравнения формул иследует, чтомомент инерции - мера инертности тела при вращательном движении.

Кинетическая энергия тела при плоском движении

Складывается из энергии поступательного движения со скоро­стью, равной скорости центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела.

[т - масса тела; V_C - скорость центра масс тела; J_C- момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела]