9.6.. Удар абсолютно упругих и неупругих тел

Общие понятия_______________

Удар (соударение)_____

Примеры: столкновение бильярдных шаров, удар человека о землю при прыжке с поезда и т.д.

. Столкновение двух или более тел, при котором взаимодействие длится очень короткое время.

Система тел в процессе соударения — замкнутая система

Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процессе их со­ударения приближенно рассматривать как замкнутую систему и при­менять к ней законы сохранения.

Сущность удара__

Кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.

Коэффициент восстановления___

Отношениенормальных составляющих относительной скорости тел пос­ле ()и до (V_n) удара.

Такие тела — абсолютно неупругие.

Такие тела — абсолютно упругие .

Примеры: для стальных шаров ε ≈ 0,56; для слоновой кости ε ≈ 0,89; для свинца ε ≈ 0.

Линия удара_

Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.

Центральный удар__

Удар, при котором тела до удара движутся вдоль прямой, проходящей через их центры масс.

Центральный абсолютно упругий удар

Абсолютно упругий удар_

Столкновение двух тел, в результате которого в обоих взаимодействую­щих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кине­тическую энергию.

Следует отметить, что это идеализация.

Исходные данные_

Сталкиваются шары массами т₁ и т₂; скорости шаров до удара — v₁ и v₂, после удара — v{ и v'₂. В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учитываются знаками: положительное зна­чение приписывается движению вправо, отрицательное — движению влево. Выполняются законы сохранения импульса и энергии.

Законы сохранения импульса и механической энергии______

Эти законы записаны при сделанных выше допуще­ниях.

Скорости тел после абсолютно упругого удара

После преобразования законов сохранения

; (*)

; (**)

.

Решая (*) и (**), получим записанные выражения.

Частные случаи

Шары с одинаковыми массами

и\ = v₂ ;

V₂ = Uj.

Шары равной массы «обмениваются» энергией. окоится

г ..

Если второй шар до удара висел неподвижно (v₂ = 0), то после удара остановится первый шар ( v\ = 0), а второй будет двигаться с той же скоро­стью и в том же направлении, в котором двигался первый шар до удара ( v'₂ = i^).

Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (v\ < i>j). Скорость второго шара после удара больше, чем скорость первого после удара ( V₂ > v\).

Направление движения первого шара при ударе изменяется — шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигал­ся первый шар до удара, но с меньшей скоростью,

т. е. и о < v

Пример: столкновение шара со стеной:

Центральный абсолютно неупругий удар

Абсолютно неупругий удар___________

Столкновение двух тел, в результате которого тела объединяются, двига­ясь дальше какединое целое.

Пример: шары из пластилина, движущиеся навстречу друг другу.

Исходные данные___

Сталкиваются шары массами m₁, и m₂; скорости шаров до удара — и ; — общая скорость шаров после удара.

Общая скорость шаров после удар

Вычисляется, согласно закону сохранения импульса:

.

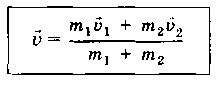
Движение шаров навстречу друг другу__

Шары будут продолжать двигаться вместе в ту сто­рону, в которую двигался шар, обладающий боль­шим импульсом.

О законе сохранения механической энергии_

В процессе центрального абсолютно неупругого удара шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, поэтому эти силы подобны силам трения и закон сохранения механической энергии не соблюдается. Вследствие деформации происходит «по­теря» кинетической энергии, перешедшей в тепловую или другие формы энергии.

Разность кинетических энергий тел до и после абсолютно неупругого удара_

Учли выражение для V.

Случай V₂ = 0 (ударяемое тело первоначально неподвижно)

Если т₂ >> т₁ (масса неподвижного тела очень большая), то V << V₁ и почти вся кинетическая энергия при ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молота.