Динамика

один из основных разделов механики.

Динамика изучает законы движения материальных точек (тел) и причины, это движение вызывающие. При cкорости движения v << c ( c = 3 ·10⁸ м/с – скорость света в вакууме) действуют законы классической (ньютоновской, нерелятивистской) механики; если же v ~ c – законы релятивистской (эйнштейновской) механики.

Основы динамики поступательного движения

1. ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА. МАССА ЗАКОНЫ НЬЮТОНА. ИМПУЛЬС ТЕЛА. СИЛА

1. 1.1. ПЕРВЫЙ ЗАКОН НЬЮТОНА_

2. _______________________________________________________________

ФОРМУЛИРОВКИ ПЕРВОГО ЗАКОНА НЬЮТОНА

Всякая материальная точка (тело) сохраняет состояние покоя или равно­мерного прямолинейного движения до тех пор, пока воздействие со сто­роны других тел не заставит ее изменить это состояние. (В этой формули­ровке Ньютон привел закон, установленный еще Галилеем.)

Существуют такие системы отсчета, относительно которых поступатель­но движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела (или действие других тел компенсируется).

Утверждение о существовании инерциальных систем отсчета составляет содержание первого закона Ньютона.

Инерциальная система отсчета

Система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.

Неинерциальная система отсчета

Система отсчета, движущаяся относительно инерциальной системы от­счета с ускорением.

Инерциальность гелиоцентрической системы отсчета_

Опытным путем установлено, что инерциальной можно считать гелио­центрическую (звездную) систему отсчета (начало координат находит­ся в центре Солнца, а оси проведены в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальная, одна­ко эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач пренебрежимо малы, и в этих случаях ее можно считать инерциальной.

1.2 МАССА И ИМПУЛЬС ТЕЛА. СИЛА

ИНЕРТНОСТЬ ТЕЛ

Свойство, присущее всем телам и заключающееся в том, что тела оказы­вают сопротивление изменению его скорости (как по модулю, так и по направлению).

Масса тела

Физическая величина, являющаяся одной из основных характеристик ма­терии, определяющая ее инерционные (инертная масса) и гравитацион­ные (гравитационная масса) свойства.

В настоящее время можно считать доказанным, что инертная и гравита­ционная массы равны друг другу (с точностью, не меньшей 10~¹² их зна­чения).

Свойства массы в рамках классической механики

Масса — величина аддитивная (масса составного тела равна сумме масс его частей); величина постоянная (не изменяется при движении тела).

Единица измерения массы

1 килограмм — масса, равная массе международного прототипа килограмма (платиново-иридиевого цилиндра, хранящегося в Международном бюро мер и весов).

1.3. ИМПУЛЬС МАТЕРИАЛЬНОЙ ТОЧКИ (ТЕЛА)

Векторная величина, численно равная произведению массы материаль­ной точки (тела) на ее скорость и имеющая направление скорости.

Единица измерения импульса

1 килограмм-метр в секунду равен импульсу материальной точки (тела) массой 1 кг, движущейся со скоростью 1 м/с.

1.4.СИЛА

Векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приоб­ретает ускорение или изменяет свою форму и размеры.

В каждый момент времени сила характеризуется числовым значением, направлением в

пространстве и точкой приложения.

4. ВТОРОЙ ЗАКОНЫ НЬЮТОНА

является основным законом динамики поступательного движения.

41.Общая формулировка второго закона Ньютона

Скорость изменения импульса материальной точки (тела) равна дейст­вующей на нее (него) силе.

Записанное уравнение называют еще уравнением движения материаль­ной точки.

4.2.Еще одна формулировка второго закона Ньютона

или

Ускорение, приобретаемое материальной точкой (телом), пропорцио­нально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

Единица силы 1 Н = 1 (кг • м)/с²

1 ньютон — сила, которая массе в 1 кг сообщает ускорение 1м/с² в направлении действия силы.

♦ Второй закон Ньютона справедлив только в инерциальных системах отсчета .

1.44.3. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ

Формулировка принципа независимости действия сил

Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.

Ускорение, приобретаемое точкой под действием нескольких сил

-результирующая сила. Силаможет быть разложена на две составляющие —тангенциальную () и нор­мальную

(см. рисунок).

Тангенциальная и нормальная составляющие силы

Разложение силы на составляющие приво­дит к существенному упрощению решения задач. Например, на рисунке действующая силаF = та разложена на два компонента: тангенциальную силу F_T (направлена по касательной к траектории) и нормальную силу F_n (направлена по нормали к центру кривизны).

♦ Если на материальную точку действует одновременно несколько

сил, то, со­гласно принципу независимости действия сил, под F

во втором законе Ньютона понимают результирующую силу.

4.5.СИЛЫ В МЕХАНИКЕ

СИЛА ТЯГОТЕНИЯ (СИЛА ГРАВИТАЦИОННОГО ВЗАИМОДЕЙСТВИЯ )

Закон всемирного тяготения

Формулировка закона всемирного тяготения__

Между любыми двумя телами (материальными точками) действует сила взаимного притяжения, илисила гравитационного взаимодействия, прямо пропорциональная произведению масс этих тел {т₁ и т₂) и обратно пропорциональная квадрату расстояния (г) между ними.

[G = 6,67 • 10 ⁿ Н • м²/кг^{2 -} гравитационная по­стоянная; F — сила тяготения] .

♦ Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через центры масс взаимодействующих тел.

Закон всемирного тяготения открыт Ньютоном при изучении движения небес­ных тел на основе законов Кеплера и основных законов динамики.

Определение гравитационной постоянной

Принципиальная схема опыта Кавендиша с применением крутильных весов

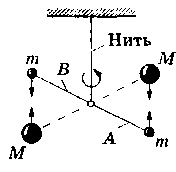Легкое коромысло А с двумя одинаковыми шарика­ми массой т = 729 г подвешено на упругой нити. На коромысле В укреплены на той же высоте массивные шары массой М — 158 кг. Поворачивая коромысло В вокруг вертикальной оси, можно изменять расстоя­ние между шарами с массами т и М. Под действием пары сил, приложенных к шарам т со стороны ша­ров М, коромысло А поворачивается в горизонталь­ной плоскости, закручивая нить до тех пор, пока момент сил упругости не уравновесит момент сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяже­ния, а так как массы шаров известны, то и вычислить значение G.

♦ Согласно закону всемирного тяготения 1.62 и вычисленному значению G (G = 6,67 • 10 ^-11 Н • м²/кг²), два точечных тела массой по 1кг каждое, находя­щиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,67 · 10 ^-11 Н. Это означает, что сила гравитационного взаимодействия значительна только в случае больших масс.