Моделирование случайной величины и

исследование ее распределения

Теоретические сведения

Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и‚ на первый взгляд‚ беспорядочно. Результат каждого отдельного измерения случайной величины практически непредсказуем. Однако совокупности результатов измерений подчиняются статистическим закономерностям, изучение которых служит одной из основ теории и практики физического и инженерного эксперимента. Существует множество законов распределения случайных величин. Одним из наиболее распространенных является нормальный закон распределения, описываемый функцией Гаусса:

. (1)

Закономерность распределения значений изучаемой случайной величины t становится наглядным, если построить гистограмму – ступенчатую диаграмму, показывающую, как часто при измерениях появляются значения, попадающие в тот или иной из равных интервалов Dt, лежащих между наименьшим и наибольшим из наблюдаемых значений величины t. Гистограмму строят в следующих координатах (рис. 1): ось абсцисс – измеряемая величина t; ось ординат – DN/(NDt). Здесь N – полное число наблюдений, DN – число результатов, попавших в интервал [t, t+Dt]. Частное DN/N – есть доля результатов, попавших в указанный интервал, и характеризует вероятность попадания в него результата отдельного наблюдения. Отношение этой величины к ширине интервала DN/(NDt) называется "плотностью вероятности".

При очень большом числе наблюдений () вместо ступенчатой гистограммы получается плавная кривая зависимости от t функции

Рис. 1

. (2)

Эту функцию называют плотностью вероятности или законом распределения по t. Чтобы сравнить наблюдаемое распределение с нормальным (1), нужно найти по данным наблюдений параметры <t> и s функции Гаусса (приближенно, поскольку число наблюдений ограничено). Параметр <t> есть среднее арифметическое случайной величины

. (3)

Параметр s является средним квадратичным отклонением наблюдений от среднего <t>:

. (4)

Из формулы (1) следует, что плотность нормального распределения имеет максимум при

, (5)

и симметрична относительно <t>. Нетрудно сравнить “наибольшую высоту гистограммы” и максимальное значение функции Гаусса (5). Для количественной проверки того, насколько хорошо полученные результаты соответствуют нормальному распределению, можно воспользоваться соотношением 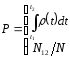(6),

, (6)

в котором вероятность Р₁₂ попадания результата измерения в интервал (t₁, t₂) c одной стороны может быть вычислено как интеграл функции Гаусса в этих пределах, а с другой стороны – найдена как относительное число наблюдений N₁₂ , результаты которых попали в этот интервал. При сравнении можно воспользоваться известными значениями вероятности распределения случайной величины для наиболее употребительного в технике измерений пределов:

t(<t>-s; <t>+s), Ps=0,68,

t(<t>-2s; <t>+2s), P₂s=0,95,

t(<t>-3s; <t>+3s), P₃s=0,997. (7)

Измерения и обработка результатов

Задание №1

Цель работы: исследовать распределение случайной величины.

Оборудование: электронный секундомер, часы.

В данной работе моделирование случайной величины осуществляется следующим образом. При помощи обычных часов с секундной стрелкой задают некоторый промежуток времени t и измеряют его высокочувствительным цифровым частотомером или электрическим секундомером, вручную нажимая кнопки "старт" и "стоп". Выполнять работу рекомендуется двум студентам. Первый многократно задает определенные промежутки времени по часам, подавая команду "старт" и "стоп". Второй нажимает кнопки и записывает отсчеты по прибору. В этом случае результаты измерений будут независимыми, что должно привести к нормальному (гауссовому) распределению случайной величины.

1. Проведите 50 раз измерение выбранного промежутка времени. Можно задать промежуток времени от 5 до 10 секунд. Показания цифрового частотомера занесите в табл.1.

2. Найдите в табл.1 наименьший t_min и наибольший t_max из результатов наблюдений. Промежуток (t_min–t_max) разбейте на 6–10 равных интервалов Dt. Границы интервалов желательно округлять таким образом, чтобы цифра последнего разряда имела значения 0, 2 или 5, а интервал Dt был кратен 2 или 5. Границы интервалов занесите в таблицу 2.

3. Подсчитайте число результатов наблюдений в табл. 2, попавших в каждый интервал Dt_i, и заполните второй столбец табл. 2.

4. Вычислите опытные значения плотности вероятности попадания случайной величины в каждый из интервалов Dt_i. Заполните третий столбец табл. 2.

5. Постройте гистограмму (рис. 1), для чего по оси абсцисс откладывайте интервалы Dt_i, являющиеся основаниями прямоугольников, высота которых равна плотности вероятности r_i.

6. Вычислите <t>, по (3) и s по (4) (здесь для экономии времени рекомендуется воспользоваться инженерным калькулятором). Можно воспользоваться результатами двадцати наблюдений. Полученные значения занесите в табл. 1.

7. По формуле (5) найдите максимальное значение плотности вероятности r_max при t=<t>. Результаты занести в табл. 1. Сравнить полученные значения r_max с наибольшей высотой гистограммы.

8. Для значений t, соответствующих границам выбранных интервалов, вычислите по функции Гаусса (1) значения плотности вероятности r(t) и занесите их в четвертый столбец табл. 2.

9. Нанесите все расчетные точки на график, на котором изображена гистограмма, и проведите через них плавную кривую. Сравните их. В чем причина неполного соответствия кривой Гаусса и гистограммы?

10. Проверьте, на сколько точно выполняется в опытах соотношение (7). Вычислите границы интервалов, указанных в первом столбце табл. 3. По данным табл. 1 подсчитайте число наблюдений N₁₂, попадающих в каждый из трех интервалов, а также отношение N₁₂/N. Сравните их с известными значениями Р₁₂, соответствующими нормальному распределению случайных величин (7). В чем причина небольшого расхождения?

Таблица 1

№ опыта	ti , c	№ опыта	ti , c	№ опыта	ti , c	№ опыта		ti , c	№ опыта	ti , c
1		11		21		31			41
2		12		22		32			42
.		.		.		.			.
10		20		30		40			50
<t> = ... , c		s= ... , c					rmax = ... , c-1

Таблица 2

Границы интервалов, с		с-1	r, с-1

Таблица 3

	Интервал, с		N12		N12/N		P12
	от	до
<t> ± s
<t> ± 2s
<t> ± 3s

Задание №2

Цель работы: определение абсолютной ошибки, накапливающейся в результате нескольких измерений.

Оборудование и материалы: электронные или рычажные весы, набор грузиков.

Каждое измерение вносит свой вклад в погрешность, что приводит к увеличению абсолютной ошибки, но, в силу случайного характера распределения отклонения от истинного значения, абсолютная ошибка не будет увеличиваться линейно с ростом количества измерений. Погрешность измерения будет определяться следующей формулой:

, (8)

здесь – аппаратурная погрешность. Если используется один прибор или приборы одного класса точности и значения друг от друга значительно не отличаются, то значение будет одинаково для всех измерений и формулу (8) можно переписать в виде

, (9)

N – количество измерений.

В данном задании, предлагается взвесить по отдельности N грузиков (N=25–50, предпочтительнее N=25, 36, 49). В качестве грузиков можно использовать любые мелки предметы, массой от 1 грамма до 15 грамм, например металлические монеты или кусочки пластилина. Вычислить общую массу грузиков , сложив полученные результаты. Вычислить по формуле (9) абсолютную погрешность данных измерений . Определить общую массу грузиков M, положив их на весы все сразу. Записать результаты измерений, расчетов и аппаратурную погрешность весов в таблицу №4.

Таблица 4

№ опыта	, г	№ опыта		, г	№ опыта		, г	№ опыта		, г
1		11			21			31
2		12			22			32
.		.			.			.
10		20			30			40
M = ... , г			= … , г			= … , г			= … , г

Записать полученные результаты в виде

,

,

объяснить полученные результаты.

Контрольное задание

При обработке результатов измерения емкости для партии конденсаторов получено <C>=1,1 мкФ, s=0,1 мкФ. Если взять коробку со 100 конденсаторами из этой партии, то сколько серди них можно ожидать конденсаторов с емкостью меньше 1 мкФ? больше 1,3 мкФ? меньше 0,8 мкФ?