Лабораторная работа М-02

Определение момента инерции тела

по методу крутильных колебаний

Цель работы: Определение момента инерции тела методом крутильных колебаний. Проверка справедливости теоремы Гюйгенса-Штейнера.

Приборы и принадлежности: лабораторная установка, грузы сферической формы, секундомер, штангенциркуль, весы и разновески.

Введение

Поступательное и вращательное движения являются частными проявлениями общего процесса механического движения материи. Физическое единство отражается в аналогии математической формы записи законов, описывающих эти виды движения. Основной закон динамики поступательного движения описывается выражением

или (2.1)

Величина m – масса тела – выражает численно меру инертности тела, т.е. его способность изменять состояние поступательного движения под действием силы . Основной закон динамики вращательного движения твердого тела, вращающегося вокруг оси симметрии тела, записывается в виде:

или (2.1а)

где - момент импульса тела,

- вектор углового перемещения,

- угловое ускорение,

- момент силы.

Коэффициент пропорциональности J носит название момента инерции. Момент инерции является мерой инерции тела во вращательном движении и определяет способность тела изменять состояние вращательного движения под действием момента силы . Размерность момента инерции в системе СИ – [кг·м²]. Исходя из размерности момента инерции, можно дать определение момента инерции материальной точки относительно оси вращения в виде

(2.2)

где r_i – радиус вращения материальной точки, а m_i – ее масса. Масса реального тела представляется в виде суммы масс материальных точек его составляющих. Аналогично этому, момент инерции тела есть совокупность моментов инерции его частей, рассматриваемых как материальные точки

(2.3)

Для тел правильной геометрической формы суммирование (а в пределе – интегрирование) по (2.3) дает следующие результаты для моментов инерции вычисленных относительно оси, проходящей через центр симметрии этих тел:

обруч

диск

шар

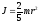
здесь r – радиусы соответствующих тел, а m – их масса. Если необходимо рассчитать момент инерции тела относительно оси АА, не проходящей через центр симметрии, но параллельно ей (рис.2.1), то можно воспользоваться теоремой Гюйгенса-Штейнера: «Момент инерции тела J_AA относительно любой оси АА параллельной оси ОО, проходящей через центр

Рис. 2.1.

симметрии тела, равен моменту инерции J_OO этого тела относительно оси ОО, сложенному с величиной ml²», где расстояние между осями АА и ОО, m – масса тела.

(2.4)

Используя формулы (2.3) и (2.4), можно аналитически рассчитать момент инерции любого тела, условно разделяя его на составные части правильной геометрической формы и определяя расстояния, на которых они находятся от общей оси вращения тела. В случаях, когда аналитическое определение момента инерции затруднено сложностью формы тела или неоднородностью распределения массы, его определяют опытным путем, что и предлагается выполнить в данной лабораторной работе.

Теоретические сведения

Тело, момент инерции которого необходимо определить относительно некоторой оси вращения ОО, проходящей через центр симметрии С тела, жестко скрепляют с этой осью. Если концы оси фиксировать, тело с осью можно рассматривать как крутильный (торсионный) маятник (рис.2.2). Выведенный из состояния равновесия маятник будет совершать колебания с периодом:

(2.5)

Здесь χ (каппа) называется коэффициентом угловой жесткости или модулем кручения подвеса (оси). Численное значение χ выражает величину момента силы, возникающего в материале при его закручивании на единичный угол. Для тела, момент Рис.2.2. инерции J₀₀ которого необходимо определить в опыте,

период колебаний будет иметь величину Т₀₀:

(2.5а)

Если коэффициент угловой жесткости известен, то J₀₀ легко определить из формулы (2.5а). Однако, часто коэффициент угловой жесткости неизвестен. Тогда для определения момента инерции тела J₀₀, чтобы исключить из формулы (2.5а) χ, поступают следующим образом: добавляют к телу, момент инерции которого определяют, дополнительное тело правильной геометрической формы, момент инерции J которого относительно оси 00 маятника легко вычислить по теореме Гюйгенса-Штейнера. Период колебаний такого усложненного маятника станет равным

, (2.6)

Из уравнений (2.5а) и (2.6) выражаем искомый момент инерции J₀₀:

(2.7)

где , m – масса двух шариков,m= m_ш1+m_ш2

Описание экспериментальной установки

Схема экспериментальной установки для проверки теоремы Гюйгенса-Штейнера и определения момента инерции твердого тела изображена на рис.2.3. Тело 1, момент инерции которого J₀₀ необходимо определить, имеет форму цилиндра с кольцом и двумя симметрично расположенными стержнями. Дополнительные грузы 2 – малые шары, надеваются на стержни и могут быть установлены на различных расстояниях l от оси симметрии установки. Ось ОО прикреплена к телу 1 с двух сторон и закреплена в кронштейнах 3. Для приведения системы в колебательно-вращательное движение, необходимо приложить момент силы – повернуть двумя руками стержни на угол 8⁰ – 10⁰. (При малых колебаниях период колебаний не зависит от амплитуды колебаний).

Рис. 2.3

Порядок выполнения работы

1. Определите период колебания тела Т₀ без дополнительных грузов.

2. Установите дополнительные грузы на концах стержней так, чтобы их край совпадал с краем стержня. В таком положении центры масс шаров будут находиться на расстоянии 0,2 м от оси вращения ОО. Измерьте период колебаний Т₁.

3. Измерьте периоды Т₂, Т₃,….Т₆, последовательно передвигая на 2 см шары к центру. Заполните таблицу 2.1.

4. Измерьте диаметр шаров-грузов, найдите величину их радиуса. Определите общую массу двух шаров.

5. Постройте график зависимости , убедившись в справедливости теоремы Гюйгенса-Штейнера. Определите из графика χ- модуль кручения подвеса (оси ОО) и момент инерции J₀₀ маятника относительно оси ОО (см. 2.4, 2.5).

6. Вычислите момент инерции J₀₀ по формуле (2.7). Сравните полученные значения J₀₀.

7. Сделайте вывод о справедливости теоремы Гюйгенса-Штейнера и о совпадении момента инерции J₀₀ маятника, рассчитанного по формуле и определенного из графика. В каком случае точность определения J₀₀ больше и почему?

Таблица 2.1

l1, м

l2, м

l3, м

l4, м

l5, м

l6, м

Т0, с

ΔТ,с

Т1, с

ΔТ,с

Т2, с

ΔТ,с

Т3, с

ΔТ,с

Т4, с

ΔТ,с

Т5, с

ΔТ,с

Т6, с

ΔТ,с

1

2

3

Контрольные вопросы

1. Каков физический смысл момента инерции?

2. Что определяет теорема Гюйгенса-Штейнера?

3. Почему, если график зависимости Т² от l² представляется отрезком прямой линии, это означает, что теорема Гюйгенса-Штейнера справедлива?

4. При длительном пребывании в невесомости космонавты обычно худеют. Как можно измерить массы тела космонавтов в невесомости?