Лабораторная работа м – 05. Определение модуля Юнга при растяжении образца

на приборе Лермантова.

Цель работы: изучение упругой деформации тела и определение модуля Юнга для стальной проволоки.

Приборы и принадлежности: прибор Лермантова, набор грузов, микрометр, лента измерительная, электронные весы, набор стандартных грузов.

Введение

В области упругих деформаций напряжение, возникающее в деформированном теле, пропорционально относительной деформации. В случае продольной деформации образца цилиндрической формы это соотношение (закон Гука) записывается в следующей форме

(5.1)

Где σ-механическое напряжение, F-деформирующая сила, S-площадь поперечного сечения образца, Е-модуль Юнга материала образца; -относительная деформация (l-длина образца).

Если измерить деформирующую силу и соответствущее ей удлинение образца l, то модуль Юнга можно вычислить по формуле:

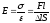(5.2)

Теоретические сведения

Возьмем, однородный стержень и приложим к его основаниям А и В растягивающие или сжимающие силы F (рис. 5.1 а, б). Стержень будет деформирован, то есть, растянут или сжат. Мысленно проведем произвольное сечение С, перпендикулярное к оси стержня. Для равновесия стержня АС необходимо, чтобы на его нижнее основание С действовала сила F₁=F. Это есть сила, с которой нижняя часть стержня ВС тянет верхнюю или давит на нее. Такая сила возникает потому, что нижняя часть стержня деформирована и действует на верхнюю с силой, равной F₁ и противоположно направленную ей.

Такие силы действуют в любом поперечном сечении растянутого или сжатого стержня. Таким образом, деформация стержня связана с возникновением упругих сил, с которыми каждая часть стержня действует на другую, граничащую с ней . Силу, отнесенную к единице площади поперечного сечения стержня, называют механическим напряжением. В рассматриваемом случае напряжение перпендикулярно поперечному сечению стержня. Если стержень растянуть, то это напряжение будет называться натяжением и определяется выражением

, (5.3)

где S – площадь поперечного сечения стержня.

Если стержень сжат, то напряжение называется давлением и численно определяется по формуле

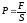. (5.4)

Давление можно рассматривать как отрицательное натяжение и наоборот, то есть Р= -Т.

Рис.5.1. Пусть l₀ – длина недеформированного стержня. После приложения силы F его длина получает приращение D l и делается равной . Отношение

(5.5)

называется относительным удлинением стержня. Относительное удлинение, взятое с противоположным знаком, называется относительным сжатием. Опыт показывает, что для не слишком больших упругих деформаций натяжение Т или давление Р пропорционально удлинению (или относительному сжатию). Это утверждение выражает закон Гука для деформаций растяжения или сжатия стержней и записывается как

и (5.6)

Здесь Е – постоянная, зависящая только от материала стержня и его физического состояния. Она называется модулем Юнга и выражается формулой

(5.7)

Из формулы (5.7) видно, что модуль Юнга равен такому натяжению, при котором длина стержня удваивается, то есть

при .