ЭЛЕКТРОТЕХНИКА / Электротехника и электроника Конюшенко 2007

211

Принцип действия асинхронного двигателя основан на взаимодействии токов в короткозамкнутых витках, расположенных во вращающейся части двигателя – роторе – с вращающимся магнитным потоком, создаваемым обмоткой, размещенной в пазах неподвижной части двигателя – статоре. Магнитный поток при своем вращении пересекает обмотку ротора и индуцирует в ней ЭДС. Индуцируемая ЭДС создает ток, направление которого совпадает

снаправлением ЭДС, определяемой по правилу правой руки.

Врезультате взаимодействия проводников обмотки ротора, по которых проходят токи, с вращающимся магнитным полем возникают электромагнитные силы, направления действия которых согласно правилу левой руки совпадает с направлением вращения магнитного потока. Действие электромагнитных сил создает электромагнитный момент.

На рис. 3.2 показана принципиальная схема действия асинхронного двигателя. Магнитный поток Ц , вращающийся с частотой n0 , об/мин (с угло-

вой скоростью 0 , рад/с), пересекает стержни обмотки ротора, индуцируя в

них ЭДС. Крестиками и точками показано направление тока в стержнях обмотки. Возникающий в роторной обмотке ток, взаимодействуя с магнитным полем, создает электромагнитные силы F . В результате образуется вращающий момент и ротор начинает вращаться. В установившемся режиме выполняется неравенство n n0 ( 0 ). Так как ротор вращается асинхронно (не-

синхронно) с магнитным полем, то электродвигатель называется асинхронным.

В простейшем случае в пазах статора размещаются три катушки (обмотки) с пространственным смещением друг относительно друга на 120º. Каждая из катушек создает пульсирующий синусоидальный магнитный поток. Магнитные потоки смещены по фазе друг относительно друга на 120º:

фА Фm sin щt ,

, фB Фm sin(щt 120 )

.фC Фm sin(щt 120 )

Для определения результирующего магнитного потока магнитные потоки ЦA , ЦB , ЦC изображают на плоскости системы прямоугольных декарто-

вых координат, на которой размещены катушки статорной обмотки (рис. 3.3, а). Магнитный поток A пульсирует перпендикулярно плоскости катушки A-

X, B - перпендикулярно плоскости катушки B-Y, C - перпендикулярно

плоскости катушки C-Z. Взяв проекцию всех магнитных потоков на ось x , получают

212

( Ф)x ФA ФB cos 60 ФC cos 60

Фm sin щt Фm sin(щt 120 ) cos 60 Фm sin(щt 120 ) cos 60

32 Фm sin щt .

Проекция магнитных потоков на ось y дает

( Ф)y ФB cos30 ФC cos30 32 Фm cosщt

Составляющие ( Ф)x и ( Ф)y магнитного потока, каждая из которых

пульсирует вдоль своей оси, расположены под углом 90º друг относительно друга. Результирующий магнитный поток

тельно, в зависимости от времени результирующий магнитный поток изменяет свое положение в пространстве.

Находят отношение составляющих ( Ф)x и ( Ф)y :

На рис 3.3, б изображена диаграмма, на которой даны составляющие магнитного потока и результирующий поток Ф. Из диаграммы видно, что tg tg t , а следовательно, угол t и зависит от времени t и угловой час-

тоты . За время одного периода T магнитный поток повернется на угол

213

бФ 2рf1Ф 2рФ1 Ф 2р.

Как видно из данного выражения магнитный поток за один период поворачивается на угол 2 , т.е совершает один оборот. Тогда за одну секунду магнитный поток совершит f оборотов. Частота вращения магнитного по-

поток совершит 24 000 об/мин.

Частота n0 (угловая скорость 0 ,) вращения магнитного поля зависит не только частоты f1 питающего напряжения, но и от числа полюсов самого магнитного поля:

n0 60 f1 /p об/мин,

где p число пар полюсов вращающегося магнитного поля. Угловая

скорость вращения магнитного поля

0 2рn0 / 60 2р60 f1 /( 60 p) 2рf1 /p рад/с.

Многополюсные асинхронные двигатели получают за счет конструкции обмотки статора.

Вращающееся магнитное поле может быть возбуждено и двухфазной системой напряжений при условии, что обмотки статора в пространстве смещены на 90º и напряжения, питающие статорную обмотку, имеют фазовый сдвиг 90º.

3.1.2 Основные уравнения асинхронного двигателя при неподвижном и вращающемся роторе

При анализе режимов работы асинхронного двигателя удобно пользоваться безразмерной величиной, называемой скольжением (S), под которой понимают разность скоростей (частот) вращения магнитного поля статора ( n0 ) и ротора ( n2 ), отнесенная к скорости (частоте) вращения магнитного по-

ля статора, т.е.:

214

S n0 n2 . n0

Или через угловую скорость:

S0 2 .

0

Частота вращения ротора всегда меньше частоты вращения магнитного поля, так кА в случае их равенства магнитное поле не будет пересекать роторную обмотку, и ЭДС ротора, а следовательно, и ток в его обмотке стал бы равен нулю, что привело бы к исчезновению электромагнитных сил, которые создают вращающий момент

Значения скольжения асинхронного двигателя изменяются от S=1 (при пуске, когда n=0), до S= Sном , что соответствует номинальной нагрузке двига-

теля. Номинальное скольжение современных асинхронных двигателей находится в пределах Sном =2…5%. Скольжение холостого хода Sх не превышает

1%.

Как указывалось выше, ЭДС в обмотках статора и ротора создаются в результате относительного вращения магнитного поля и обмоток, при котором линии магнитного поля пересекают участки (стержни) обмоток, находящиеся в пазах статора и ротора. Для определения ЭДС и её направления принято рассматривать движение проводника относительно неподвижного магнитного поля (правило правой руки). Тогда ЭДС в любом из проводников статора или ротора eпр Blv , где B – магнитная индукция в воздушном зазоре

(в месте нахождения проводника); l – длина проводника, пересекаемого магнитным полем (длина магнитопровода машины); v – линейная скорость движения проводника в магнитном поле, которое распределяется синусоидально вдоль воздушного зазора.

Среднее значение ЭДС в одном витке обмотки

Eср вит 2Bсрlv ,

где:

215

Bср Фп/Sп Фп/(lф) ;

Фп 32 Фm ,

ф рD/( 2 p) ,

D – внутренний диаметр статора.

Значение ЭДС в одной фазе обмотки статора

E1 сс Eср витw1 2Bсрlv0 w1 ,

где

w1 - число витков одной фазы обмотки статора,

v0 0 D/ 2 ,

0 2рn0 / 60 - угловая скорость вращения магнитного потока. Максимальное значение ЭДС статорной обмотки

E1 m р2 E1 сс .

Произведя следующие замены, получают

E1 m 2рw1 f1Фп .

Для учета влияния размещения обмотки в пазах статора на ЭДС витков, приводящего к неравенству геометрической и алгебраической сумм ЭДС

витков обмотки E вит Eвит , вводят обмоточный коэффициент

kоб E вит / Eвит . Тогда:

218

Уравнение (3.8) показывает, что асинхронный двигатель с вращающимся ротором подобен трансформатору, у которого к вторичной обмотке подключена нагрузка:

RH r2 1 S S .

Величина сопротивления RH зависит от скольжения, а скольжение – от нагрузки на валу двигателя. Следовательно, сопротивление RH является эквивалентом нагрузки двигателя.

Величины приведенного ротора обозначают теми же символами, что и неприведенного, но со штрихом. Определим соотношения между величинами в приведенном и реальном роторах.

Для напряжений и ЭДС ротора:

где KU w1 kоб1 . w2 kоб2

Коэффициент KU называют коэффициентом приведения по напряже-

нию.

Для токов и магнитодвижущих сил ротора:

219

Коэффициент KI называют коэффициентом приведения по току.

С учетом равенства потерь в реальном и приведенном роторах имеем:

m1 (I '2 )2 R'2 m2 I22 R2 .

Следовательно:

R'2 R2 m1 W1 kоб1 2 ; m2 W2 kоб2

или R'2 KГ R2 ,

где: KГ m1 W1 kоб1 2 , m2 W2 kоб2

Коэффициент KГ называют коэффициентом приведения по сопротив-

лению.

С учетом полученных коэффициентов приведения ( KU , KI , KГ ) уравне-

ния электрического и магнитного состояния асинхронного двигателя с вращающимся ротором будут иметь следующий вид:

Уравнениям (3.8-3.10) соответствует схема замещения, показанная на рис.3.4.

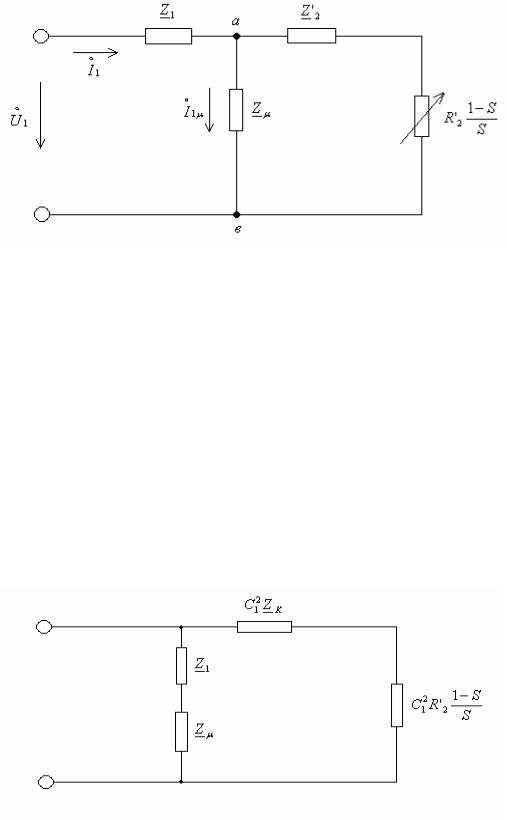
220

Рис.3.4

Сопротивление Z называют сопротивлением намагничивания. Как и в

трансформаторе оно зависит от напряжения U1. С повышением этого напряжения сопротивление Z уменьшается.

Изображение на рис.3.4 схема называется Т-образной схемой замещения. Эта схема полностью отражает физические процессы, происходящие в асинхронном двигателе, но имеет узловую точку (а) между сопротивлениями Z1 и Z'2 , что усложняет расчет токов при различных значениях скольжения.

Поэтому большое практическое применение для анализа режимов работы асинхронного двигателя находит другая схема замещения, в которой намагничивающая ветвь подключена непосредственно на вход схемы, куда подводится напряжение U1 . Эта схема показана на рис.3.5, её обычно называют Г-

образной схемой замещения асинхронного двигателя:

Рис.3.5

На рис.3.5 приняты следующие обозначения: