ЭЛЕКТРОТЕХНИКА / Электротехника и электроника Конюшенко 2007

151

Для примера определим напряженность прямого проводника с током в некоторой точке А магнитной силовой линии (рис. 1.81).

Магнитные силовые линии прямого проводника с током имеют вид концентрических окружностей и вследствие симметрии напряженность поля во всех точках, равноудаленных от оси проводника, одинакова. Направление вектора напряженности определяем по правилу правоходового винта. В качестве контура выберем окружность радиуса а, совпадающую с

силовой линией поля.

Так как контур совпадает с магнитной силовой линией, величина вектора напряженности и его проекция на касательную в любой точке равны между собой. Поэтому в формуле закона полного тока подынтегральное выражение будет скалярным произведением, причем Н можно вынести за знак интеграла.

Н d I

H 2 a I.

Таким образом, напряженность магнитного поля

Определим напряженность магнитного поля и магнитный поток внутри кольцевой катушки индуктивности (тороида) с равномерно распределенной обмоткой, обтекаемой током I (рис. 1.82).

Пусть обмотка имеет w витков, площадь поперечного сечения витка S, абсолютная магнитная проницаемость материала тороида

152

Если разница радиусов внешней и внутренней окружностей тороида невелика, то длины магнитных силовых линий мало отличаются от длины lср средней линии.

Контур магнитной силовой линии охватывает один и тот же ток столько раз, сколько витков w имеет тороид. Поэтому закон полного тока в этом случае имеет вид

Hdl wI,

Так как напряженность поля Н вдоль силовой линии одинакова, то ее можно вынести за знак интеграла

H dl wI,

откуда

Произведение wI равно МДС F обмотки. Таким образом, напряженность магнитного поля внутри тороида равна магнитодвижущей силе, приходящейся на единицу длины тороида.

Определим поток Ф магнитной цепи, замыкающийся внутри тороида. При достаточно равномерном распределении магнитной индукции по сечению

Выражение в знаменателе можно трактовать как магнитное сопротивление Rм. Следовательно, магнитный поток Ф в веберах равен частному от деления МДС F в амперах на магнитное сопротивление Rм. в генри в минус

153

первой степени (Гн-1):

Полученное выражение закона магнитной цепи подобно выражению закона Ома для электрической цепи.

Вычислим напряженность магнитного поля цилиндрической катушки конечной длины (рис. 1.76). При l d можно рассматривать такую катушку как часть тороида с бесконечно большим радиусом. Тогда на основании (1.64) магнитодвижущая сила, приходящаяся на единицу длины катушки l, даст значение напряженности поля внутри катушки:

На практике принято, что для определения напряженности магнитного поля в точках внутри катушки при l 5d можно пользоваться формулой

(1.66).

Пример 1.5.2. Некоторые современные автомобильные катушки зажигания изготовляют с замкнутым магнитопроводом по схеме рис. 1.83.

Рис. 1.83

Определить индуктивность первичной обмотки, имеющей w 80 витков

медной проволоки, по которой проходит постоянный ток I = 4 А. Магнитопровод набран из листов электротехнической стали 2013 и имеет в сечении форму квадрата со стороной b = 21 мм. Суммарная толщина прослоек изоляции между листами = 1мм. Длина каждого стержня а = 80 мм.

154

Примечание. Схема катушки зажигания является условной, так как первичную обмотку и вторичную с числом витков w2 наматывают на один

стержень, причем первичную поверх вторичной.

Решение. 1. Определяем длину средней магнитной линии lср:

lср = 4а - 4b = 4 80 - 4 21 = 236 мм = 0,236 м.

2. Магнитное поле катушки зажигания можно считать сосредоточенным внутри сердечника, так как магнитный поток рассеяния, замыкающийся по воздуху, обычно незначительный.

Напряженность магнитного поля не зависит от наличия магнитопровода и примерно одинаковая по всей длине средней магнитной линии. Поэтому для ее вычисления можно воспользоваться формулой для тороида (1.64):

H w1 I 80 4 1356 А/м. lcp 0.236

3.Зависимость В от Н для стали является нелинейной, и абсолютная магнитная проницаемость стали переменная. Поэтому магнитную индук-

цию нельзя определять по формуле В = аН. Для определения магнитной индукции нужно воспользоваться характеристикой намагничивания стали, заданной в виде кривой 1 на рис. 1.78. Напряженности магнитного поля 1356А/м соответствует магнитная индукция 1,57 Тл.

4.Магнитный поток в любом сечении магнитопровода одинаков:

Ф = В S = В b (b- ) = 1,57 0,21 (0,21-0,01) = 0,0660 Вб.

5. Индуктивность катушки определяется отношением магнитного потокосцепления к току:

155

Вычисленная индуктивность катушки зажигания имеет значение 1,32Гн только при токе I = 4 А. При другом токе индуктивность будет иметь иное значение.

Катушки зажигания с замкнутой магнитной цепью запасают большую электромагнитную энергию, чем традиционные катушки с разомкнутой магнитной цепью.

1.5.4. Расчет неразветвленных магнитных цепей с неоднородным магнитопроводом

Расчет магнитных цепей имеет одну из двух целей: либо определение МДС, необходимой для создания заданного магнитного потока в рабочем зазоре, либо определение значения магнитного потока в рабочем зазоре по заданной МДС. Поэтому при заданных параметрах магнитной цепи различают две постановки задачи.

Прямая задача по заданному магнитному потоку Ф магнитной цепи требуется определить МДС F, обеспечивающую этот поток. Обратная задачапо заданным одной или нескольким МДС требуется определить магнитные потоки, возникающие под их воздействием.

При расчетах магнитных цепей с постоянными МДС обычно принимается, что магнитный поток сосредоточен в стальном магнитопроводе и распределяется равномерно по его сечению, причем в любом сечении поток один и тот же. Принимается также, что в воздушном зазоре магнитный поток ограничен сечением, равным площади поперечного сечения примыкающего участка стального магнитопровода; средняя длина магнитной линии находится простейшими геометрическими построениями. При нахождении связи между напряженностью магнитного поля и индукцией используют только кривую первоначального намагничивания, не принимая во внимание петлю гистерезиса.

Рассмотрим расчет неразветвленной неоднородной магнитной цепи, изображенной на рис. 1.84.

Геометрические размеры и материал магнитопровода известны. Требуется определить МДС, необходимую для создания в зазоре магнитного потока Ф.

Здесь магнитная цепь неоднородна по материалу (содержит воздушный зазор) и по сечению.

Однако в пределах каждого из участков l0, l1, l2, l3, l4 магнитная цепь однородна, т.е. выполнена из одного и того же материала и имеет одно и то же сечение.

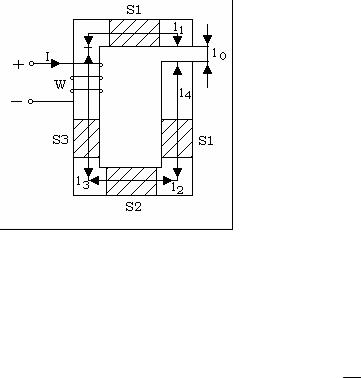
156

Следовательно, напряженность и индукция магнитного поля в пределах каждого участка величины постоянные. Магнитная индукция на отдельных участках стального магнитопровода:

Рис. 1.84

По кривой намагничивания для материала магнитопровода определяем напряженность магнитного поля Н1 = Н4, Н2 и Н3. Напряженность магнитного поля в воздушном зазоре находим по формуле

H0 B0 .

0

По закону полного тока

Hdl wI,

причем интегрирование производится по контуру средней магнитной силовой линии. Интеграл по замкнутому контуру можно заменить суммой интегралов по отдельным участкам:

H1dl H2 dl H3dl H4 dl H0dl wI

Так как в пределах каждого участка напряженность является величиной постоянной, то ее можно вынести за знак интеграла:

Н1l1+Н2l2+Н3l3+Н4l4+Н0l0 = Нklk = wI = F.

157

Эта формула по существу является другой формой записи закона полного тока (1.63).

Таким образом, расчет магнитной цепи при постановке прямой задачи сводится к следующему алгоритму:

1)разбивают магнитную цепь на однородные участки и определяют

геометрические размеры этих участков: площади поперечного сечения Sk и длины lk (по средней длине магнитной силовой линии);

2)определяют магнитную индукцию Вk на каждом из однородных участков по заданному магнитному потоку Ф и рассчитанному сечению Sk;

3)рассчитывают напряженность магнитного поля Нk на каждом из однородных участков стального магнитопровода по кривым намагничивания

ферромагнитных материалов, а напряженность Н0 магнитного поля в воздушном зазоре определяют по формуле

4) искомую МДС находят по закону полного тока:

Следует иметь в виду, что число витков обмотки возбуждения w выбирают с учетом величины питающего ее напряжения, поскольку необходимая МДС может быть создана при любом сочетании величины тока в обмотке возбуждения и числа ее витков.

При решении обратной задачи, когда в магнитной цепи заданы геометрические размеры, кривые намагничивания ее материалов и МДС F, а требуется определить магнитный поток Ф, формулой (1.65) можно воспользоваться только для однородных магнитопроводов.

Для неоднородной цепи не зная магнитного потока Ф, а следовательно, и индукции В, нельзя в (5.6) указать напряженность магнитного поля в ферромагнитном материале и Н0 в воздушном зазоре. Поэтому обратную задачу чаще всего решают графоаналитическим методом. Задаются рядом значений магнитного потока Ф1, Ф2, ... Фn. Для каждого из потоков решают прямую задачу и определяют соответствующие им МДС (wI)1, (wI)2, ... (wI)n. Затем строят вебер-амперную характеристику магнитной цепи Ф = f(wI) (рис. 1.85), по которой определяют искомый магнитный поток Фn по заданной величине МДС (wI)д.

158

Чтобы уменьшить объем вычислительной работы, следует учесть, что максимальный магнитный поток, которым приходится задаваться при расчете, определяют по формуле

Тем самым в первом приближении предполагается, что магнитное сопротивление магнитопровода из ферромагнитного материала равно нулю, а заданная МДС возбуждает магнитный поток только в воздушном зазоре. Формула (1.68) пригодна для предварительных

Рис. 1.85 расчетов при постановке прямой и обратной задач ввиду того, что основное магнитное сопротивление неразветвленной цепи с неоднородным

магнитопроводом определяется воздушным зазором. Например, при относительной магнитной проницаемости ферромагнитного материала=1000 магнитное сопротивление стального сердечника общей длиной 1 м (для цепи, представленной на рис. 1.84, где поперечные сечения на любом участке не сильно отличаются между собой) эквивалентно сопротивлению воздушного зазора толщиной l0 = 1 мм.

Пример 1.5.3. Для электромеханического реле автомобильного регулятора напряжения РР127 известно, что якорек Я будет удерживаться основной обмоткой ОО притянутым к цилиндрическому сердечнику ЦС, преодолевая натяжение пружины П, при магнитной индукции в воздушном зазоре равной В0 = 1 Тл. Минимальное значение воздушного зазора l0 = 1 мм ограничивается алюминиевой вставкой Al, препятствующей прилипанию якорька к цилиндрическому сердечнику (рис. 1.86).

Определить величину МДС, которая обеспечивает указанное значение магнитной индукции. Поперечное сечение S магнитопровода из электротехнической стали 2013 на любом участке равно 2 см2. Длина отдельных участков магнитопровода указана на рисунке в миллиметрах.

Решение. 1. Так как магнитная цепь реле является неразветвленной, то на всех участках магнитный поток Ф одинаков. Величина его не задана, но легко определяемая:

159

Ф = В0S = 1 2 10-4 = 2 10-4 Вб.

По постановке задача является прямой: по известному магнитному потоку требуется определить МДС F, возбуждающей этот поток а, следовательно, и заданную индукцию.

2. Разбиваем магнитную цепь на однородные участки и определяем длину средней линии в сердечнике.

По условию задачи дано, что сечение стального магнитопровода в любом месте одинаково (S = 2 см2). Длина пути магнитного потока по стальному сердечнику

Рис. 1.86

l1 = 40+35+40+35 = 150 мм=0,15м.

3. Напряженность магнитного поля для участков со сталью определяем по кривой намагничивания (рис. 1.78, кривая 1).

Н1 = 110 А/м.

Напряженность магнитного поля в воздушном зазоре

4. Искомую МДС определяем по закону полного тока (1.67):

Н1l1+Н0l0 = F.

110 0,15+0,8 106 0,001 = 16,5+800 = 816 А.

160

Такая МДС может быть получена при помощи катушки с 816 витками при токе I = 1 А или же при помощи катушки с 408 витками и токе I = 2 А. В данном случае при выборе соотношения между числом витков и значением тока решающими факторами являются рабочее напряжение на зажимах катушки, сопротивление провода обмотки, а также возможность размещения ее на цилиндрическом стержне с учетом расстояния до бокового стержня.

1.5.5 Расчет разветвленных магнитных цепей

Магнитные цепи автотракторных генераторов, стартерных электродвигателей, исполнительных механизмов с электромагнитным приводом автомобильных систем управления выполняются как симметричные разветвленные. Для примера на рис. 1.87 представлена магнитная цепь аварийного вибратора РС 331, используемого в системах зажигания автомобилей «ГАЗ

6611», «ЗИЛ 130 Е» и др.

Рис. 1.87

Магнитный поток Ф распределяется между двумя ветвями, и в каждой ветви магнитный поток равен Ф/2. Обе ветви представляют собой два параллельно включенных магнитопровода с потоками Ф1 = Ф2 = Ф/2, в которых действует МДС F = wI.

Расчет симметричной разветвленной цепи сводится к расчету одного контура в том порядке, в котором рассчитывают неразветвленные цепи. Для этого условно разделяют разветвленную магнитную цепь на контуры так, чтобы на участках одного и того же контура магнитный поток был один и тот же.

Пример 1.5.4. Катушка аварийного вибратора РС 331 имеет 120 витков.