ЭЛЕКТРОТЕХНИКА / Электротехника и электроника Конюшенко 2007

102

чинают строить с изображения звезды фазных напряжений Ua ,Uв,Uc (рис.

1.54).

Каждый из фазных токов откладывают из начала лучей звезды с учетом угла сдвига фаз (рис. 1.54) между соответствующими векторами тока и напряжения. Сложив геометрические фазные токи (например, путем переноса векторов параллельно самим себе) получают вектор тока в нулевом проводе, и после измерения количества масштабных делений, укладывающихся на его длине, опеделяют численное значение IN.

Так как нагрузки по характеру чаще всего резистивные и резистивноиндуктивные, то при большом числе потребителей в трехфазной сети ток в нулевом проводе обычно намного меньше линейных токов. Поэтому в четырехпроводной системе нулевой провод выполняют с меньшим, чем линейные провода, поперечным сечением.

Для практической работы еще важно знать, что прокладка всех четырех проводов в одной общей металлической трубе или в кабеле с металлической оболочкой не приводит к нагреву трубы или оболочки, так как в любой момент времени геометрическая сумма четырех токов равна нулю, как это следует из формулы (1.37), и такие токи совместно не создают магнитного поля.

Правилами устройства электроустановок (ПУЭ) запрещается использование для четырехпроводных сетей трехжильныхсиловых кабелей в металлической оболочке с отдельной прокладкой нулевого провода.

Рассчет четырехпроводной несимметричной цепи оказался простым, потому что изначально предпологалось существование нулевого провода с очень малым сопротивлением. Он обеспечивает симметрию фазных напряжений при несимметричной нагрузке и соблюдения соответствия между фаз-

ным и линейным напряжением UЛ = 3Uф . Обрыв нулевого провода при не-

симметричной нагрузке приводит к перераспределению или, как говорят, перекосу фазных напряжений. Между общей точкой источника питания появляется напряжение нейтрали UnN , отличное от нуля.

К фазе с большим сопротивлением будет приложено повышенное напряжение, а к фазе с меньшим сопротивлением – пониженное. Повышение напряжения опасно для изоляции приемника и может вызвать перегрев или перегорание приемников. Понижение напряжения на фазах приводит к тому, что они не получают расчетной мощности.

Для предотвращения такого режима следует обращать особое внимание на целостность нулевого провода, не допускать установки в нем плавких предохранителей, выключателей.

103

Обрыв одного линейного провода при неповрежденном нулевом проводе практически не складывается на однофазных приемниках, включенных между неповрежденными линейными проводами и нулевым.

Соединение звезды с нулевым проводом повсеместно используется для электропитания осветительных нагрузок жилых и общественных зданий, производственных однофазных приемников и в других случаях с многочисленными приемниками, выключаемыми и включаемыми независимо друг от друга.

Пример 1.3.1. Электропитание трех смежных комнат студенческого общежития производится по схеме звезда с нулевым проводом. В некоторый момент вечернего времени сложилась ситуация, которая может быть отображена схемой на рис. 1.55. К фазе А подключена комната № 1, где для освещения используют 4 одновременно горящие лампы номинальной мощностью по 100 Вт каждая. К фазе В подключена соседняя комната № 2, где в это время горит только одна такая же лампа. Из комнаты № 3, подключенной к фазе С, студенты ушли в библиотеку изучать электро-технику и все электрические приборы выключили. Номинальное напряжение потребителей UН = 220 В, линейное напряжение сети UЛ = 380 B. Определить токи в фазах при нормальном режиме и дать анализ аварийного режима, возникшего в результате случайного обрыва нулевого провода.

Рис. 1.55

Решение.

1. Определим фазные токи в нормальном режиме. Так как нагрузка активная, то выражения активной мощности будут очень просты:

104

Pa UфIa ,

Pb UфIb, Pc 0.

При наличии нулевого провода каждая включенная лампа находится под фазным напряжением

Uф U3Л 3803 220 В,

которое является для них номинальным.

Pa = 4 100 = 400 Вт, Pb = 100 Вт, Рc = 0.

2. Рассмотрим аварийный режим при обрыве нулевого провода. Предварительно определим сопротивления фаз (будем считать, что они при других напряжениях остаются остоянными).

Последовательно включенные приемники в фазах А и В окажутся под линейным напряжением UАВ = 380 В, как это показано на рис. 1.56.

Ток Ia будет одинаковым для двух

приемников (иметь в виду, что приемник в комнате № 1 содержит 4 лампы)

Рис. 1.56

105

Определим напряжения на лампах фаз A и В:

В комнате №1 четыре параллельно включенные лампы окажутся под напряжением значительно меньше номинального и накал их нитей резко уменьшится. Лампа в комнате № 2 ярко вспыхнет и, вероятно, через несколько минут перегорит, после чего обе комнаты окажутся без освещения.

Рассмотренный пример показывает, насколько важно сохранять неповрежденным нулевой провод.

1.3.3 Расчет соединения приемников звездой при симметричной нагрузке

Наибольшее распространение в народном хозяйстве получили двигатели переменного тока – асинхронные и синхронные. Их статоры состоят из трех фаз с одинаковыми параметрами и подключаются к трехфазной сети. Такие приемники называются трехфазными. Трехфазными выполняются крупные печи и другие электротермические устройства, некоторые электромагниты. Так как фазы таких приемников имеют одинаковые па-метры, то будут справедливы равенства:

и нагрузка называется симметричной.

Первоначально будем считать, что фазы симметричной нагрузки соединены звездой и подключены к четырехпроводной сети по схеме рис. 1.53. Как и в предыдущем параграфе предполагаем, что все четыре провода имеют пренебрежимо малые сопротивления. Следовательно, система фазных напряжений на нагрузке будет симметричной:

Ua Ub Uc Uф U3Л .

106

Ток в любой фазе нагрузки может быть определен по закону Ома:

Iф Uф .

Zф

Вследствие равенства полных сопротивлений фаз и их активных и реактивных составляющих, фазные токи Ib, Ic будут равны по величине и сдви-

нуты от соответствующих фазных напряжений на равные углы, а также будут равны между собой и равны фазным линейные токи:

Ia Ib Ic Iop I A IB IC I Л ,

cos a cos b cos c cos Rф .

Zф

На векторной диаграмме получим симметричную систему токов, где векторы токов сдвинуты по фазе относительно друг друга на угол 1200 (рис. 1.57)

Геометрическая сумма этих токов равна 0:

Ia Ib Ic IN 0 .

Поскольку при симметричной нагрузке в нулевом проводе тока нет, можно его не прокладывать. Тогда четырехпроводная система превращается в трехпроводную. Такие

107

Активная мощность трехфазной системы вследствие равенства активных мощностей фаз будет равна:

(1.39) фазные величины линейными, получаем выражение активной мощности трехфазной цепи:

Соответственно реактивная мощность

а полная мощность

S 3 U Л I Л , или S P2 Q2 . (1.42)

Пример 1.3.2. В качестве источника питания ремонтного цеха автопредприятия используется трехфазный трансформатор ТМ 63/10 номинальной мощностью SH = 63 кВА. Фазы вторичной обмотки трансформатора соединены звездой, и проложенная от него сеть характеризуется линейным напряжением UЛ = 380 В. Для защиты трансформатора во вторичной обмотке применены предохранители в каждом линейном проводе с номинальным током плавкой вставки IПН = 100 А.

В цехе установлено несколько одинаковых трехфазных асинхронных двигателей. Номинальные данные одного двигателя: механическая мощность

108

на валу PH = 7,5 кВт, КПД H = 0,875, cos H = 0,86, фазы статора соединены звездой.

Сколько таких двигателей могут работать в номинальном режиме одновременно, не вызывая перегрузки трансформатора по току?

Решение. 1. Один трехфазный асинхронный двигатель, работая в номинальном режиме, потребляет из сети активную мощность

2. Полная (расчетная) мощность потребления энергии одним двигате-

лем

3. Одновременно могут работать двигатели (целое число):

4. Линейный ток одного двигателя в номинальном режиме на основа-

нии (1.40)

5. Одновременно работающие 6 двигателей потребляют ток

I*Л = 6 IЛ = 6 15,16 = 90,96 A = 91 A,

109

что меньше тока плавкой вставки предохранителя.

Включение еще одного двигателя вызовет перегрузку трансформатора по току, хотя по активной мощности он будет недогружен.

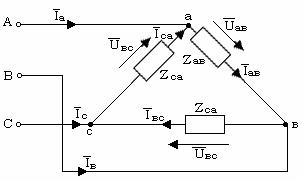
1.3.4 Расчет соединения приемников треугольником при симметричной нагрузке

В тех случаях, когда номинальное напряжение на фазу трехфазного симметричного приемника равно линейному напряжению сети, их включают треугольником рис. 1.58. Фаза приемника включена непосредственно между линейными проводами, поэтому для данной схемы справедливо соотношение

UЛ = Uф.

Условные положительные направления фазных и линейных токов, а также напряжений показаны на схеме.

Рис. 1.58

Если не учитывать падения напряжения в обмотках источника и в линейных проводах, фазные напряжения на нагрузке, равны Uab , Ubc , Uca , будут

равные линейным напряжениям сети UAB,UBC,UCA, образуя симметричную систему напряжений рис. 1.59. При симметричной нагрузке фазные токи, как и напряжения, будут одинаковы по величине и сдвинуты между собой на угол 1200:

110

cos Rф ,

Zф

где для сопротивлений приняты обозначения предыдущего параграфа и учтено, что Zab Zbc Zca Zф. На основании первого закона Кирхгофа для уз-

лов a, b, c можно составить следующие уравнения:

IC Ica Iba ,

т.е. линейный ток равен геометрической разности двух

соответствующих фазных токов.

Рис. 1.59

Этой группе уравнений удовлетворяет векторная диаграмма на рис.

1.59.

Из любого треугольника фазных и линейных тоов находим:

Активная мощность трехфазной симметричной нагрузки при соединении фаз треугольником

Р = 3Рф = UфIф cos ,

или через линейные токи и напряжения