
- •1. КИНЕМАТИКА ТОЧКИ
- •1.1. Краткие теоретические сведения
- •1.2. Задание К1. Исследование движения точки при координатном способе задания движения
- •1.3. Пример 1 выполнения задания К1
- •1.4. Пример 2 выполнения задания К1
- •2. ПЛОСКОПАРАЛЛЕЛЬНОЕ (ПЛОСКОЕ) ДВИЖЕНИЕ ТЕЛА
- •2.1. Краткие теоретические сведения
- •2.2. Задание К2. Исследование движения плоского механизма
- •2.3. Пример выполнения задания К2
- •3. СЛОЖНОЕ (СОСТАВНОЕ) ДВИЖЕНИЕ ТОЧКИ
- •3.1. Краткие теоретические сведения
- •3.3. Пример выполнения задания К3
- •4. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- •4.1. Краткие теоретические сведения
- •4.2. Задание С1. Определение реакций опор твердого тела под действием плоской системы сил
- •4.3. Пример выполнения задания С1
- •4.5. Пример выполнения задания С2
- •5. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- •5.1. Краткие теоретические сведения
- •5.3. Пример выполнения задания Д1
- •6.1. Краткие теоретические сведения
- •6.2. Задание Д2. Применение теоремы об изменении кинетической энергии к исследованию движения механической системы
- •6.3. Пример выполнения задания Д2
- •7. ОСНОВНЫЕ ПОНЯТИЯ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
- •7.1. Краткие теоретические сведения
- •7.3. Пример выполнения задания Д3
42
ЧА С Т Ь II. С Т А Т И К А
4.СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Краткие теоретические сведения
Статикой называется раздел механики, в котором изучаются условия равновесия материальных тел, находящихся под действием сил.
Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с неподвижным телом.
В статике в качестве модели реального материального тела рассматри-
вается абсолютно твердое тело, расстояние между любыми двумя точками которого не изменяется.
Мерой взаимодействия материальных тел в механике является сила.
Сила FG − векторная величина, действие которой на тело определяется модулем, направлением и точкой приложения. Прямая, вдоль которой
направлен вектор F, является линией действия силы.
Совокупность сил, действующих на тело, называется системой сил. Если линии действия сил лежат в одной плоскости, то система сил является плоской, если в пространстве − пространственной. Система сил, у которых линии действия пересекаются в одной точке, называется сходящейся.
Две системы сил, оказывающие на тело одинаковое действие, являются эквивалентными. Система сил, под действием которой свободное твердое тело находится в покое, называется уравновешенной или эквивалентной нулю.
Тело, перемещениям которого в пространстве препятствуют какиенибудь другие, скрепленные или соприкасающиеся с ним тела, является несвободным. Всё, что ограничивает перемещение данного тела в пространстве, называется связью.
Сила, с которой связь действует на тело, препятствуя тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу.
Одним из основных положений теоретической механики является
принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями связей. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного, находящегося под действием активных (заданных) сил и реакций связей.

43
Связи и направления их реакций. Рассмотрим наиболее часто встречающиеся связи и направления их реакций.
Г л а д к а я п л о с к о с т ь (п о в е р х н о с т ь) и л и о п о р а.
Реакция N гладкой плоскости (поверхности) (рис. 4.1, а) или опоры (рис. 4.1, б) направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке.
Г и б к а я н и т ь (провода, канаты, цепи, ремни). Реакция Т нити направлена от тела вдоль нити к точке подвеса (рис. 4.1, в).
Н е в е с о м ы й с т е р ж е н ь с ш а р н и р а м и. Реакция N шарнира направлена вдоль невесомого стержня. Обычно реакция N изображается от тела по стержню в предположении, что в равновесии стержень растянут
(рис. 4.2, а).
Н е п о д вG и ж н ы й ц и л и н д р и ч е с к и й ш а р н и р (подшипник). Реакция RA цилиндрического шарнира А лежит в плоскости Аху, пер-
пендикулярной оси шарнира, и может иметь любое направление. Обычно RA раскладываютG G в точке А на две взаимно перпендикулярные составляющие ХA и YA вдоль декартовых осей (рис. 4.2, б).
|
|
|
NC |
TA |
|
TB |
N |
|
B |
C |
|
||
A |
|
|
|
A |
|
B |
A |
A |
|
|
|
||
|
|
|
|
|
||
|
NB |
|
|
|
||
|
|
|
|
|
||
|
|
NA |
|
|
|
|
а |
|
|
б |
|
в |
|
|
|
|
Рис. 4.1 |
|
|
|
|
y |
|
|
|
|
|
NA |
YA |
|
RA |
Y |
|
R |
A |
|
|
A |
|
A |
|
|
|
|
|
|
|
|
B |
A |
|
x |
mA |
A |
X |
NB |
|
|
XA |
|
||
|
|
|
|
A |
||
|
|
|
|
|
||
а |
|
|
б |
|
|
в |
|
|
Рис. 4.2 |
|
|
|
|

44
Ж е с т к а я з а д е л к а. Нахождение реакции жесткой заделки сводится к определению составляющих ХA и YA , препятствующих линейному
перемещению точки А балки в плоскости действия активных сил, и алгебраической величины реактивного момента mA, препятствующего вращению балки под действием заданных сил (рис. 4.2, в).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ш а р н и р н о - п о д в и ж н а я о п о р а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(опора на катках). Реакция RGВ проходит через |
|||
|
|
|
|
|
|
|
|
|
R |
|||||||||
R |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
B |
ось шарнира В и направлена перпендику- |
|||
|
|
|
B |
|
|
|
|
|
B |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лярно к опорной поверхности (рис. 4.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С ф е р и ч е с к и й ш а р н и р – это |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.3 |
устройство (рис. 4.4, а), допускающее сфе- |
|||||||||
|
|
|
|
|
|
|
|
рическое движение тела 3 вокруг неподвиж- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной точки А (центр внутренней сферы 1), |
с которой жестко скреплено рассматриваемое тело 3. При условии, что сферическая поверхность 2 идеально гладкая, реакция RA направлена в точке А по нормали к этой поверхности. Обычно на схемах реакцию RGA сферического
GG Gраскладывают на три взаимно перпендикулярные составляющие
ХA , YA , ZA , неизвестные по величине.
По д п я т н и к (рис. 4.4, б) представляет собой соединение цилиндрического шарнира 2 с опорной плоскостью 3, на которую опирается вал 1. Реакция подпятника складывается из реакции цилиндрического подшипника, которая раскладывается в плоскости 3, перпендикулярной его оси, на две
взаимно перпендикулярные составляющие ХA и YA , и нормальной реакции ZGA опорной плоскости 3.
|
z |
3 |
z |
|
1 |
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ZA |
|
2 |
|
|
|
|
|
y |
ZA |
|
N |
R |
||
|
|
|
|
||||
|
A |
YA |
A |
|
YA |
y |
|
x |
XA |
|
XA |
3 |
|
|
F |
|
|
|
|
|
|
|
тр |
|
а |
|
б |
|
|
|
в |
|
|
|
Рис. 4.4 |
|
|
|
|

45
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
б |
|
|
в |
|
|||||||
|
|
|
|
|
|
Рис. 4.5 |
|
|
|
|
|
|
|
||
Ш е р о х о в а т а я |
н е п о д в и ж н а я |
п о в е р х н о с т ь. Реакция |
|||||||||||||
шероховатой поверхности представляет собой равнодействующую RG |
силы |
||||||||||||||
нормальной реакции NG и силы трения Fтр (рис. 4.4, в). |
|
||||||||||||||
Две основные задачи статики. В статике решаются две задачи:
1)задача о приведении системы сил заключается в замене данной сис-
темы сил другой, более простой, ей эквивалентной;
2)задача о равновесии состоит в определении условий, при которых система сил, приложенная к телу, будет уравновешенной системой.
Проекцией силы F на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между вектором силы и положительным направлением оси (рис.4.5):
FX = F cosα, |
(4.1) |
где F − модуль силы F ; α − угол между вектором F и положительным направлением оси X.
Проекция силы положительна, если угол α острый (рис. 4.5, а). Проекция силы отрицательна, если угол α тупой (рис. 4.5, б):
FX = Fcos α = Fcos (180º – β) = – Fcos β.
Проекция силы на ось равна нулю, если α = π (рис. 4.5, в).
G 2
Силу F в декартовой системе координат ОXYZ можно аналитически задавать, зная координаты точки А ее приложения и проекции FX , FY , FZ
силы на декартовы оси. Вектор силы F , ее модуль и косинусы углов между силой и координатными осями определяются по формулам
F = FX i + FY |
Gj + FZ k ; |
(4.2) |
||
F = F |
2 +F |
2 +F 2 |
; |
(4.3) |
X |
Y |
Z |
|
|

|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
G G |
|
F |
|
G G |
|
F |
|
G G |
|
F |
|
|
cos F i |
= |
X ; |
cos F j |
= |
Y ; |
cos F k |
= |
Z |
. |
(4.4) |
|||
|
|||||||||||||
|
|
|
F |
|
|
|
F |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь iG, Gj, kG −орты декартовых осей ОX, ОY, OZ соответственно. Следовательно, согласно (4.2) любую силу F можно разложитьG на три
взаимно перпендикулярные составляющие FX = FX i , FY = FY Gj и FZ = FZ k, модули которых равны модулям проекций силы на соответствующие декар-
товы оси. |
G |
G |
G |
G |
|
||||
Если на тело действует система сходящихся сил |
GF1, F2 |
, F3 |
, ..., Fn , |
|
линии действия которых пересекаются в точке О, то сила R , |
эквивалентная |
|||
этой системе сил, называется равнодействующей: |
|
|
|
|
G G |
G |
G |
G n |
G |
(4.5) |
R = F |
+ F |
+ F |
+... + Fn = ∑ F . |
||
1 |
2 |
3 |
k=1 |
k |
|
Геометрически вектор R определяется построением силового многоугольника (рис. 4.6).
Проецируя (4.5) на декартовы оси, можно найти проекции равнодействующей:
R |
n |
|
|
n |
|
|
n |
|
(4.6) |
= ∑ F |
, R = ∑ F |
, R = ∑ F , |
|||||||
X |
k=1 |
kX |
Y |
k=1 |
kY |
Z |
k=1 |
kZ |
|
где FkX , FkY , FkZ − проекции силы Fk на оси ОX, ОY и OZ соответственно.
Тогда аналитически вектор R , его модуль и направление определяются по следующим формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
R = RX i + RY Gj + RZ k; |
(4.7) |
||||||||||
|
|
|
|
|
|
|
|
|
R = |
R |
2 +R 2 +R |
2 ; |
(4.8) |
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
X |
|
Y |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
G G |
|
|
R |
|
|
||||
|
|
|
|
|
|
|
|
|
cos R i |
= |
|
|
X |
; |
|
|
||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G G |
|
R |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
cos R j = |
|
|
Y |
; |
|
(4.9) |
|||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G G |
|
|
|
R |
|
|
|||
|
|
|
|
|
|
|
|
|
cos R k |
= |
|
|
Z |
. |
|
|
||||
|
|
|
|
|
||||||||||||||||
Рис. 4.6 |
|
|
|
|
|
R |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

47
|
|
|
|
|
|
|
|
|
|
Если абсолютно твердое тело нахо- |
||
|
|
F1 |
|
|
|
|||||||
|
|
|
|
|
|
|
дится в равновесии под действием системы |
|||||
|
|
|
|
|
|
|
|
сходящихся сил F1, FG2 , FG3, ..., |
FGn , то их рав- |
|||
|
O |
F |
2 |
|||||||||
|
|
|
|
|
|
|
|
нодействующая равна нулю: |
|
|
||
F |
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n G |
|
(4.10) |
|
|
|
|
|
|
|
|
|
|
R = ∑ F =0. |
|
|
|
|
|
|
|
|
|
|
|
|
k=1 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 |
|
|
||
|
|
Рис. 4.7 |
|
|
|
|
|
Следовательно, силовой многоугольник, |
||||
|
|
|
|
|
|
|
G |
G |
G |
|||
|
|
|
|
|
|
|
|
|
|
построенный на силах F1, F2 , GF3 |
, ..., Fn , яв- |
|
ляетсязамкнутым, т. е. конец силы Fn совпадает сначаломсилы F1 |
(рис. 4.7). |
|||||||||||
Условие (4.10) называется геометрическим условием равновесия для системы сходящихся сил: необходимым и достаточным условием равновесия твердого тела под действием системы сходящихся сил является замкнутость силового многоугольника, построенного на этих силах.
Аналитически условие (4.10) означает, что
n |
|
n |
|
n |
|
|
∑FkX |
=0, |
∑FkY |
=0, |
∑FkZ |
=0. |
(4.11) |
k=1 |
|
k=1 |
|
k=1 |
|
|
Уравнения (4.11) называются аналитическими условиями равновесия плоской системы сходящихся сил: для равновесия абсолютно твердого тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы суммы проекций этих сил на каждую координатную ось были равны нулю.
При действии на твердое тело, находящееся в равновесии, плоской системы трех непараллельных сил, часто используется теорема о трех силах:
если на абсолютно твердое тело, находящееся в равновесии, действуют три силы, лежащие в одной плоскости, то линии их действия пересекаются в одной точке.
G |
G |
Моментом силы относительно центра О называется вектор |
|
|
G |
||
mO (F), равный векторному произведению радиуса-вектора |
r, проведенного |
||
из центра О в точку А приложения силы, на вектор силы F : |
|
||
G |
|
G |
(4.12) |
mO (F ) = r |
×F. |
||
G |
|
О и |
направлен перпендикулярно |
Вектор mO (F) приложен в точке |
|||
плоскости, проходящей через центр О и силу F, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки
(рис. 4.8).
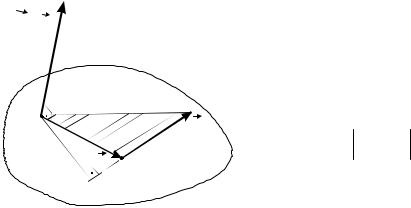
48
m |
( |
O |
F) |
|
G
Момент mO (F) характеризует
вращательный эффект силы F отно-
сительно центра (точки) О. G G
Модуль вектора mO (F) равен
произведениюмодуляF силы наплечо h:
O |
F |
G |
|
|
(4.13) |
||
|
r A |
mO (F) = Fh. |
|
|
h |
Здесь плечо h − перпендикуляр, опу- |
|
|
|
||
|
Рис. 4.8 |
щенный из точки О на линию действия |
|
|
силы F. |
|
|
Свойства момента силы относительно центра:
1.Момент силы относительно центра не изменяется при переносе силы по линии ее действия в любую точку.
2.Если линия действия силы пересекает центр О (h = 0), то момент силы относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки (центра), лежащей в плоскости их действия, пользуются понятием алгебраического момента силы относительно точки. Алгебраический момент
силы F относительно точки О равен взятому с соответствующим знаком произведению модуля силы на ее плечо:
mO (F) = ±Fh. |
(4.14) |
Момент (4.14) считается положительным, если сила стремится повернуть тело в плоскости вокруг точки О против хода часовой стрелки, и отри-
цательным − по ходу часовой стрелки. Например, для сил FG1, FG2 , лежащих
в плоскости ОXY (рис. 4.9), их алгебраические моменты относительно точки В
mB (FG1) = F1h1, mB (FG2 ) = −F2h2.
При вычислении моментов сил удобно пользоваться теоремой Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (точки) О равен сумме моментов сил системы относительно того же центра:
G |
|
G |
n |
G |
|
G |
(4.15) |
m |
O |
(R) = ∑ m |
О |
(F ). |
|||
|
|
k=1 |
|
k |
|
||

49
Y 
F2
A2
O
|
|
|
|
|
F1 |
||
|
h1 |
||
B |
|
|
A1 |
h 2
X
Рис. 4.9 |
Рис. 4.10 |
G |
F относительно центра (точки) О |
|||||
Проекция момента mO (F) силы |
||||||
на ось Z, проходящую через этот центр, называется моментом силы FG |
отно- |
|||||
сительно оси Z, т. е. |
|
|
|
|
||
mZ (F) = |
|
G |
G |
|
cos γ, |
(4.16) |
|
|
|||||
|
mO (F) |
|
||||
G
где γ − угол между вектором mO (F) и осью Z (рис. 4.10).
Из (4.16) имеем, что mZ (F ) − момент силы относительно оси Z является алгебраической величиной, знак которой определяется знаком сos γ:
1)если 0 ≤ γ < 90º, то mZ (F) > 0;
2)если 90º < γ ≤ 180º, то mZ (F) < 0;
3)если γ = 90º, т. е. сила F коллинеарна оси Z, то mZ (FG) = 0.
Величина момента силы относительно оси не зависит от выбора центра (точки) О на оси.
G
В декартовой системе координат вектор mO (F) можно разложить по трем взаимно перпендикулярным направлениям (рис. 4.11):
G G G G G G mO (F) = mX (F)i +mY (F) j +mZ (F)k ,
где mX (FG), mY (FG), mZ (FG) − моменты силы F относительно осей ОX, ОY,
ОZ соответственно.
Существует простое правило вычисления момента силы относи-
тельно оси: для определения момента силы относительно оси следует спроецировать силу на плоскость, перпендикулярную оси, и затем определить алгебраический момент полученной проекции силы относительно точки пересечения данной оси с этой плоскостью (рис. 4.12).

|
|
|
|
|
50 |
|
|
|
|
Z |
mZ( F) |
|
Z |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
m (F) |
|
O k j |
A |
|
Y |
|
|
|
O |
|
|
|||
|
|
|
|
|
i |
|
|
|
|
O |
k |
m (F) |
Y |
h |
|
|
|
|
Y |
|
|
A1 |
|
|
||
) |
i |
j |
|
|
|
FXY |
|
|
(F |
|
X |
|
|
||||
X |
|
|
|
|
|
|||
m |
|
|
|
|
|
|
|
|
|
Рис. 4.11 |
|
|
Рис. 4.12 |
|
|
||
Поэтому |
|
mZ (FG) = mO (FGXY )= ± FGXY h, |
|
|
||||
|
|
|
|
|
(4.17) |
|||
где h – плечо силы FGXY |
– проекции силы F на плоскость ОXY, перпендику- |
|||||||
лярнуюоси Z, относительно точки Опересечения оси Z сэтой плоскостью. |
|
|||||||
В (4.17) |
G |
|
|
|
|
|
||
mZ (F ) будет иметь знак «+», если с конца оси Z сила FXY |
||||||||
видна стремящейся повернуть тело вокруг оси против хода часовой стрелки, |
||||||||
и знак «–» – по ходу часовой стрелки. |
|
|
|
|
||||
Момент силы относительно оси характеризует вращательный эффект силы вокруг оси.
Из (4.17) следуют два важных для практики частных случая:
1)если сила параллельна оси, то ее момент относительно оси равен нулю (FGXY = 0);
2)если линия действия силы пересекает ось, то ее момент относительно данной оси также равен нулю (h = 0).
При вычислении момента силы относительно оси часто пользуются
теоремой Вариньона для моментов силы относительно оси: момент рав-
нодействующей относительно выбранной оси равен алгебраической сумме моментов составляющих сил относительно этой оси.
Проецируя векторное выражение (4.15) на ось Z, получим
|
Z ( |
G |
) |
n |
Z ( |
G |
|
m |
|
k=1 |
k ) |
(4.18) |
|||
|
R |
= ∑ m |
|
F . |
|||

|
|
|
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Парой сил (парой) ( FG, FG′) на- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
зывается система двух равных по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
модулю, параллельных и направлен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ных в |
противоположные |
стороны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сил ( FG |
= −FG′). |
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
лы FG |
Плоскость, в которой лежат си- |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
и FG′, называется плоскостью |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пары, а кратчайшее расстояние d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
между линиями действия сил пары − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
плечом пары (рис. 4.13). |
|
|
|
|
Рис. 4.13 |
|
|
|
||||||||
Пара сил не имеет равнодействующей, так как R = FG + FG′ = 0. Поэтому действие пары сил ( FG, FG′) на абсолютно твердое тело сводится к вращательному эффекту, который характеризуется моментом пары.
Моментом пары называется вектор
G |
(4.19) |
m = F ×d, |
модуль, которого равен произведению модуля одной из сил пары на ее плечо:
m = Fd.
G
Вектор m направлен перпендикулярно плоскости пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки (рис. 4.13). Момент пары есть вектор свободный, т. е. он может быть приложен в любой точке тела.
Для пар, лежащих в одной плоскости, можно не прибегать к векторной символике, а пользоваться понятием алгебраического момента пары. Алгеб-
раический момент пары сил равен взятому с соответствующим знаком
произведению модуля одной из сил пары на плечо пары: |
|
m = ±Fd. |
(4.20) |
Знак « + » в (4.20) соответствует повороту тела в плоскости под действием пары против хода часовой стрелки, знак « » – по ходу часовой стрелки. Например, для пар, лежащих в одной плоскости, изображенной на рис. 4.14, а, алгебраические моменты пар
m1 = F1d1, m2 =−F2d2.

|
F1 |
d1 |
B |
A |
|
F1'
а
52
F |
|
C |
2 |
|
|
|
d |
|
2 |
' |
D |
F2 |
|
Рис. 4.14
m1 m2
б
Следовательно, момент пары равен алгебраическому моменту одной из сил пары относительно точки приложения другой силы пары, т. е.
G m1 = mA(FG1) = mB (F1G′), m2 = mD (F2 ) = mC (F2′).
Поскольку такие пары сил характеризуются только величиной момента, то пары сил, лежащие в одной плоскости, часто изображаются дуговыми стрелками, показывающими направление поворота тела при действии пары
(рис. 4.14, б).
Системой пар называется совокупность нескольких пар, действующих на тело.
G G |
По |
теореме о сложении |
пар, систему пар |
сил |
с моментами |
|||
|
G |
можно заменить одной парой, момент |
G |
которой равен |
||||
m1, m2, ..., mn |
M |
|||||||
геометрической сумме моментов данных пар: |
|
|
|
|||||
|
|
|
G |
G G |
G |
n G |
|
(4.21) |
|
|
|
M = m1+ m2 |
+ ... + mn = ∑mk . |
|
|||
|
|
|
|
|
|
k=1 |
|
|
Задача о приведении произвольной системы сил FG1, FG2 , FG3, ..., FGn
к центру (точке) О, т. е. о замене данной системы сил другой, более простой, ей эквивалентнойG G G ,Gрешается применением теоремы Пуансо: любая система
сил F1, F2 , F3, ..., Fn , действующих на абсолютно твердое тело, при приведении к произвольному центру О заменяется одной силой R , равной главному вектору системы сил, приложенной в точке О, и парой сил с моментом МO , равным главному моменту системы сил относительно центра О:
{G G G G G G
F1, F2, F3, ..., Fn}~ {R, MO}.

53
а |
б |
Рис. 4.15 |
сил F1, FG2 , FG3, ..., FGn на |
Следовательно, действие исходной системы |
твердое тело (рис. 4.15, а) эквивалентно действию на него одной силы R , равной геометрической сумме всех сил системы:
RG= FG1 + FG2 |
+ FG3 +... + |
n |
|
FGn = ∑FGk , |
(4.22) |
||
|
|
k=1 |
|
|
|
|
G |
называемой главным вектором, |
и одной пары с моментом |
МО , равным |
|
сумме моментов всех сил относительно центра О:
G |
G G |
G G |
G G |
n |
G |
G |
(4.23) |
МО =mO(F1) + mO(F2) + ... + mO(Fn) =∑mO(Fk ), |
|||||||
|
|
|
|
k=1 |
|
|
|
называемым главным моментом системы сил F1, FG2 , FG3, ..., FGn относительно этого центра (рис. 4.15, б).
Согласно (4.22) и (4.23) вектор R |
от выбора центра О не зависит, |
|
G |
пары при изменении положения центра О может изменяться |
|
а момент МО |
||
вследствие изменения моментов отдельных сил.
Главный вектор R (4.22) произвольной системы сил в декартовых координатах определяется по модулю и направлению применением полученных выше формул (4.6)–(4.9).
Для вычисления главного момента |
МО (4.23) системы сил |
FG1, FG2 , FG3 , ..., FGn относительно центра (точки) |
О следует начало декартовой |
системы координат ОXYZ поместить в центре приведения О и затем вектор
G
МО разложить по трем взаимно перпендикулярным декартовым осям:
G G |
G |
+MZ k. |
|
MO (F) = MX i +MY j |
(4.24) |
||

54
Здесь МX, МY, MZ − главные моменты системы сил F1, |
FG2 , FG3, |
..., FGn относи- |
|||||||||||||||||
тельно осей ОX, ОY, ОZ соответственно, определяются как проекции главно- |
|||||||||||||||||||
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го момента MO |
на эти координатные оси: |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
n |
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
MX = ∑mX (FGk ), |
MY = ∑mY (FGk ), |
|
MZ = ∑mZ (FGk ). |
|
|
(4.25) |
|||||||||||||
|
k =1 |
|
|
|
|
k=1 |
|
|
|
k=1 |
|
|
|
|
|
|
|||
Модуль и направление главного момента вычисляются по формулам |
|||||||||||||||||||
|
|
|
|
|
MO = M2X +MY2 +M2Z ; |
|
|
|
|
|
|
|
|
(4.26) |
|||||
G |
G |
M |
|
|
G |
G |
M |
|
|
G |
G |
|
M |
Z |
|
|
|||
cos M |
O |
i |
= |
|
X ; |
cos M |
O |
j = |
Y |
; |
cos M |
k = |
|
|
. |
|
|||
M |
|
M |
|
|
|||||||||||||||
|
|
|
O |
|
|
|
M |
|
|
O |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
O |
|
|||
Для равновесия абсолютно твердого тела, находящегося под действием произвольной системы сил, необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т. е.
RG =0 , |
МО =0. |
(4.27) |
Условия (4.27) являются необходимыми и достаточными условиями равновесия тела под действием произвольной системы сил.
Аналитические условия равновесия для различных систем сил
П р о с т р а н с т в е н н а я п р о и з в о л ь н а я с и с т е м а с и л. Если
Z |
|
|
|
абсолютно твердое тело находится |
|
|
|
|
|||
|
|
|
в равновесии под действием произ- |
||
Fn |
|
|
|
||
|
|
|
вольной |
пространственной системы |
|
|
F1 |
|
|
сил (рис. 4.16), то условие (4.27) оз- |
|
O |
|
|
Y |
начает, что при равновесии тела про- |
|
|
|
|
G |
||
F3 |
|
|
екции векторов R и МО на оси де- |
||
|
|
картовой системы координат ОXYZ |
|||
X |
F2 |
|
должны быть равны нулю. С учетом |
||
|
(4.6) и (4.25) получим шесть скаляр- |
||||
|
|
|
|
||
Рис. 4.16 |
|
|
ных уравнений равновесия: |
||

55
n |
|
|
n |
|
1) ∑FkX |
=0; |
4) |
∑mX (FGk ) =0; |
|
k=1 |
|
|
k=1 |
|
n |
|
|
n |
|
2) ∑FkY |
=0; |
5) |
∑mY (FGk ) =0; |
(4.28) |
k=1 |
|
|
k=1 |
|
n |
|
|
n |
|
3) ∑FkZ |
=0; |
6) |
∑mZ (FGk ) =0. |
|
k=1 |
|
|
k=1 |
|
Уравнения (4.28) называются аналитическими условиями равновесия для произвольной пространственной системы сил: для равновесия твер-
дого тела под действием произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.
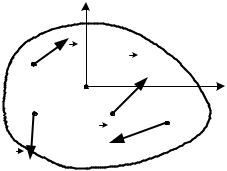
П р о с т р а н с т в е н н а я с и с т е м а п а р а л л е л ь н ы х с и л. Для определенности выберем систему координат так, чтобы ось ОZ была направлена параллельно силам (рис. 4.17). В этом случае уравнения 1, 2 и 6 в (4.28) отсутствуют, так как обращаются в тождества, и аналитические условия равновесия принимают вид
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑FkZ |
=0; |
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑mX (FGk ) =0; |
|
|
|
(4.29) |
|||
|
|
|
|
|
|
k =1 |
(FGk ) =0. |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
∑mY |
|
|
|
|
|
||
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
Fn |
|
Z |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F |
|
|
Fn |
|
|
F1 |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
|
|
O |
|
1 |
Y |
O |
|
|
Y |
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
F2 |
|||
|
|
F3 |
|
|
|
|
F3 |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
X |
|
|
|
|
|
F2 |
|
|
X |
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 4.17 |
Рис. 4.18 |
56
Для равновесия твердого тела под действием пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.
П р о с т р а н с т в е н н а я с и с т е м а с х о д я щ и х с я с и л. В этом случае за центрG приведенияG G Gвыберем точку О, в которой пересекаются
линии действия сил F1, F2 , F3, ..., Fn (рис. 4.18).
Тогда уравнения 4, 5 и 6 системы (4.28) отсутствуют, и аналитические условия равновесия для пространственной системы сходящихся сил имеют вид системы (4.11):
n |
|
n |
|
n |
|
∑FkX |
=0; |
∑FkY |
=0; |
∑FkZ |
=0. |
k=1 |
|
k=1 |
|
k=1 |
|
Для равновесия твердого тела под действием пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей были равны нулю.
П л о с к а я с и с т е м а с х о д я щ и х с я с и л. Если сходящаяся система сил находится в плоскости ОXY, то третье уравнение системы (4.11) обращается в тождество и аналитические условия равновесия принимают вид
n |
|
n |
|
|
∑FkX |
=0; |
∑FkY |
=0. |
(4.30) |
k =1 |
|
k =1 |
|
|
Для равновесия твердого тела под действием плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю.
П л о с к а я п р о и з в о л ь н а я с и с т е м а с и л. Пусть твердое тело находится в равновесииG G G подG действием
системы сил F1, F2 , F3, ..., Fn , лежащих
в одной плоскости, совмещенной с плоскостью ОXY (рис. 4.19). В этом случае уравнения 3, 4 и 5 в (4.28) отсутствуют, а уравнение 6 с учетом (4.17) можно заменить уравнением алгебраических моментов сил относительно точки О. Тогда аналитические условия равновесия можно записать в виде трех уравнений:
n |
|
n |
|
∑FkX |
=0; |
∑FkY |
=0; |
k =1 |
|
k =1 |
|
|
Y |
|
|
B |
Fn |
F2 |
X |
|
O |
||
|
|
|
|
C |
|
D |
A |
|
|
F1 |
|
F3 |
|
|
|
|
|
|
|
|
|
Рис. 4.19 |
|
n |
|
|
|
∑mO (FGk ) =0. |
(4.31) |
||
k =1 |
|
|
|

57
Для равновесия твердого тела под действием произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций сил на каждую из двух координатных осей и сумма моментов относительно любой точки, лежащей на плоскости действия сил, были равны нулю.
Уравнения (4.31) называются первой (основной) формой аналитических условий равновесия для плоской произвольной системы сил.
Отметим, что в математическом отношении система уравнений равновесия (4.31) будет проще, если в ней в качестве точки О, относительно которой составляется третье уравнение моментов, выбрать точку пересечения линий действия двух искомых сил.
Вторая форма уравнений равновесия, эквивалентная системе (4.31), имеет вид
n |
|
n |
n |
∑FkX |
=0; |
∑mA(FGk ) =0; |
∑mB (FGk ) =0. |
k =1 |
|
k =1 |
k=1 |
При этом ось ОX неперпендикулярна прямой АВ, проходящей через точки плоскости ОXY, относительно которых составляются уравнения моментов.
Третья форма уравнений равновесия для плоской произвольной системы сил не содержит уравнений проекций сил на оси:
n |
n |
∑mA(FGk ) =0; |
∑mB(FGk ) =0; |
k=1 |
k=1 |
n G
∑mC (Fk ) =0.
k=1
При этом предполагается, что точки А, В и С плоскости ОXY, относительно которых составляются уравнения моментов, не лежат на одной прямой.
П л о с к а я с и сGт еGм аG п а рGа л л е л ь н ы х с и л. В случае системы параллельных сил F1, F2 , F3, ..., Fn , лежащих в плоскости ОXY, выберем
ось ОX, параллельную силам (рис. 4.20). Тогда в системе (4.31) останется два уравнения равновесия:
n |
|
n |
|
∑FkX |
=0; |
∑mO(FGk ) =0. |
(4.32) |
k=1 |
|
k=1 |
|
Уравнения (4.32) являются первой формой аналитических условий равновесия для плоской системы параллельных сил.
Для равновесия твердого тела под действием плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и сумма моментов относительно любой точки, лежащей на плоскости действия сил, были равны нулю.
F |
|
Y |
|
|
|
|
|
|
|
n |
D |
F |
|
|
|
|
|
||
|
O |
2 |
|
|
C |
|
B |
|
|
|
|
|
||
|
|
|
X |
|
F |
|
|
|
|
|
|
A |
F |
|
3 |
|
|
1 |
|
|
|
|
||
|
Рис. 4.20 |
|
|
|
58
Вторая форма уравнений равновесия для плоской системы параллельных сил не содержит уравнения проекций сил на ось:
n G
∑mA(Fk ) =0;
k=1
n G
∑mB (Fk ) =0.
k=1
При этом предполагается, что точки А, В плоскости ОXY, относительно которых составляются уравнения моментов, не лежат на прямой, параллельной данным силам. Например, прямая АВ не должна быть параллельна оси ОX для сил, изображенных на рис. 4.20.
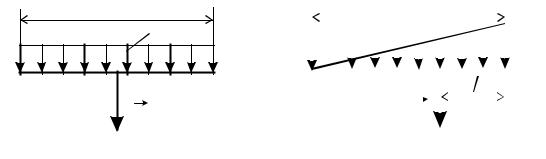
При расчетах иногда встречаются нагрузки, распределенные вдоль поверхности твердого тела по определенному закону.
Равномерно распределенная нагрузка простейший пример распреде-
ленных сил, лежащих в одной плоскости (рис. 4.21, а). Такая система распределенных сил характеризуется постоянной по величине интенсивностью q – значением силы, приходящейся на единицу длины нагруженного участка АВ. Размерность интенсивности нагрузки [q] = F / L , где F – сила, L – длина. Единица измерения интенсивности нагрузки – ньютон на метр (Н/м).
При статических расчетах эту систему параллельных сил можно заменить равнодействующей Q , приложенной в середине отрезка AB = d (рис. 4.21, а), модуль которой
Q =qd. |
(4.33) |
Силы, распределенные вдоль отрезка АВ по линейному закону. Для этих сил интенсивность q является переменной величиной, изменяющейся от нуля до максимального значенияGqmax (рис. 4.21, б).
Равнодействующая Q таких сил равна по модулю площади треугольника АВС
Q = 1 q d. |
4.34) |
||||||||||
2 max |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 4.21
