
Met_913
.pdf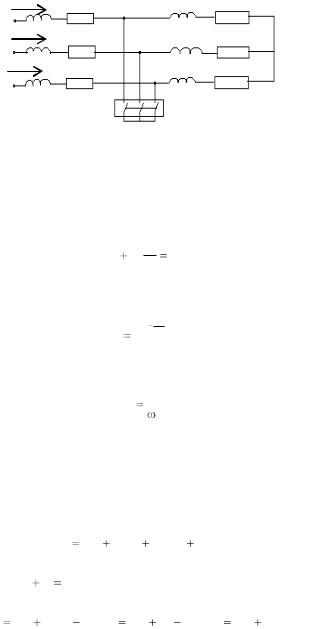
|
|
|
21 |
|
|
|
ic |
|
|
Uc |
L |
rk |
L1 |
r1 |
|
|
ib |
|
|
Ub |
L |
rk |
L1 |
r1 |
|
|
ia |
|
|
Ua |
L |
rk |
L1 |
r1 |
|
|
|
|
B |
Рис. 2. Простая трехфазная цепь
После включения выключателя B цепь распадается на два участка. В правой части цепи после КЗ энергия, запасенная в индуктивности L1, будет переходить в тепло, поглощаясь сопротивлением r1, при этом в дифференциальном уравнении равновесие для каждой фазы участка можно записать так:
di
ir1 L1 dt 0,
его можно решить относительно тока:
t
i i0e Ta1 ,
где Та1 – постоянная времени цепи, она определяется исходя из сопротивлений:
Ta1 |
L |
1 |
|
x1 |
с . |
r |
|
|
r |
||
1 |
1 |
|
|||
В левом участке схемы будет продолжаться переходный процесс за счет имеющегося питания со стороны источника, т. е. в этом участке будет существовать принужденный ток. Он будет сдвинут на некоторый угол относительно предшествовавшего тока.
Дифференциальное уравнение относительно фазы А:
|
|
|
U |
|
i r L |
dia |
|
M |
dib |
|
M |
dic |
, |
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
a |
k |
dt |
|
dt |
|
|
dt |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как ib |
ic –ia , можно записать: |
|
|
|
|
|
|
|
|
|||||||||||||
U |
|
i r L |
dia |
M |
|
dia |
i r (L M ) |
dia |
|
i r L |
dia |
, |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
a |
a k |
|
dt |
|
|
dt |
a k |
|
|
|
|
dt |
a k k dt |
||||||||

22
где Lk = L– M – результирующая индуктивность фазы с учетом влияния других фаз.
В общем виде для любой фазы:
U i r |
L |
di |
. |
(1) |
|
||||
k |
k |
dt |
|
|
Решение уравнения (1) будет:
|
Um |
|
|
|
|
t |
|
|
|
i |
sin( t |
k |
) i |
e Ta , |
(2) |
||||
|
|||||||||
|
Zk |
a (0) |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
где U m – максимальное амплитудное значение фазного напряжения
источника, принимается средним номинальным для ступени КЗ; Zk – полное сопротивление цепи КЗ; ω – угловая частота напряжения источника, определяемая по формуле 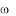 2 f ; t – время; α – фаза воз-
2 f ; t – время; α – фаза воз-
никновения КЗ, фиксирует момент возникновения КЗ (если не задана, можно взять равной нулю); φk – угол сдвига по фазе периодической составляющей тока КЗ относительно напряжения; Та – постоянная времени цепи КЗ:
T |
Lk |
|
xk |
. |
|
|
|||
a |
|
rk |
||
|
rk |
|
||
В уравнении (2) ток i – это сумма двух слагаемых:
1)принужденного тока или периодической слагающей тока КЗ,
2)свободной составляющей или апериодической составляющей тока КЗ.
То есть полный ток КЗ можно записать как:
|
|
|
ikt |
iпt |
iat . |
|
|
|
Начальное значение тока КЗ (t = 0): |
|
|
|
|||||
|
|
|
ik 0 |
iп 0 |
ia 0 |
, |
|
|
отсюда |
|
|
|
|
|
|
|
|
iа (0) |
iк(0) |
iп(0) |
Im(0) sin( |
(0) ) Iпm sin( |
к ), |
(3) |
||
где Im 0 sin( |
– 0 ) |
– |
полный ток |
предшествующего |
режима; |
|||
Iпmsin( – k ) |
– периодическая составляющая тока КЗ; ik 0 |
– началь- |
||||||
23
ное значение Iкз , которое с учетом невозможности изменения тока скачком в цепи с индуктивностью равно i 0 , т. е. току предшеству-
ющего режима в данной фазе к моменту t 0.
На векторной диаграмме [3] ia 0 является проекцией (Im – Iпm )
на ось времени.
В зависимости от фазы включения КЗ начальное значение ia 0 мо-
жет меняться. Его значение будет максимальным, если в момент включения КЗ разность векторов (Im – Iпm ) будет параллельна оси t, т. е.:
1)при α = 0 и отсутствии предшествовавшего тока в цепи,
2)при хk >> rk, то есть когда в цепи преобладает индуктивность,
имеем |
k |
90º , в этом случае будет возникать наибольший аперио- |
|
|
дический ток и будет достигнут максимум мгновенного значения тока КЗ (рис. 3).
Н
орм.
р
ежим
Рис. 3. Изменение полного тока и его составляющих
Максимальное мгновенное значение Iкз называется ударным током iу . Считают, что он наступает примерно через полпериода
(Т/2). При f |
= 50 Гц Т/2 = 0,01 с с момента возникновения КЗ. |
|
||||||||||||
С учетом вышеуказанных условий, т. е. |
|
|
k |
90º и α = 0, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
I |
пm |
I |
пm |
e– 0,01/Ta |
K |
y |
I |
пm |
, |
(4) |
|
|
|
y |
|
|
|
|
|
|
|
||||
Um |
|
|
|
|
|
|
|
|
|
|
|
|
||
где Iпm |
|
|
– амплитуда периодической составляющей тока КЗ |
|||||||||||
|
Zк |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в начальный момент времени; |
|
K y – ударный коэффициент, |
показы- |
|||||||||||

24
вающий превышение ударного тока над амплитудой периодической слагающей Iкз .
Ударный коэффициент в этом случае можно определить по формуле:
K |
y |
1 e–0,01/Ta . |
(5) |
|
|
|
Ударный коэффициент лежит в пределах:
1 Ky 2,
Ky 1 при Та 0 (Lk 0); Ky 2 при Та |
(rk 0). |
Чем меньше Та, тем быстрее затухает ia, следовательно, тем меньше Ky. Влияние ia сказывается лишь в начальный момент переходного процесса, так как в сетях и установках высокого напряжения ia затухает через 0,1–0,3 с, а в установках низкого напряжения она практически незаметна.
При увеличении в цепи доли активного сопротивления, в частности при Х/R < 5 использование формулы (5) для определения ударного коэффициента даст существенную погрешность, поэтому для более точного его определения можно воспользоваться рекомендациями в п. 3.4 или в [1].
2.5. Несимметричные короткие замыкания
2.5.1. Особенности расчета несимметричных коротких замыканий
Метод симметричных составляющих. При расчете трехфаз-
ных КЗ схемы рассматриваются как симметричные, поэтому эквивалентная схема короткозамкнутой цепи представляется в однолинейном изображении, и расчет ведется для одной фазы.
При несимметричном КЗ нельзя вести расчет по одной фазе, так как в сети нарушается симметрия токов в фазах, фазных и линейных напряжений, присутствуют неодинаковые падения напряжений по фазам в элементах системы.
Сравнительно просто несимметричные КЗ и другие режимы в электрических сетях можно рассчитывать с использованием метода симметричных составляющих (МСС). Идея метода симметричных составляющих состоит в следующем: любую несимметричную си-

25
стему трех векторов можно представить в виде трех симметричных систем прямой, обратной и нулевой последовательностей.
Для каждой из этих систем явления, протекающие в различных фазах, подобны, что позволяет:
а) воспользоваться однолинейными схемами для каждой последовательности;
б) вести расчет для одной фазы. Такая фаза называется особой.
Основные положения МСС:
1. Любой из векторов симметричной трехфазной системы можно представить од-
ноименным вектором другой фазы с помощью оператора поворота:
ае j120 .
Умножение вектора на оператор а означает поворот вектора на 120 градусов в положительном направлении (против хода часовой стрелки) (рис. 4). Причем умножение на а2 соответствует повороту на
240 градусов в том же направлении: а |
|
е j 240 . |
|
|
|
||||||||||||||
Сумма операторов поворота: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a2 |
|
a |
|
|
1; |
|
|
|
|
|
|
|
||
их разность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
|
j |
3; |
|
|
|
|
|
|
|||||
а также |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а3 |
|
|
е j 360 . |
|
|
|
|
|
|
|||||
Согласно рис. 4: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
A |
aN |
B |
a2 N |
C |
; |
|
N |
C |
|
|
aN |
A |
a2 N |
B |
; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
N |
B |
aN |
C |
|
a2 N |
A |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
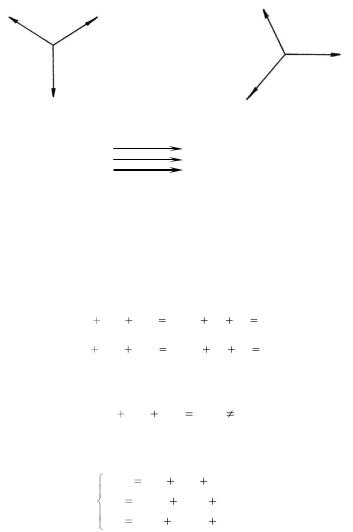
2. Любую несимметричную систему трех векторов можно разложить на три симметричные системы: прямой, обратной и нулевой последовательности (рис. 5).
NA NA1 NA2 |
NA0 ; NB |
NB1 NB2 NB0 ; |
NC |
NC1 NC 2 |
NC0 . |
26
NA1 |
NB1 |
NA2 |
NС2
NС1 |
NВ2 |
а |
б |
|
NA0 |
|
NB0 |
|
NC0 |
|
в |
Рис. 5. Симметричные системы векторов:
а – прямой (чередование векторов то же, что и для основной симметричной системы); б – обратной (чередование векторов противоположно основной симметричной системе); в – нулевой (направление векторов совпадает)
3. Системы прямой и обратной последовательностей являются уравновешенными:
N |
A1 |
N |
B1 |
N |
C1 |
N |
A1 |
(1 a2 |
a) 0 ; |
|||
N |
A2 |
N |
B 2 |
N |
C 2 |
N |
A2 |
(1 a2 |
a) 0 . |
|||
|
|
|
|
|
|
|||||||
Система нулевой последовательности симметрична, но не уравновешена:
NA0 NB0 NC 0 3NA0 0 .
4. Если принять фазу А за особую,
|
NA |
NA1 |
NA2 |
|
NA0 |
|
|
||
N |
В |
а2 N |
A1 |
аN |
A2 |
N |
A0 |
. |
|
|
|
|
|
|
|
||||
N |
С |
аN |
A1 |
а2 N |
A2 |
N |
A0 |
|
|
5. Основное допущение, принимаемое в расчетах несимметричных переходных процессов, заключается в следующем: протекающие токи в схемах замещения разных последовательностей зависят лишь от действующей в схеме разности потенциалов и сопротивления одноименной последовательности (не учитывается взаимоиндукция между фазами).

27
Основные уравнения соотношений между напряжением и током для каждой последовательности имеют вид:
U U U
k1 |
E |
z1рез Ik1 |
k 2 |
0 |
z2рез Ik 2 |
k 0 |
0 |
z0рез Ik 0 |
где Uk1, Uk2, Uk0 и Ik1, Ik2, Ik0 – симметричные составляющие напряжения и тока в месте КЗ; EΣ – результирующая ЭДС прямой последовательности относительно точки КЗ; Z1рез, Z2рез, Z0рез – результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.
Схемы замещения отдельных последовательностей. При расчете любого несимметричного режима или процесса методом симметричных составляющих одной из первоочередных задач является составление схем замещения в общем случае для всех трех последовательностей (прямой, обратной и нулевой). Схемы замещения отдельных последовательностей включают в себя все элементы сети, по которым при данном виде несимметрии протекают токи соответствующих последовательностей. Параметры элементов схем замещения выражают в именованных или в относительных единицах, приводя их соответственно к выбранной за основную ступень напряжения или к выбранным базисным условиям.
Схема прямой последовательности идентична схеме, которую составляют для расчета любого симметричного трехфазногo режима. В зависимости от используемого метода расчета и момента времени
внее вводят генераторы и нагрузки в виде соответствующих сопротивлений и ЭДС. Все остальные элементы отражают на схеме в виде постоянных сопротивлений для момента времени t = 0.
Поскольку пути циркуляции токов обратной последовательности те же, что и токов прямой последовательности, схема обратной последовательности по конфигурации аналогична схеме прямой последовательности. Различие между ними состоит, прежде всего, в том, что
всхеме обратной последовательности ЭДС всех генерирующих ветвей условно считают равными нулю. Кроме того, полагают, что сопротивления обратной последовательности синхронных машин и нагрузок практически постоянны и не зависят от вида и условий возникшей несимметрии, а также от продолжительности переходного процесса.
За начало схемы прямой или обратной последовательности выбирают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей. Это точка нулевого потенциала схе-
28
мы соответствующей последовательности. Концом схемы прямой или обратной последовательности считают точку, где возникла рассматриваемая несимметрия.
Токи нулевой последовательности по существу являются однофазными токами, разветвляющимися между тремя фазами и возвращающимися через землю и параллельные ей цепи. Поэтому токи нулевой последовательности имеют сравнительно небольшую зону прохождения по сети, ограниченную, в частности, обмотками трансформаторов и автотрансформаторов, соединенными в треугольник. Схемы замещения нулевой последовательности по конфигурации сильно отличаются от схем замещения прямой и обратной последовательностей. Началом схемы нулевой последовательности Н0 является точка с нулевым потенциалом, а концом К0 – точка несимметрии.
Схемы замещения нулевой последовательности рекомендуется составлять, начиная от точки, где возникла несимметрия, считая, что в данной точке все фазы замкнуты между собой накоротко и к данной точке приложено напряжение нулевой последовательности. При поперечной несимметрии это напряжение прикладывается относительно земли.
Для случая, когда напряжение нулевой последовательности приложено относительно земли, при отсутствии емкостной проводимости для циркуляции токов нулевой последовательности необходима, по меньшей мере, одна заземленная нейтраль в той же электрически связанной цепи. При нескольких заземленных нейтралях в этой цепи образуется соответственно несколько параллельных контуров для тока нулевой последовательности.
Учет сопротивлений элементов отдельных последователь-
ностей. Все сопротивления, которыми характеризуются отдельные элементы в нормальном симметричном режиме, являются сопротивлениями прямой последовательности. Для элемента, магнитосвязанные цепи которого неподвижны друг относительно друга, сопротивления прямой и обратной последовательностей одинаковы, так как от перемены порядка чередования фаз симметричной трехфазной системы токов взаимоиндукция между фазами элемента не меняется. Таким образом, для трансформаторов, автотрансформаторов, ВЛ, КЛ
и реакторов r1 = r2, x1 = x2.
Реактивное сопротивление обратной последовательности элементов (синхронные генераторы, компенсаторы, двигатели) с вращающимися электромагнитными полями зависит от конструкции машины (симметричности ротора). Токи обратной последовательности образуют магнитный поток, который перемещается относительно статора с синхронной скоростью в обратном направлении. При своем переме-

29
щении этот поток встречает сопротивление в расточке статора, поочередно совмещаясь то с продольной осью ротора, то с поперечной.
Сопротивление обратной последовательности синхронной машины не является в полном смысле постоянным параметром, а может принимать разные значения. Это объясняется магнитной и электрической несимметрией ее ротора и связанным с этим неравенством параметров по продольной и поперечной осям. Следствием магнитной несимметрии ротора является неравенство сопротивлений взаимоиндукции между обмоткой якоря и контурами ротора по продольной и поперечной осям, а следствием электрической несимметрии – неравенство индуктивных сопротивлений рассеяния и активных сопротивлений продольного и поперечного демпферных контуров. Обмотка возбуждения, оказывая влияние только на продольное магнитное поле, увеличивает электрическую несимметрию ротора [1].
Значения реактивного сопротивления обратной последовательности приводятся в каталогах и справочниках как параметры машин. При отсутствии этих данных можно принимать для машин с успокоительными обмотками х2 = 1,22 x"d, а для явнополюсных машин без успокоительных обмоток х2 = 1,45 х'd. В приближенных практических расчетах обычно идут на дополнительное упрощение, полагая для турбогенераторов и машин с продольно-поперечными успокоительными обмотками х2 ≈ x"d. Для асинхронных двигателей сопротивление обратной последовательности можно считать также равным их сверхпереходному сопротивлению х2 = x"d, которое определяется выражением:
|
|
|
X*2 1 / I*пуск , |
|
где I |
|
I пу ск |
– каталожное значение кратности пускового тока |
|
*пу ск |
I ном |
|||
|
|
|||
|
|
|
двигателя по отношению к его номинальному току.
Реактивное сопротивление обратной последовательности обобщенной нагрузки зависит от характера приемников электрической энергии и относительной роли каждого из них в создании нагрузки. Для средней типовой промышленной нагрузки можно полагать, что основная её часть состоит из асинхронных двигателей, реактивное сопротивление обратной последовательности которых практически такое же, как и в начальный момент внезапного нарушения режима,
т. е. х2 = х1 = 0,35 о. е.
Сопротивление нулевой последовательности элементов резко отличается от сопротивлений прямой и обратной последовательностей, поскольку взаимоиндукция при этом сказывается иначе. Кроме того, реак-
30
тивное сопротивление нулевой последовательности зависит от схемы соединения фаз рассматриваемого элемента и схемы заземления нейтрали. Если пути для прохождения токов нулевой последовательности нет, то это равносильно сопротивлению в цепи, равному бесконечности.
В синхронных машинах с заземленной нейтралью протекают токи нулевой последовательности, которые создают одинаковые по значению и совпадающие по времени магнитные потоки. Поскольку фазовые обмотки машины сдвинуты по окружности статора на 120º, магнитные потоки нулевой последовательности машины будут сдвинуты в пространстве друг относительно друга также на 120º. Поэтому можно считать, что результирующий магнитный поток нулевой последовательности в расточке машины равен нулю и реакции ротора не вызывает.
Реактивное сопротивление нулевой последовательности синхронных машин определяется рассеянием магнитного потока в пазах и лобовых частях, причем по значению оно меньше, чем при симметричном трехфазном потоке. Это уменьшение зависит от типа обмотки, из-за чего реактивное сопротивление синхронных машин колеблется в широких пределах: x0 = (0,15 ÷ 0,6) x"d.
Если нейтраль генератора изолированная, то токи нулевой последовательности в нем не протекают (х0 = ∞) и в эквивалентную схему нулевой последовательности такой генератор не вводится.
Основные нагрузочные ответвления, как правило, работают с изолированной нейтралью, так что пути для токов нулевой последовательности здесь нет. По этой причине можно считать, что реактивное сопротивление нулевой последовательности нагрузочных ответвлений равно бесконечности и вносить их в эквивалентную схему нулевой последовательности не требуется.
Реактивное сопротивление реакторов в основном определяется их самоиндукцией. Если речь идет о взаимоиндукции, то она играет меньшую роль в создании общего реактивного сопротивления реактора из-за большого расстояния между катушками. С учетом этого реактивное сопротивление нулевой последовательности реактора можно полагать равным сопротивлению прямой последовательности.
Реактивное сопротивление нулевой последовательности ВЛ зависит от её конструктивных особенностей (одноцепная, двухцепная, наличие или отсутствие проводящего стального троса). Расчетные выражения для x0 в каждом случае берутся из справочника.
Сопротивление нулевой последовательности КЛ зависит от типа кабеля, способа его прокладки, параметров оболочки кабеля и характера её заземления, параметров заземлителей и т. п. Основной путь для протекания (возвращения) тока нулевой последовательности – оболочка или броня кабеля.
