7. Высшие гармоники в трехфазных цепях.

В трехфазных цепях кривые напряжения фаз B и C обычно воспроизводят форму кривой фазы A.

U_А=f(t)

U_B=f(t-T/3)

U_C= f(t+T/3)

Рассмотрим гармоники K-ого порядка во всех трех фазах:

U_АK=U_KMsin(Kωt+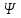_K)

ωt=2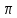

U_BK= U_KMsin(Kωt+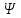_K-)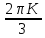

U_CK=U_KM(Kωt+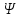_K+)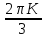

Следов-но напряж. гармоник,порядка кратного 3, K=3n n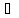Z во всех фазах в момент времени имеет одно и тоже значение и направление

при K=3n+1 гармоники трех фаз образуют симметрич. сис-му U последовательность которых совпадает с последовательностью фаз первой гармоники.

при при K=3n+2 гармоники трех фаз образуют симметрич. сис-му U последовательности обратной основной.

Таким образом гармоники порядка 1,4,7,10 обр-т сис-му U прямой последовательности

гармоники порядка 2,5,8,11 обр-т сис-му U обратной последовательности

гармоники порядка 3,6,9,12 обр-т сис-му напряжений нулевой последовательности

При наличии постоянной составляющей в напряжении каждой из фаз она может рассматриваться как нулевая гармоника порядка кратного 3,т.е. образующая нулевую последовательность.

Если фазы генератора соединены звездой, то при несинусоид. фазном U, линейные U не содержат гармоник порядка кратных 3,т.к. они образуют сис-мы нулевой послед-ти.

U_ф=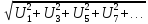

U_Л=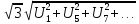

U_Л< U_ф*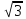

Ток в нейтральном проводе

I_N=3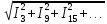

n=3*1 n=3*3 n=3*5

При отсутствии нейтральн. провода токи в каждой из фаз не могут содерж. высших гармоник порядка кратного 3.

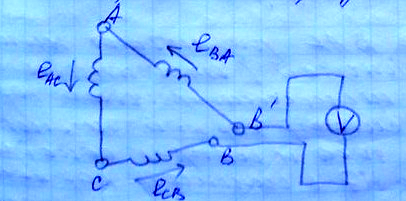
Если фазы генератор. соеденин. треу-ком, то при несинусоид. ЭДС,сумма ЭДС,действ. в замкн. контуре генератора не равно 0,а равна 3-ой сумме высших гармоник, порядка, кратного 3.

Вольтметр измерит гармоники ЭДС ,порядка кратн. 3 т.к. остальные в сумме дадут 0.

U=3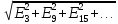

ЭДС гармон. порядка кратн. 3 вызыв. внутренний ток в генераторе.

Фазное U линейному

U_ф=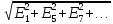I_Ф=3

Линейный ток во внешней цепи.

I_л=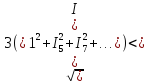I_Ф*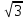

Открытый треугольн. с ЭДС содерж. высшие гармоники примен. как утроитель частоты во внешн. цепи,подключ. к генератору обмотки кот. соедин. треугольн. токи не содержат гармон. порядка кратного 3.

IV. Цепи (линии) с распределенными параметрами.

1. Направляющие сис-мы передачи электроэнергии и их модели.

Электротехн. устр-ва предназн. для выработки и преобразов. эл. энергии. Электрические сигналы служащие носителями энергии необходимо передавать от одного устр-ва к другому из одной области простр. в другую. Для этого служат различные виды передающих сис-м:

1)Радиоприемник(передача электр. волн в неогран. среде)

2)Направляющие линии передач

3)В электроэнергетики используют проводные линии передачи низкой промышл. частоты

4)В информационных сис-х применяют оптические и диэлектрические волноводы, кабельные и проводниковые линии связи.

Решение задачи распространения электром. энергии по направл. сис-м базируется на ур-нях электродинамики(ур-е Максвела).

В диапазоне работы большинства пром. линий связи при частотах f<10⁸ Гц в основном справедливо квази-статическое приближение и можно использовать эквивалент. электр. схемы.

В проводных линиях связи длина линии может быть соизмерима с длиной волны, но поперечные размеры линии существ. меньше в таких линиях токи и напряжения для одного и того же момента времени различн. в разных сечениях и необходимо учитывать изменение их значения вдоль линии.

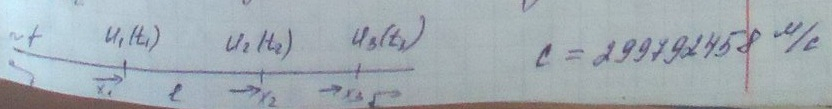
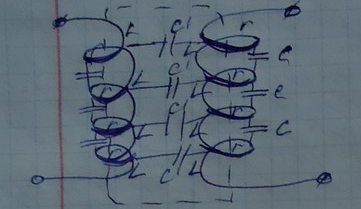
К распредел. цепям относятся не только проводн. линии,но и электротехнические устройства ,в которых требуется учитывать распределение U и I вдоль координат,например многоветк. обмотки эл. машины.

Обмотку трансформатора можно считать цепью с распред. параметрами только при большой частоте прилож. U либо импульса U.Ток в такой цепи изменяется по длине обмотки от витка к витку и ее следует рассматривать как эл. цепь с распредел. вдоль цепи продольн. и поперечными сопротивл.

Цепью с распредел. параметрами называют устр-во,в котором величина тока или магнитного потока изменяется вдоль длины и зависят от двух переменных времени и расстояния.

Любые электр. и магнитн. цепи с распредел. параметрами могут быть нелинейн. и линейн. однородн. и неоднородн.i(t,e), Ф(t,e), U(t,e)

Однородной называют цепь с распределительными параметрами при условии, что одинаковые все продольные U и поперечные проводимости идентичных участков устройства.

Электрические линии связи и передача электроэнергии имеют различные конструктивные исполнения:

1)Коаксиальный кабель 2)Триоаксиальный кабель 3)Плоский многожильный кабель

4)Многопроводная ВЛ связи 5)Трехфазная линия электропередачи энергии