
- •I. Четырехполюсники.
- •1. Основные определения и классификация четырехполюсников.
- •2. Системы уравнений четырехполюсников.
- •3. Входное сопротивление четырехполюсника при произвольной нагрузке.
- •4. Соединения четырехполюсника.
- •II. Переходные процессы в электрических цепях.
- •6. Переходные процессы в rLc цепи(последовательном контуре).
- •7. Общий случай расчета переходных процессов классическим методом.
- •8. Основные положения операторного метода расчета переходных процессов в электрических цепях.
- •9. Изображение напряжения на индуктивности.
- •11. Закон Ома в операторной форме. Внутренние эдс.
- •12. Первый закон Кирхгофа в операторной форме
- •13. Второй закон Кирхгофа в операторной форме
- •12. Первый закон Кирхгофа в операторной форме.
- •14. Расчет переходных процессов операторным методом в rc контуре при ступенчатом воздействии.
- •13. Второй закон Кирхгофа в операторной форме.
- •15. Расчет переходных процессов операторным методом в параллельном колебательном контуре при ступенчатом воздействии.
- •16. Расчет переходных процессов операторным методом в параллельном колебательном контуре при гармоническом воздействии
- •17. Последовательность расчета пп операторным методом
- •18. Расчет переходных процессов методом переменных состояния.
- •19. Последовательность расчета переходных процессов методом переменных состояния.
- •20. Численный метод решения уравнений состояния динамической цепи.
- •III. Периодические несинусоидальные токи в электрических цепях.
- •1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.
- •2. Действующие и средние значения несинусоидальных электрических величин.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •3. Активная мощность при несинусоидальных напряжении и токе.
- •4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
- •5. Несинусоидальные кривые с периодической огибающей. Биения
- •7. Высшие гармоники в трехфазных цепях.
- •IV. Цепи (линии) с распределенными параметрами.
- •1. Направляющие сис-мы передачи электроэнергии и их модели.
- •2. Уравнение двухпроводной линии
- •3.Уравнения многопроводных линий
- •4.Расчет процессов в цепях с распределенными параметрами.
- •5.Установившиеся режимы в линиях.
- •V. Нелинейные электрические цепи.
- •1. Нелинейные элементы и их вольтамперные характеристики.
- •2. Последовательное соединение нелинейных элементов.
- •3. Параллельное соединение нелинейных элементов.
- •4. Смешанное соединение нелинейных элементов.
- •5. Статические и дифференциальный сопротивления.
- •6. Замена нелинейного элемента линейным сопротивлением и эдс.
- •VI. Магнитные цепи.
- •2. Закон Ома и законы Кирхгофа для магнитных цепей.
- •3.Расчет неразветвленных магнитных цепей.
- •4. Расчет разветвленных магнитных цепей.
- •5. Магнитные цепи переменного тока.
- •VII. Теория электромагнитного поля.
- •1. Электромагнитное поле и его уравнение в интегральной форме.
- •2. Закон полного тока в дифференциальной форме (первое уравнение максвелла )
- •3. Закон электромагнитной индукции в дифференциальной форме(второе уравнение максвелла)
- •4. Теорема гаусса и постулат максвелла в дифференциальной форме
- •5. Выражение в дифференциальной форме принципов непрерывности магнитного потока и непрерывности электрического тока.
- •8. Уравнение Пуассона и Лапласа для электростатического поля
- •9. Уравнение Максвелла в комплексном виде. Волновое уравнение Гельмгольца
- •11. Вектор Пойнтинга
- •12. Вывод волновых уравнений непосредственно из уравнений Максвелла в дифференциальной форме
- •10. Основные свойства плоских электромагнитных волн
- •13. Численные методы расчета электромагнитных полей. Граничные условия
5. Несинусоидальные кривые с периодической огибающей. Биения
Это кривые, относящиеся к классу почти периодических. Они также разлагаются на гармонические составляющие. Период таких кривых обычно во много раз превышает период любой из составляющих и может стремиться к бесконечности. К числу явлений, характеризуемых такими кривыми, относятся биения и модуляции.
Биения. Простейший
случай получается при сложении двух
синусоид с равными амплитудами, но не
равными частотами ω1 и ω2, причем ω1 >
ω2:![]()
Преобразуя сумму
синусов, получим![]()
Можно считать, что
кривая f(t) представляет собой синусоиду
с угловой частотой![]() амплитуда которой изменяется по
косинусоиде со значительно меньшей
угловой частотой
амплитуда которой изменяется по
косинусоиде со значительно меньшей
угловой частотой![]() ,
тогда
,
тогда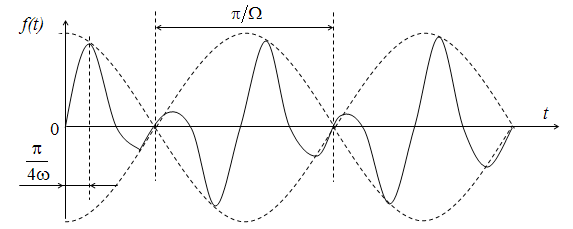
![]()
Частотой биений -
частота![]() ,
равная числу максимумов огибающей
кривой в единицу времени.
,
равная числу максимумов огибающей
кривой в единицу времени.
Пример несинусоидальной кривой с периодической огибающей показан на рис.1.
Период биений![]() в
общем случае не равен периоду кривой
f(t).
в
общем случае не равен периоду кривой
f(t).
Модулированные
колебания. Синусоидально изменяющаяся
величина f(t) =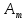 sin(ω
t + Ψ) задается тремя параметрами:
амплитудой
sin(ω
t + Ψ) задается тремя параметрами:
амплитудой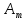 ,
угловой частотой ω и начальной фазой
Ψ. Эти величины не зависят от времени.
Однако для передачи различного рода
сигналов применяются генераторы, в
которых одна из этих величин изменяется
по некоторому заданному закону. Изменение
во времени одного из параметров
,
угловой частотой ω и начальной фазой
Ψ. Эти величины не зависят от времени.
Однако для передачи различного рода
сигналов применяются генераторы, в
которых одна из этих величин изменяется
по некоторому заданному закону. Изменение
во времени одного из параметров ,
ω или Ψ называют модуляцией. Различают
амплитудную, частотную и фазовую
модуляции.
,
ω или Ψ называют модуляцией. Различают
амплитудную, частотную и фазовую
модуляции.
Пусть функция,
изменяющаяся с частотой
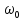 и амплитудой
и амплитудой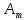 (t), модулирована гармоническим сигналом
с частотой Ω <
(t), модулирована гармоническим сигналом
с частотой Ω <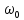 относительно среднего значения
относительно среднего значения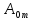 ,
т.е. с законом изменения
,
т.е. с законом изменения (t) (рис.8.2):
(t) (рис.8.2):
![]()
Частота
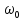 называется несущей частотой, частотаΩ
– модулирующей частотой, m
– коэффициентом модуляции.
называется несущей частотой, частотаΩ
– модулирующей частотой, m
– коэффициентом модуляции.
При определении
токов или напряжений модулированные
по амплитуде колебания могут быть
разложены на синусоидальные составляющие:
![]()
Тогда
![]() ,
где
,
где![]()
![]() ;
;![]()

Таким образом,
простейшие модулированные по амплитуде
колебания могут быть представлены в
виде суммы трех синусоидальных колебаний
с несущей частотой
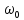 ,
боковыми частотами
,
боковыми частотами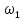 ,
, и постоянными амплитудами.
и постоянными амплитудами.
Под действующим
значением колебаний с периодической
огибающей, описываемых функцией![]() ,
обычно понимают действующее значение
огибающей, деленное на
,
обычно понимают действующее значение
огибающей, деленное на![]()
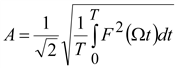 ,
где T
= 2π/Ω.
,
где T
= 2π/Ω.
Этим выражением можно пользоваться, если исследуется непериодический процесс за достаточно больной промежуток времени
.
|
6.Резонанс в цепи несинусоидального тока. |
|
В цепях несинусоидального тока резонансные режимы возможны для различных гармонических составляющих. Как и при синусоидальных токах, резонанс на к-й гармонике соответствует режиму работы, при котором к-е гармоники напряжения и тока на входе цепи совпадают по фазе, иначе говоря входное сопротивление (входная проводимость) цепи для к-й гармоники вещественно. Пусть имеет место цепь на рис. 1,а, питающаяся от источника несинусоидальной ЭДС, в которой емкость конденсатора может плавно изменяться от нуля до бесконечности.
Для
к-й гармоники тока можно записать
Таким
образом, при изменении С величина к-й
гармоники тока будет изменяться от
нуля при С=0 до
Следует
отметить, что, несмотря на то, что
обычно с ростом порядка гармонической
ЭДС ее амплитуда уменьшается, в режиме
резонанса для к-й гармонической ее
значение
Резонансные явления используются для выделения гармоник одних частот и подавления других. Пусть, например, в цепи на рис. 2 необходимо усилить q-ю гармонику тока на нагрузке и подавить р-ю.
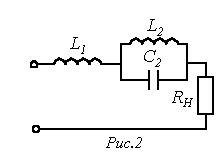
Для
подавления р-й гармоники в режим
резонанса токов настраивается контур
Для выделения q-й гармоники вся цепь для нее настраивается в режим резонанса напряжений:
Отметим, что рассмотренные явления лежат в основе работы L-C -фильтров.
|

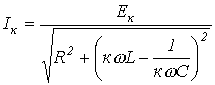 ,где
,где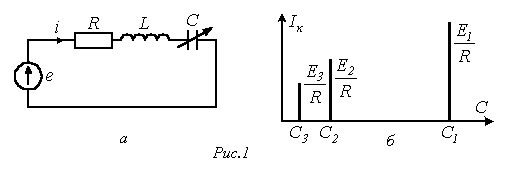
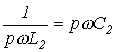 .
.
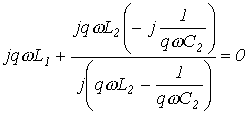 ,откуда
при известных
,откуда
при известных
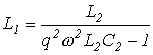 .
.