2. Действующие и средние значения несинусоидальных электрических величин.

Измерительные приборы тепловой, эл.магнитной, эл.динамической, эл.статической систем показывают действующие значения измеряемых величин. Действующие значение несинусоидальных ЭДС (напряжения и тока), равно среднеквадратичному её значению за время равное её периоду:

; ;;

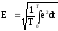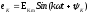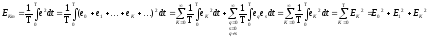При ;

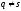
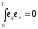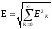- аналогично для действительных значений тока и напряжения:

_{; ;}

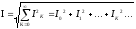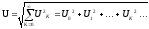Действующее значение несинусоидальной величины равно корню квадратному из суммы квадратов действующего значения и действующих значений её гармоник .

Эквивалентной синусоидальной величиной называют такую величину действующего значения, которая равна действующему значению несинусоидальной величины. Амплитуда эквивалентной синусоидальной ЭДС определяется выражением: ;

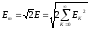Среднее значение за полупериод: .

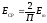4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.

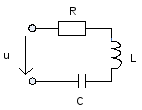
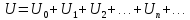
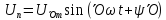
Так как цепь линейна то можно найти составляющую тока создаваемую каждой составляющей U –нием ,а суммарный ток найти сложением составляющих токов используя принцип наложения.

Постоянное состояние I не синусоидального тока может существовать только тогда ,когда в цепи нет C конденсатора.

Гармоника – порядка определиться: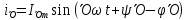

,

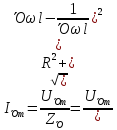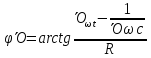
Далее по принципу:

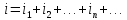
Полное сопротивление цепи для любой гармоники I зависит от порядка гармоники

, ;

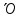
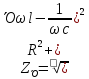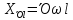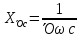
3. Активная мощность при несинусоидальных напряжении и токе.

Активная мощность определяется как средняя мощность за период.

; ;

;

; ;

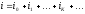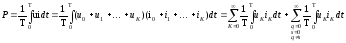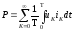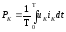Для активной мощности при несинусоидальном напряжении выражение представляет из себя сумму активной мощности каждой гармоники в отдельности.

;;

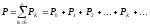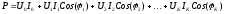К эл.цепям с несинусоидальными напряжением и током применимо понятие полной мощности, определяемой произведением действующих значением напряжения и тока S=UI.

;-коэффициент мощности для несинусоидальных напряжений и тока, Р-активная мощность, S-полная мощность.

В отличие от эл.цепей синусоидального тока где коэффициент мощности цепи с активным сопротивлением равным 1, в цепях несинусоидальных напряжений и тока 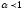, даже для цепи с активным сопротивлением, зависящим от частоты и тока.

Допустим что ток в цепи синусоидальный, а ток содержит высшие гармоники:;;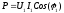

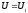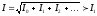
Действующее значение напряжения: ;

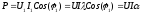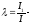коэффициент искажения.

Так как 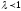, то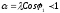, в любом случае из этого следует что наличие высших гармоник в напряжении и токе почти всегда приводит к уменьшению коэффициента мощности, при замене несинусоидальных напряжений и тока эквивалентными величинами сдвиг фаз между ними определяется коэффициентом мощности -..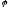

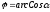4. Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.

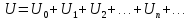
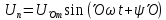
Так как цепь линейна то можно найти составляющую тока создаваемую каждой составляющей U –нием ,а суммарный ток найти сложением составляющих токов используя принцип наложения.Постоянное состояние I несинусоидального тока может существовать только тогда ,когда в цепи нет C конденсатора.

Гармоника 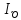– порядка определиться:,

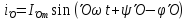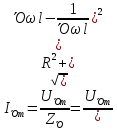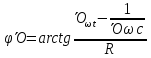, ,Далее по принципу:

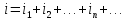
Полное сопротивление цепи для любой гармоники I зависит от порядка гармоники :

, ;
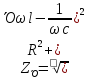
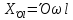